В статье приведена упрощенная математическая модель. Представлен набор программных модулей. Создана имитационная модель в среде Anylogic. Приведены результаты работы.
Ключевые слова: подвеска, демпфирование, имитационное моделирование, математическая модель, накопитель, функция, динамическая переменная.
The article presents a simplified mathematical model, describes the algorithms implemented in the simulation model. A simulation model has been created in the Anylogic environment. The results of the work are presented
Keywords: suspension, damping, simulation, mathematical model, accumulator, function, dynamic variable.
Проблематика создания колебательной системы для автотранспортного средства, наглядно продемонстрирована компанией «Яндекс» при создании «Яндек.Ровера». Разработкой данного аппарата компания начала заниматься в июне 2019 года. Механизированная платформа Яндекса является роботом курьером, который представляет из себя самодвижущуюся тележку с шестью колёсами. Над тележкой располагается отсек с множеством датчиков для анализа окружения и отсеком для груза (Рис.1). В ноябре 2019 года Яндекс представил первый образец данного проекта.

Рис. 1. Робот курьер «Яндекс.Ровер»
Для создания первого прототипа использовались 8-дюймовые колёса и драйвера от гироскутеров, плата для разработчиков Nucleo [1]. Корпус собирался из фанеры и алюминиевых профилей. Прототипом же было выбрано шестиколёсное шасси, управляемое с пульта. Прошивка для драйверов модифицировалась под свои задачи, а команды управления рассылались помощью Nucleo.
В целом платформа доказала, что пригодна для использования в прототипе: она была достаточно грузоподъёмной и быстрой. Но тесты показали, что жёстко закреплённые колёса не подходят для городских условий: на неровностях шасси начинало поворачивать непредсказуемо, из-за того, что не все колёса касаются земли. Было принято решение добавить балансирную подвеску передних двух осей и дополнительно загрузить среднюю ось с помощью пружин, чтобы робот поворачивал преимущественно вокруг центра средней оси. Для проверки стабильности работы колебательной системы было необходимо создать стенд для экспериментов, который показан ниже на рисунке 2.

Рис. 2. Стенд для проверки стабильности работы колебательной системы
Для того, чтобы упростить процесс разработки и довести подвеску до рабочего состояния в кратчайшие сроки предлагается использовать специализированное программное обеспечение — имитационной моделью подвески робототехнического устройства, описание которой представлено ниже.
Математическая модель
Интерфейс, с помощью которого осуществляется оперативное управление параметрами тележки и дороги, изображён на рисунке 3.
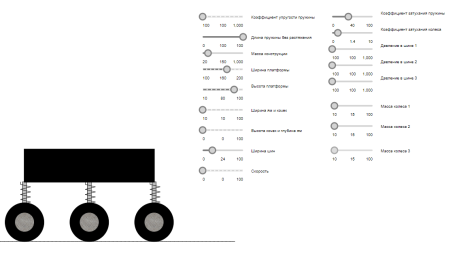
Рис. 3. Интерфейс программы в среде Anylogic
Предполагается, что колеса и собственно платформа могут перемещаться только по вертикальной оси, а по горизонтальной оси перемещается бесконечная дорога с заданным профилем. Скорость перемещения дороги также можно изменять с помощью полузнка.
Для вычисления смещения центра тяжести платформы используется закон Ньютона:
|
m p y’’=m p g-F 1 -F 2 -F 3 |
(1) |
где F i — сила, действующие со стороны пружин подвески, m p g — сила тяжести. В данной модели вращение платформы относительно центря масс не учитывается. На колеса платформы также действуют силы тяжести, силы реакции опоры и силы со стороны подвески:
|
m wi y’’=m wi g+F 1 +F 2 +F 3 -N i; i=1,2,3 |
(2) |
Силы, действующие на платформу и на колеса, определяются действием пружин по закону Гука с коэффициентом жесткости K и коэффициентом демпфирования — B. Силы реакиции со стороны дорожного покрытия определяются “глубиной погружения шины колеса в профиль дороги” (таким образом моделируется деформация шины колеса) и приведенным давлением в шине колеса (аналог коэффициента жесткости). Для колеса также учитываются энергетические потери при движении путем задания коэффициента демпирования. Все параметры, включая размер колес и толщину шины, могут быть изменены пользователем с помощью соответствующего ползунка в интерфейсе программы.
Предложенные уравнения движения являются основой для создания программного обеспечения, позволяющего исследовать математическую модель и проверить её адекватность.
Разработка программы
Для создания имитационной модели трёхосной подвески автотранспортного средства в среде Anylogic необходимы, задать параметры для констант, динамические переменные для работы данных со временем и накопители для реализации в данной среде дифференциальных уравнений
Накопитель может брать производные формул, состоящие из параметров и динамических переменных. Для того, чтобы взять вторую производную из формулы, необходимо занести в заранее созданный накопитель, накопитель, в котором взята первая производная. На рисунке 2 VY_Wheel1 берет производную из формулы, которая является формулой ускорения для колеса, а накопитель Y_Wheel1 берет производную из VY_Wheel1. Из этого выводится координата Y колеса, имеющая скорость и ускорение.
Для взаимосвязи динамических переменных, параметров и накопителей используются связи. Они задаются после задания в соответсвующем накопителе дифференциального уравнения или при задаче параметра в динамической переменной. Примеры связей приведены на рисунке 4.
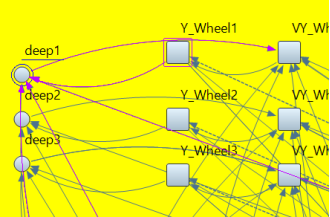
Рис. 4. Связи участвующие при расчете заглубления колеса
Для создания модулей инициализации, модулей расчетов координат точек и других модулей операций, которые не участвуют в математической модели используются функции. Чтобы функция стала динамической необходимо добавить её в динамическую переменную.
Итоговый набор программных модулей продемонстрирован на рисунке 5.
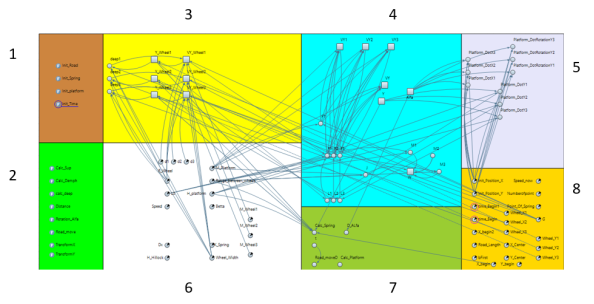
Рис. 5. Итоговый набор программных модулей.
На данном рисунке продемонстрированы следующие программные модули.
1– модуль инициализации;
2 — модуль вычислений;
3 — модуль динамики колёс;
4 — модуль динамики платформы модуль;
5 — модуль динамических переменных для привязки координат;
6 — модуль, содержащий входные данные модуль динамических;
7 — модуль динамических переменных для привязки функций расчёта;
8 — модуль параметров, которые не вводятся пользователем.
Результат работы
Далее представлены результаты работы программы в виде временных графиков (Рис.5–7). При следующих параметрах подвески.
Масс платформы — 150 кг.
Масс одного колеса — 15кг
Стартовая длина пружины подвески — 0.18м
Высота неровностей — 0м
Давление в одной шине — 100 кПа
Коэффициент затухания колеса — 1.4
Коэффициент затухания пружины — 40
Упругость пружины — 0.1 Н/м
Интервал времени, на котором рассматривается модель — 100с
Скорость — 0 м/с
A)
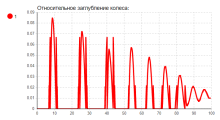
C)
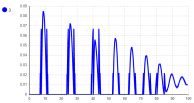
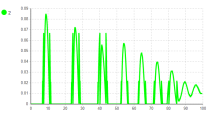
Рис. 6. Набор временных графиков относительного заглубления колеса: A — Колесо 1, B — Колесо 2, С — Колесо 3
A)
C)
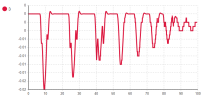
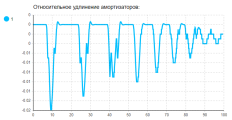
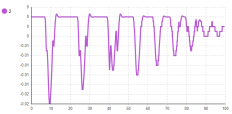
Рис. 7. Набор временных графиков относительного удлинения амортизаторов: A — Амортизатор 1, B — Амортизатор 2, С — Амортизатор 3
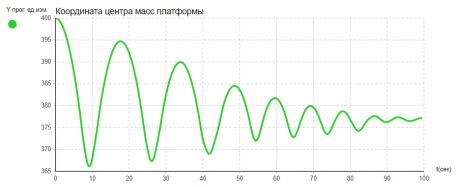
Рис. 8. Временной график координаты центра масс платформы
Следует уточнить, что стартовая точка платформы расположена выше точки дороги. В связи с падением платформы на дорожное полотно и возникают первичные колебания (рис. 8). Затухание колебаний свидетельствует о корректной работе демпфирующей силы. Так как вращение платформы не учтено, все колёса касаются дорожного полотна в один момент, что отображается на графиках рисунка 6. Относительные удлинения амортизаторов также идентичны (рис. 7).
По итогу реализована программная среда, для анализа поведения подвески трехосного автотранспортного средства, с возможностью оперативно изменять параметры. Данная программа в дальнейшем сможет быть улучшена за счет технологии открытого доступа.
Литература:
- Встречаем ровер третьего поколения: история создания робота-курьера Яндекса [Электронный ресурс] URL:https://habr.com/ru/company/yandex/blog/590997/







