Показано, что случайные погрешности в данных об ускорении датчика представляют собой нормальный случайный процесс со среднеквадратичным отклонением менее 0,5 %.
Ключевые слова: измерение ускорений, интегральные акселерометры, датчики в смартфонах.
Все современные смартфоны содержат датчики ускорений для обнаружения своих движений. Интересна возможность их использования в задачах прогнозирования землетрясений [1]. Целью данной работы было определение случайных погрешностей одного из таких датчиков. Датчик MPU-9250 [2] измеряет ускорение, включая в него ускорение силы тяжести (гравитацию). Было проведено 6 опытов, в которых одна из осей датчика была направлена вертикально вниз или вверх. При этом датчик закрепляли неподвижно. В каждом опыте проводили регистрацию 1000 точек данных. Результаты обработки данных приведены в табл. 1, 2 и на рис. 1–3.
Таблица 1
Средние значения данных от датчика
|
Ориентация |
Среднее sx |
Среднее sy |
Среднее sz |
|
Ось X вертикально вверх |
2066,3 |
-22,6 |
-107,2 |
|
Ось X вертикально вниз |
-2036,5 |
-2,8 |
-162,0 |
|
Ось Y вертикально вверх |
-24,2 |
2043,4 |
-120,2 |
|
Ось Y вертикально вниз |
-11,5 |
-2067,6 |
-91,3 |
|
Ось Z вертикально вверх |
-56,4 |
3,8 |
2011,2 |
|
Ось Z вертикально вниз |
32,1 |
-43,0 |
-2210,3 |
Таблица 2
Среднеквадратичные отклонения от средних значений
|
Ориентация |
СКО sx |
СКО sy |
СКО sz |
|
Ось X вертикально вверх |
8,3 |
6,0 |
7,3 |
|
Ось X вертикально вниз |
5,2 |
7,5 |
9,4 |
|
Ось Y вертикально вверх |
4,8 |
6,7 |
7,3 |
|
Ось Y вертикально вниз |
6,5 |
7,0 |
10,1 |
|
Ось Z вертикально вверх |
7,0 |
6,6 |
9,3 |
|
Ось Z вертикально вниз |
5,2 |
5,6 |
9,5 |
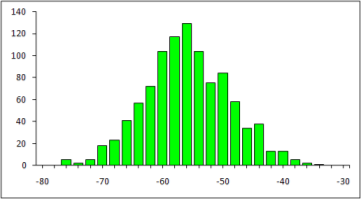
Рис. 1. Гистограмма сигнала sx
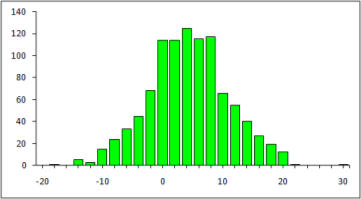
Рис. 2. Гистограмма сигнала sy
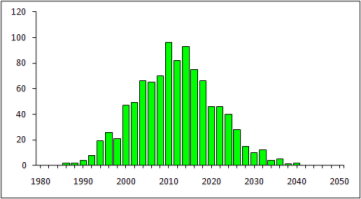
Рис. 3. Гистограмма сигнала sz
Проверку гипотезы о нормальности распределения случайных погрешностей проводили по критерию Колмогорова [3] на выборке из 1000 измерений, по которым были построены показанные выше гистограммы. Был принят уровень значимости 0,05 и поэтому критическое значение критерия Колмогорова составило 0,886/
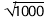
Были построены выборочные распределения
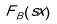
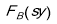
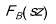
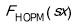
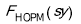
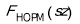
Таблица 3
Результаты проверки нормальности распределения
|
Ось |
sx |
sy |
sz |
|
Максимальное абсолютное отклонение от нормального распределения |
0,0216 |
0,0172 |
0,0112 |
|
Критическое значение |
0,028 |
0,028 |
0,028 |
|
Соответствует критерию Колмогорова |
да |
да |
да |
Таким образом, можно сделать вывод, что случайные погрешности датчика подчиняются нормальному распределению вероятностей. Для примера на рис. 4 приведены распределения
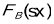

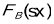

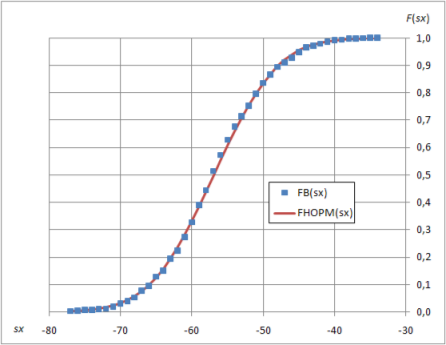
Рис. 4. Выборочное и теоретическое нормальное распределения случайных погрешностей
Литература:
- Kong Q., Lv Q., Allen R. M. Earthquake early warning and beyond: Systems challenges in smartphone-based seismic network [Электронный ресурс] / Proceedings of the 20th International Workshop on Mobile Computing Systems and Applications. — 2019. — P. 57–62. — URL: https://arxiv.org/pdf/1901.06614.pdf (дата обращения: 15.03.2022).
- MPU-9250 Product Specification. Revision 1.1 [Электронный ресурс] / InvenSense, Inc. — URL: https://invensense.tdk.com/wp-content/uploads/2015/02/PS-MPU-9250A-01-v1.1.pdf (дата обращения: 10.03.2022).
- Орлов, А. И. Прикладная статистика. Учебник [Текст]. — М.: Экзамен, 2009. — 671 с.







