В статье автор приводит математическую модель, которая позволит выбрать оптимальный с точки зрения максимизации прибыли вариант производства и реализации продукции.
Ключевые слова: стратегическое развитие, строительная отрасль, оптимизация прибыли.
На современном этапе развития строительной отрасли в организациях не уделяется должного внимания разработке долгосрочных стратегических программ развития, системному поиску прорывных технологий, использованию на требуемом уровне научного обеспечения производства. В результате этого система управления не соответствует требованиям рыночной экономики, а строительные организации несут потери из-за отсутствия оптимальной экономической политики. В соответствии с данной проблемой целесообразным является разработка универсальной математической модели, которая позволит выбрать оптимальный с точки зрения максимизации прибыли вариант производства и реализации продукции.
Исходными данными для построения экономико-математической модели являются нормативы и прогнозируемые результаты внедрения предлагаемых направлений экономической политики, их влияние на издержки производства.
Для формализации задачи введём следующие обозначения:
i =
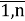
x i — искомый объем производства i-го ресурса;
X 1 х n — вектор-строка производства ресурсов по видам;
O i H — остаток i-го вида ресурса на начало производственного цикла (в нат. ед. изм.);
O H 1 x n = (O i H , i =
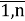
O i K — остаток i-го вида ресурса на конец производственного цикла (в нат. ед. изм.);
O
K
1
x
n
= (O
i
K
, i =
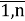
j=

z j — искомый объем производства j-го конструктивного элемента (в нат. ед. изм.);
Z
1
x
m
= (z
j
, j=

Q j H — остаток у — го вида конструктивных элементов на начало производственного цикла (в нат. ед. изм.);
Q H 1 x m = (Q j H , j=

Q j K — остаток j-го вида конструктивных элементов на конец производственного цикла (в нат. ед. изм.);
Q
K
1
x
m
= (Q
j
K
, j=

a ji — норма расхода на производство j-ой единицы конструктивного элемента i-го вида ресурса (в нат. ед. изм.);
A
m
x
n
= (a
ji
, j=

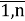
l =
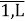
y l — искомое количество произведённых зданий l-го типа;
Y
1
x
L
= (y
l
, l =
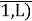
b lj — норматив расхода на l-ый тип здания j- го конструктивного элемента (в нат. ед. изм.);
B
L
x
m
= (b
lj
, l =
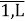

h=
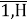
S lh — средняя общая площадь h-тых квартир в l-ом доме, в м 2 ;
S
L
x
H
= (S
lh
, l =
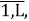
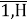
Д спрос 1хн — вектор спроса на площадь квартир h-го типа;
d h — доля строительного предприятия на рынке в производстве квартир h-го типа;
d
Hx
1
= (d
h
, h=
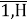
⍺ h , β h — соответственно минимальная и максимальная доля рыночного спроса на квартиры h-го типа.
t ( p ) i — норматив трудоёмкости изготовления единицы натурального объёма i-го вида ресурса, в чел.-час.;
T
(
p
)
n
x
1
= (t
(
p
)
I
, i =
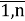
t ( K ) j — норматив трудоёмкости изготовления единицы натурального объёма j-го вида конструктивных элементов, в чел.-час.;
T ( K ) m x 1 = (t ( K ) j , j=

t (з) j — норматив средней трудоемкости возведения j-го конструктивного элемента, в чел.-час.;
T
(з)
m
x
1
= (t
(з)
j
, j=

1 этап. Определение потребности в видах конструктивных элементов для производства искомого количества зданий:
W
1 x
m
(Y) = Y
1 x
L
* B
L x
m
; w
j
=
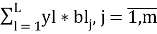
2 этап. Определение потребности в видах ресурсов для производства искомого количества зданий:
V
1 x
n
(Y) = W
1xm
*A
mxn
= (Y
1xL
*B
Lxm
)*A
mxn
; V
i
=
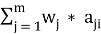
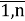
Определение потребности в видах ресурсов для производства конструктивных элементов в объёме Z 1 xm :
R
1xn
(Z) = Z
1xm
*A
mxn
; Ri =
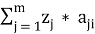
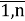
Определение потребности в ресурсах, необходимых для производства конструктивных элементов, представляющих собой остаток на конец производственного цикла:
E
1xn
= Q
K
1xm
* A
mxn
; E
i
=
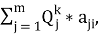
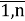
3 этап. Определение среднего количества построенной площади по типам квартир:
Д
1
xH
(Y) = Y
1
xL
* S
LxH
; Д
h
=
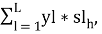
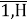
4 этап. Определение общей трудоёмкости:
Трудоёмкость изготовления ресурсов:
TT
(p)
(X) = X
1xn
*T
nx1
; TT
(p)
=
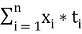
Трудоёмкость изготовления конструктивных элементов:
TT
(
K
)(
Z) = Z
1
xm
* T
K
mx
1
; TT
K
=
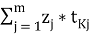
Трудоёмкость возведения зданий:
TT
(з)
(Y)
Lx
1
= B
Lxm
* T
mx
1
; TT
Bl
=
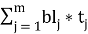
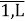
Общая трудоёмкость по строительной организации определяется:
TT
общ
= TT
(
p
)
(X) + TT
(
K
)
(Z) +
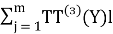
5 этап. Определение излишка ресурсов и конструктивных элементов, которые могут быть реализованы на сторону.
Определение излишка конструктивных элементов:
∆Z 1 xm (Z) = Z 1 xm — W 1 xm + Q H 1 xm — Q K 1 xm (1.10)
Определение излишка ресурсов предприятия:
∆X
1
xn
(Y,Z) = X
1
xn
+ max
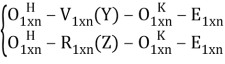
6 этап. Оптимизация эффективного размещения ресурсов строительного предприятия. Состав дохода предприятия:
— доход от реализации квартир Д 1xH * Ц (з) Hx 1 ,где Ц (з) Hx 1 — вектор цен 1м 2 общей площади квартир по типам жилых зданий, руб.;
— доход от реализации избыточных конструктивных элементов ∆Z 1 xm * Ц (К) mx 1 , где Ц (К) mx 1 — вектор цен единиц натурального объёма конструктивных элементов по видам, руб.;
— доход от реализации излишек ресурсов ∆Х 1 xn * Ц (р) nx 1 где Ц (р) nx 1 — вектор цен единиц ресурсов по видам в натуральном измерении, руб.
Первый критерий оптимальности в виде оптимизации прибыли от реализации ресурсов, конструктивных элементов и жилой площади будет иметь вид:
F
1
(X,Y,Z) = ∆X
1
xn
(Y,Z)*Ц
(
p
)
nx
1
+ ∆Z
1
xm
(Z)*Ц
(К)
mx
1
+ Д
1
xn
(Y)*Ц
(з)
Hx
1
— ∆X
1
xn
(Y,Z)*C
(
p
)
nx
1
— ∆Z
1
xm
(Z)*C
(К)
mx
1
— Д
1
xn
(Y)*C
(з)
Hx
1
→
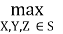
где C ( p ) nx 1 — вектор себестоимости (затрат) единиц натурального объёма ресурсов по видам, руб.; C (К) mx 1 — вектор себестоимости единиц натурального объёма конструктивных элементов по видам (без себестоимости ресурсов, необходимых для производства конструктивных элементов), руб.; C (з) Hx 1 - вектор себестоимости строительства 1 м 2 общей площади квартир по типам (без себестоимости ресурсов и конструктивных элементов, необходимых для строительства квартир) жилых зданий, руб.
Вторым критерием оптимальности примем минимизацию общей трудоёмкости производства ресурсов, конструктивных элементов и жилой площади:
F
2
(X,Y,Z) = TT
общ
→
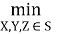
Исходя из того, что критерийпредставляет собой аддитивную функцию можно дополнительно ввести следующие частные критерии оптимальности:
F
3
(X,Y,Z) = ∆X
1
xn
*C
(
p
)
nx
1
→
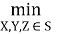
F
4
(X,Y,Z) = ∆Z
1
xm
*C
(К)
mx
1
→
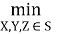
F
5
(X,Y,Z) = Д
1
xn
*C
(з)
Hx
1
→
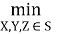
Область ограничений (S):
S
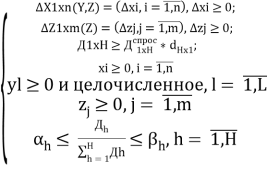
Целью задачи {3.29,3.30,3.31,3.32,3.33} является определение Х
1
xn
= (x
i
,
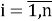
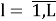
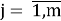
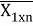
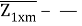
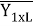
Пусть δ
К
(X,Y,Z)=
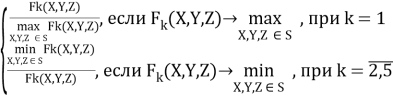
Модель определения компромиссного решения выглядит следующим образом:
F
K
(
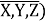
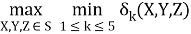
Система допущений:
1. Все нормы расхода материалов, изделий, конструкций на единицу производимой продукции известны;
2. Остатки переходящего задела на начало и на конец производственного цикла известны;
3. Трудоёмкость изготовления единицы полуфабрикатов, конструкций и др. строительных материалов, возведения конструкций известна;
4. Спрос на выпускаемую продукцию существует постоянно и определяется на основе результатов маркетинговых исследований рынка сбыта;
Таким образом, разработанная матричная модель позволяет выбрать оптимальный с точки зрения максимизации получаемой прибыли и минимизации трудоёмкости и затрат вариант производства и реализации продукции (вариант распределения имеющихся ресурсов на производство конечной и промежуточной продукции). Модель построена для строительного предприятия, которое производит и реализует:
— основную продукцию — жилые дома, здания и сооружения различных типов;
— промежуточную продукцию — строительные конструкции, которые могут быть реализованы на сторону и (или) использованы для производства конечной продукции;
— дополнительную промежуточную продукцию — сырьё, материалы и другие виды изделий, которые могут быть использованы для производства промежуточной и конечной продукции и (или) реализованы на сторону.
Литература:
1. Артеменко В. Г., Беллендир Н. В. Финансовый анализ. — М.: Издательство «ДИС», НГУЭ и У, 1997. — 128с
2. Бузырев В. В., Васильев В. Д., Зубарев А. А. Выбор инвестиционных решений и проектов: оптимизационный подход. — СПб.: Изд-во СПбГУЭФ, 1999.-224с.
3. Кондратьева Г. В. Проблемы системы финансового планирования в строительных организациях // Вестник молодежной науки. 2016.







