Актуальность данной темы доказывает тот факт, что рынок недвижимости имеет особую социальную нагрузку, удовлетворение потребностей в жилище, улучшение жилищных условий населения является важнейшим элементом социальной политики, оказывающим влияние на демографическое и социально-экономическое развитие общества. Проблема моделирования стоимости жилой недвижимости становится все более актуальной, поскольку качественный прогноз позволяет снизить риски как для органов государственного управления, так и для риелторов, оценщиков, банкиров, собственников — юридических лиц и населения.
Цель данной работы заключалась в определении минимально необходимого состава ценообразующих факторов, включение которых в регрессионную модель является обязательным в целях достижения адекватных результатов оценки, а также поиск модели, которая будет лучше всего предсказывать цену квартире на основе ее характеристик.
Задачами данного исследования являются выбор независимых переменных, характеризующих объект вторичной жилой недвижимости, изучение регрессионных моделей машинного обучения, поиск оптимальной модели, выбор переменных оказывающих наибольшее влияние на прогностическую способность моделей.
Инструментом для реализации целей и задач является Pyhon и его модули.
Исследование было проведено на основе реальных предложений на рынке вторичной жилой недвижимости города Владивосток. Наиболее полно признаки представлены на сайте [1]. Всего было собрано 1558 объявлений о продаже квартир и 35 признаков, характеризующих их, включая стоимость.
К характеристикам объектов относятся: его стоимость, площадь, количество комнат, этаж, ремонт, наличие какой-либо техники, мебели, тип санузла, наличие и вид балкона, высота потолков, является ли квартира евро квартирой, описание дома: его год постройки, район, географические координаты, микрорайон, расстояние до центра, наличие парковок и т. д.
Полученная выборка была разделена на две части: обучающую (70 %) и тестовую (30 %). Обучающая выборка использовалась для тренировки моделей, а тестовая — для определения качества их предсказания.
Чтобы оценить эффективность используемой процедуры, для каждого результата рассчитываются следующие метрики:
- Коэффициент детерминации, который отражает долю объясняемой дисперсии модели. Чем ближе значение коэффициента детерминации к 1, тем сильнее соответствие модели данным.
- Средняя абсолютная ошибка (mean absolute percentage error — МАРЕ) показывает, на сколько процентов в среднем ошибается модель.
- Медианная Абсолютная ошибка (median absolute percentage error — MedAPE) отражает серединное значение среди всех упорядоченных значений процентных ошибок.
Всего было рассмотрено 5 моделей. Первой моделью является модель линейной регрессии. Коэффициент детерминации модели равен 0.806. Это означает, что модель объясняет 80,6 % дисперсии зависимой переменной. Большинство параметров модели недостоверно отличается от нуля, но F-критерий, равный 87,99 (p-value близок к нулю) говорит, что вся модель значима. В среднем модель ошибается на 14,94 %.
Из коэффициентов линейной регрессии видно (рисунок 1), что признаки высота потолков, год постройки дома, наличие парковки, количества комнат, площадь, количество этажей дома увеличивают стоимость объекта недвижимости. Например, наличие парковки при прочих равных увеличивает стоимость квартиры на 29 393, а увеличение года постройки всего на год на 16 646. Отсутствие ремонта уменьшает стоимость квартиры при прочих равных, наибольший вклад вносит дизайнерский тип ремонта, он увеличивает стоимость на 1 835 840. Модель линейной регрессии переобучена, она сильно подстраивается под данные обучающей выборки.
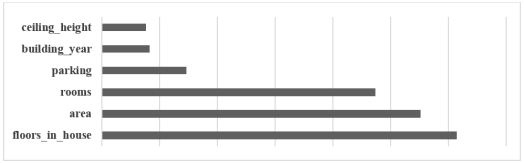
Рис. 1. Коэффициенты линейной регрессии
Коэффициент детерминации модели дерево решений равен 76 %. В среднем модель ошибается на 15,24 %. Из рисунка 2, можно сделать вывод о том, что наибольший вклад оказывает признак площади объекта, а также средняя стоимость квадратного метра по району, тип ремонта, год постройки дома, количество этажей в доме, этаж. Дерево Решений плохо справляется с объектами, площадь который более 100 м2. Какая бы площадь ни была сверх 100 м 2 модель будет предсказывать одно и то же значение, среднее значение цены по таким квартирам на обучающей выборке. Скорее всего это связано с тем, что таких квартир мало и модель не смогла корректно обучиться.
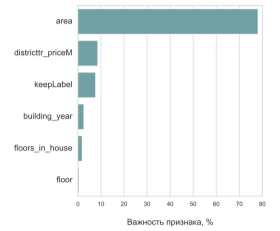
Рис. 2. Важность признаков в модели дерево решений
Коэффициент детерминации модели случайный лес равен 83,9 %. В среднем модель ошибается на 11,8 %. Из рисунка 3, можно сделать вывод о том, что наибольший вклад оказывают также признаки — площадь объекта, средняя стоимость квадратного метра по району, тип ремонта, год постройки дома, количество этажей в доме, этаж, а также количество комнат, микрорайон, район, тип балкона, стен и т. д. Модель случайный лес, гораздо лучше справляется с квартирами, площадью больше 100 м 2 , нежели модель дерево решений.
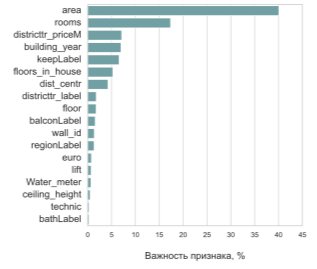
Рис. 3. Важность признаков в модели случайный лес
Коэффициент детерминации модели градиентный бустинг равен 85,5 %. В среднем модель ошибается на 12 %. Как видно из рисунка 4, наибольший вклад вносит переменная площадь, как и в предыдущих моделях. Модель лучше предсказывает значения стоимости квартир, площадь которых более 100 м кв и меньше переобучается в отличие от линейной регрессии.
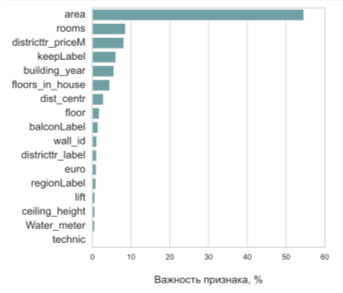
Рис. 4. Важность признаков в модели градиентный бустинг
Коэффициент детерминации модели машинного обучения CatBoost равен 86,7 %. В среднем модель ошибается на 11 %. Наибольший вклад в данную модель вносит признак, указывающий на площадь квартиры (51,2 %), наименьший — наличие телевидения (0,0013 %). Данная модель лучше всех предыдущих предсказывает значения стоимости квартир, площадь которых более 100 м кв и меньше переобучается.
В ходе данной работы были изучены модели машинного обучения и применены для предсказания цены объектов рынка жилой вторичной недвижимости города Владивосток. Всего были рассмотрены 5 моделей.
Наилучшие показатели имеет метод машинного обучения CatBoost. Он способен объяснить 86,4 % изменчивости цены независимыми переменными, которые были выбраны. В то время как модель дерево решений способна предсказывать только 76 % изменчивости цены квартиры.
На втором месте по качеству модели находить метод градиентный бустинг. Он способен объяснить 85,5 % изменчивости цены с помощью выбранных независимых переменных.
На третьем месте находится модель случайный лес с коэффициентом детерминации равным 83,9 %. На четвертом месте линейная регрессия, способная объяснить 80,6 %. Худшей обобщающей способностью обладает модель дерево решений.
Также в ходе данного исследования на основе анализа значимости независимых переменных во всех рассмотренных моделях было выявлено, что наиболее влиятельными переменными являются площадь объекта, количество комнат, средняя цена по микрорайону, тип ремонта, год постройки и его этажность, а также расстояние до центра города.
Таблица 1
Значения выбранных метрик рассмотренных моделей
|
R 2 |
MedAPE |
MAPE |
|
|
Линейная регрессия |
80,6 % |
11,61 % |
14,94 % |
|
Дерево решений |
76,0 % |
11,98 % |
15,24 % |
|
Случайный лес |
83,9 % |
8,76 % |
11,87 % |
|
Градиентный бустинг |
85,5 % |
9,68 % |
12,27 % |
|
CatBoost |
86,4 % |
8,67 % |
11,33 % |
Литература:
- Агентство недвижимости во Владивостоке Этажи. URL: https://vl.etagi.com/ (Дата обращения: 19.06.2022).







