В данной статье изучаются отображения алгебр квадратичных матриц четвертого порядка над алгебрах фон Неймана типа I, заданные с помощью отображения сохраняющей коммутативности, и определяется общий вид.
Ключевые слова: отображение, алгебра фон Неймана, коммутативность, матрица.
В теории операторов отображения играют важную роль при изучении алгебр операторов. Отображения, такие как изоморфизм, гомоморфизм, дифференцирование и автоморфизм различных алгебр операторов, определённых в гильбертовых пространствах, изучались в ряде исследований ([1]-[5]). Отображения сохраняющие коммутативность на различных алгебрах операторов изучались многими учеными ([2]-[4]), в которых одно из отображений в операторных алгебрах. В большинстве случаев было показано, что если отображение сохраняет коммутативность, тогда это отображение будет представлено изоморфизмом Йордана и аддитивным отображением.
Мы рассмотрим отображение алгебр квадратных матриц над алгебрах фон Неймана типа I, заданное с помощью отображения сохраняющей коммутативности.
Определение 1.
Если для отображения
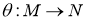
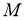
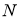
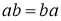
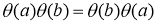
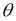
Определение 2.
Если для отображения
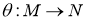
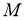
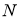
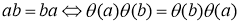
Пусть
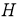
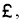
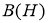
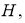
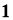
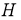
Определение 3.
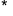
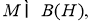
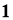
Пусть
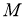
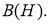
Коммутантом множества
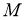
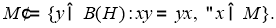
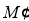
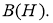
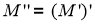
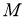
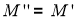
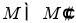
Если

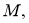
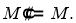
Так как
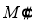
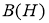
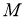
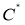
Норму элемента (оператора)
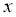
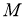
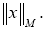
Простейшими примерами алгебр фон Неймана являются алгебра
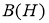
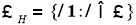
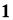
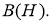
Множество
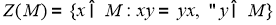
называется
центром
алгебры фон Неймана
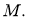
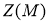
Если
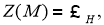
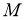
Обозначим через
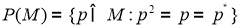
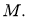
Если для проекторов
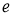
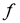
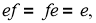
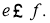
Проекторы
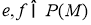
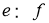
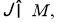
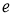
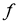
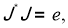
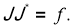
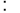
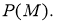
Проектор
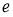
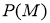
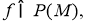
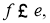

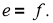
Алгебра фон Неймана
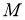
—конечной
, если
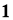
—
полуконечной
, если каждый ненулевой проектор из
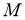
—
бесконечной
, если
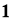
—
собственно бесконечной
, если каждый ненулевой центральный проектор из
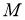
—
чисто бесконечной или типа
III, если каждый ненулевой проектор из
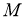
Алгебра фон Неймана
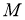
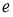
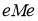
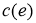
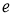
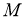
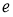
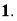
Алгебра фон Неймана
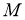
Произвольная алгебра фон Неймана
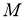
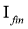
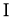
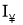
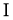
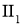
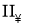
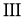
В работе [4] изучались отображения сохраняющие коммутативность на алгебрах фон Неймана не имеющие центральных слагаемых типа
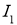
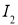
Теорема 1. ([4]).
Пусть алгебры
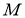
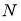
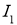
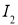
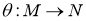
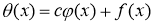
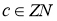
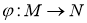
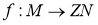
Пусть отображение
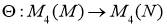
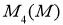
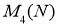
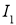
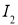
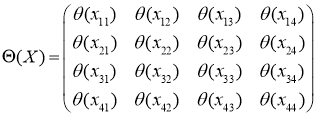
где
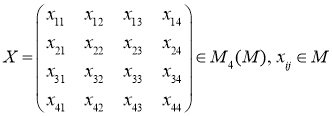
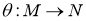
Теорема 2.
Пусть отображение
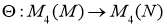
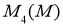
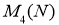
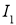
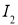
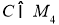
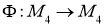
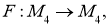
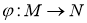
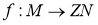

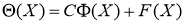
где элемент
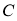
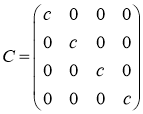
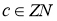
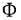
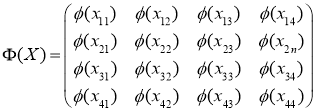
а отображение
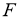
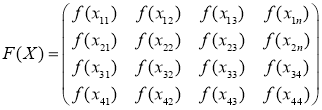
Литература:
- Муратов М. А., Чилин В. И. Алгебры измеримых и локально измеримых операторов. — Працi Iн-ту математики НАН Украïни, 2007. — 390 с.
- Molnár L, Šemrl P. Non-linear commutativity preserving maps on self-adjont operators. Q. J. Math. 2005;56:589–595.
- Brešar M, Šemrl P. Commutativity preserving linear maps on central simple algebras. J.Algebra. 2005;284:102–110.
- M. Brešar, C. R. Miers, Commutativity preserving mappings of von Neumann algebras, Canad. J. Math. 45 (1993) 695–708.
- Аюпов Ш. А., Кудайбергенов К. К., Каландаров Т. С., *-автоморфизмы алгебры Аренса ассоциированной с алгеброй фон Неймана типа I. // Узб. Мат. Жур. — Ташкент, 2007. — № 4. — C. 9–17.







