При проектирования новых и оценке несущей способности существующих лестниц из сборного и монолитного железобетона, лестничные марши рассчитываются в «ручном» расчете как шарнирно опертые однопролетные балки, в расчете с использованием ПК — как участки плоских плит, сочлененных с лестничными площадками. При этом за расчетную высоту сечения марша принимается высота по наиболее узкому месту между ступенями, а сами ступени учитываются дополнительной нагрузкой к собственному весу марша. При оценке прочности и трещиностойкости конструкций марша, расчет по наиболее слабому участку элемента является очевидным. Однако, при расчете деформаций марша (проверка прогибов и «зыбкости»), исключение из работы ступеней уменьшает изгибную жесткость марша, так как не рассматривается пилообразное изменение его высоты сечения по длине. Целью данного исследования является определение влияния ступеней на изгибную жесткость железобетонных маршей, и целесообразность их учета в расчетах.
Ключевые слова: железобетонный марш, определение прогибов.
Описание объекта исследования
Объектом исследования выбран лестничный марш с размерами ступеней: высота подступенка 150мм, ширина проступи 300мм (высота ступени относительно плитной части марша — 135мм). Длину марша принимаем равной 6.3м (для удобства последующего варьирования высоты сечения). Материал — бетон В25, с начальным модулем упругости 30000МПа и коэффициентом Пуассона v=0.2. С целью исключения влияния податливости переходных площадок и продольной силы в марше, его расчетная схема принимается в виде горизонтальной однопролетной шарнирно опертой балки. Для расчета вырезаем участок шириной 100мм.
Оценку влияния ступеней на жесткость марша, рассматриваем его работу при различных соотношениях толщины плитной части марша к высоте ступеней: 1:1, 1.5:1; 2:1; 3:1; 4:1; 5:1; 6:1; 10:1 (толщина плитной части от 135мм до 1350мм).
В ходе расчетов, рассматриваем три варианта загружений: равномерно распределенная нагрузка 500кг/м, сосредоточенная нагрузка 250кг в середине или четверти пролета.
Описание численной модели
Расчет ведется в ПК Лира-САПР 2017. Плитная часть марша моделируется четырехугольными элементами КЭ21, ступени — четырехугольными КЭ21 и треугольными КЭ22. Толщина всех элементов 100мм. Плитная часть марша по высоте состоит из четырех КЭ21. На половине высоты плитной части (по нейтральной оси) с левого и правого конца балки наложены связи — по X и Z, и по Z соответственно. Ступени по высоте состоят из одного КЭ21 или КЭ22 (в зависимости от положения по длине балки). Нагрузки прикладываются к узлам верхней грани плитной части, распределенная нагрузка так же задается в виде последовательности сосредоточенных сил.
В ходе расчета, для каждого варианта загружения и отношения толщины плитной части к высоте ступеней, сравниваем работу маршей без учета и с учетом наличия ступеней в КЭ схемах (рис. 1 и рис. 2).

Рис. 1. КЭ схема марша с плитной частью толщиной 270мм без учета наличия ступеней

Рис. 2. КЭ схема марша с плитной частью толщиной 270мм с учетом наличия ступеней
Результаты расчетов КЭ схем сведены на графики, представленные на рис. 3 ÷ рис. 5.
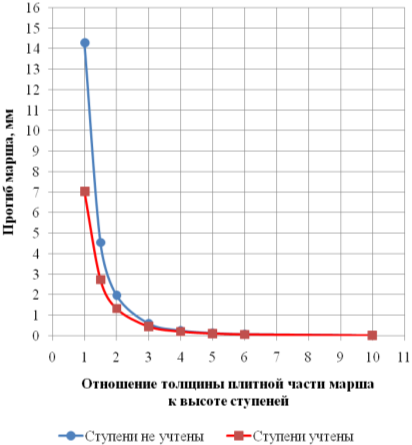
Рис. 3. Прогибы марша под действием равномерно распределенной нагрузки
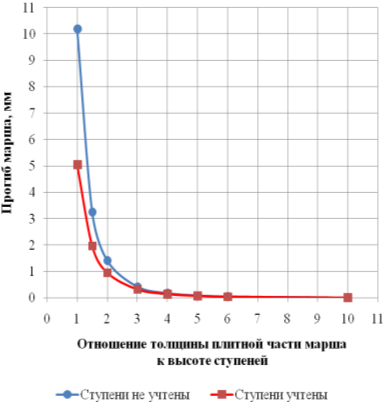
Рис. 4. Прогибы марша под действием сосредоточенной нагрузки в середине пролета
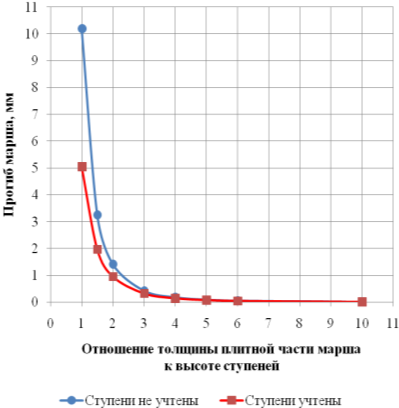
Рис. 5. Прогибы марша под действием сосредоточенной нагрузки в четверти пролета
Как следует из расчета, для всех рассмотренных вариантов приложения нагрузок, учет ступеней в расчетной схеме марша позволяет уменьшить его прогиб. Так, при толщине плитной части марша равной 200мм, наблюдается двухкратное уменьшение прогиба. Наибольшее влияние учета ступеней в расчете марша наблюдается при соотношении толщины плитной части марша к высоте ступеней в диапазоне от 1:1 до 3:1, при большем соотношении влияние ступеней на изгибную жесткость марша уменьшается.
Для дальнейшего анализа, рассмотрим зависимость между прогибом, вычесленным с учетом ступеней (f уч. ст. ) и без учета ступеней (f без уч. ст. ) в виде зависимости:
f уч. ст. = K ∙ f без уч. ст.
График зависимости коэффициента K от отношения толщины плитной части марша к высоте ступени, для трех рассмотренных вариантов загружения марша, приведен на рис. 6.
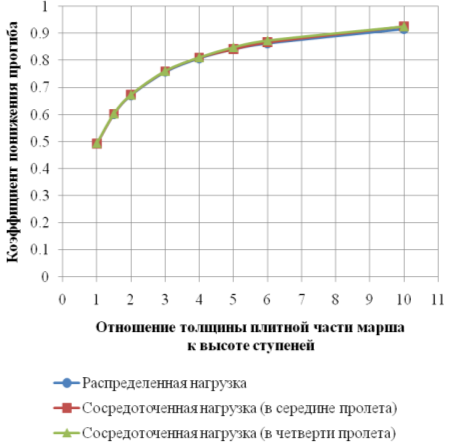
Рис. 6. Зависимость коэффициента K от отношения плитной части марша к высоте ступени
Как видно из графика, вид нагрузок не влияет на величину коэффициента K (все 3 графика сливаются в один).
Таким образом, на основе геометрии марша, возможна оценка целесообразности учета ступеней марша при определении его изгибной жесткости. Например, при наличии «запаса» по прогибам при расчете «плоского» марша, в учете влияния ступеней необходимость отсутствует. В случае превышения прогибов над предельно допустимыми, появляется возможность оценить целесообразность создания отдельной схемы для учета влияния ступеней на жесткость марша и уменьшение прогибов.
Выводы
- Получена КЭ модель железобетонного марша, позволяющая учесть ступени в изгибной жесткости марша при расчетах по деформациям.
- Наиболее выгодным является учет ступеней в расчетах по деформациям при соотношении толщины плиты марша к высоте ступени от 1:1 до 3:1.
- Получена графическая зависимость для оценки целесообразности создания отдельной схемы для учета влияния ступеней на жесткость марша для уменьшения прогибов
Литература:
1. Бондаренко, В. М. Примеры расчета железобетонных и каменных конструкций: учебное пособие для студентов высших учебных заведений, обучающихся по специальности «Промышленное и гражданское строительство» направления подготовки дипломированных специалистов «Строительство» / В. М. Бондаренко, В. И. Римшин; В. М. Бондаренко, В. И. Римшин. — Москва: Высш. шк., 2006. — (Для высших учебных заведений. Строительство). — ISBN 5–06–004437–8. — EDN QNMLGV.
2. Малахова, А. Н. Проектирование железобетонных и металлических лестниц / А. Н. Малахова, Д. В. Морозова; А. Н. Малахова, Д. В. Морозова. — Москва: Изд-во Ассоц. строит. вузов, 2011. — 167 с. — ISBN 978–5–93093–550–9. — EDN QNPEPV.
3. Абрашитов, В. С. Анализ несущей способности лестничного марша при нагрузках, не предусмотренных проектом / В. С. Абрашитов, А. Н. Жуков, Е. В. Савинова. — Текст: непосредственный // Молодой ученый. — 2014. — № 20 (79). — С. 97–101. — URL: https://moluch.ru/archive/79/13989/ (дата обращения: 21.07.2022).
4. Мишуренко, Н. А. Обследование монолитной лестничной клетки / Н. А. Мишуренко, А. Н. Сорокин, А. В. Домацкий // Модернизация научной инфраструктуры и цифровизация образования: Материалы XI Международной научно-практической конференции. В 2-х частях, Ростов-на-Дону, 23 июня 2021 года. — Ростов-на-Дону: ООО «Издательство ВВМ», 2021. — С. 26–29. — EDN JZMOCV.
5. Терентьев, А. А. Методика комплексного обследования и оценки технического состояния лестничных маршей / А. А. Терентьев // ScienceRise. — 2015. — Т. 8. — № 2(13). — С. 41–46. — DOI 10.15587/2313–8416.2015.48207. — EDN UDLFDR.
6. Шувалов, Н. А. Исследование и оценка технического состояния конструкции лестничного марша монолитно-каркасного жилого дома / Н. А. Шувалов, В. С. Малютин // Национальная Ассоциация Ученых. — 2015. — № 2–4(7). — С. 50–53. — EDN WBIUIH.







