В соответствии с приказом Министерства образования и науки РФ «Об утверждении Федерального государственного образовательного стандарта основного общего образования» от 17 декабря 2010 года № 1897, зарегистрированного Минюстом России 1 февраля 2011 года, Уставом МАОУ СОШ № 25 г. Томска, Федеральными государственными образовательными стандартами общего образования, методическими рекомендациями вышестоящих организаций по их внедрению было разработано, утвержденоивведено в действие приказом № 61 от 23 марта 2012 года Директора МАОУ СОШ № 25 Т. И. Петрачковой, утверждено на педагогическом совете и согласовано с профсоюзной организацией «Положение о внедрении в образовательный процесс стандартов второго поколения (ФГОС ООО)». [3] Данное Положение предусматривает порядок внедрения в Школе ФГОС. Переход к внедрению стандартов второго поколения осуществляется в пилотном режиме. Согласно дорожной карте по внедрению ФГОС ООО [2] при разработке предметных рабочих образовательных программ каждый педагог школы должен разработать систему оценки планируемых результатов освоения программы. Система оценивания результатов обучения по математике представляет целостную систему, в которой сочетаются различные практики, методики, технологии и инструментарии.
Каждый педагог должен оценивать успешность освоения программного материала учащимися. Для эффективной оценки знаний учащихся существуют некоторые виды контроля (Рис.1), которые регламентированы локальным актом — «Положением о системе оценок, форм, порядке и периодичности текущего контроля, промежуточной аттестации обучающихся и государственной (итоговой) аттестации».
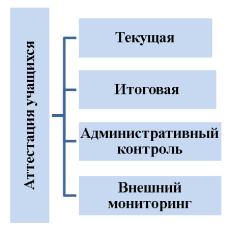
Рис.1. Виды аттестации учащихся
Объектом текущей аттестации учащихся являются планируемые результаты изучения учебного материала [1, с.29]. Для тематического контроля я разработала и успешно применяю маршрутные листы. В начале четверти каждый учащийся получает маршрутный лист, в котором указываются тема и формы контроля (Рис.2).
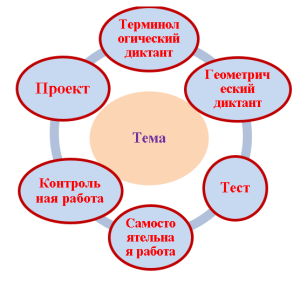
Рис.2. Формы тематического контроля
Такой лист является ориентиром учащегося: каждый знает, что необходимо сдать, в какой форме и более сильные учащиеся обычно частично проходят некоторые формы контроля раньше, чем остальные учащиеся. А во время урока или внеурочных занятий, или консультаций эти учащиеся уже могут быть консультантами и помощниками для учителя. Можно сказать, что формы контроля уже известные, но изменились дети, изменились и учителя. Уже не получится обучать детей, не применяя современных методов обучения. Нельзя говорить, что все должно измениться и методы тоже должны быть новыми. Необходимо применять некоторые известные уже методы, только по-новому. О каждой форме контроля расскажу подробно.
Терминологические диктанты позволяют учащимся ясно, точно и грамотно излагать свои мысли в устной и письменной форме. Знание терминов, точных определений и свойств геометрических фигур позволит в дальнейшем совершенствовать навыки их применения как опоры при решении задач. Терминологические диктанты могут проводиться как в устной, так и в письменной форме. Может быть использована парная или групповая форма работы. Например, учащиеся могут рассказывать определения и формулировки свойств, или теорем друг другу и оценивать ответы. Интересная форма терминологического диктанта — решение анаграмм. Например, можно предложить решить следующие анаграммы: РТОЕОЗК (ОТРЕЗОК), ЯПЯРАМ (ПРЯМАЯ), ЛУГО (УГОЛ), ЧЛУ (ЛУЧ), ОКАЧТ (ТОЧКА). После их решения необходимо дать определение каждой геометрической фигуре и рассказать друг другу. После этого учитель может задать вопросы: «Всем ли фигурам вы сможете дать определение? Почему?». Такая работа способствует развитию логического мышления, а взаимопроверка позволяет учащимся вырабатывать более ответственное отношение к оценке деятельности, как одноклассников, так и своей. Интересно можно построить работу по проверке теоретического материала в малых группах, которая позволяет решать не только познавательные задачи, но и способствует воспитанию толерантности и уважения мнения других.
Проведение геометрических диктантов, особенно на начальной стадии изучения геометрии, необходимо, так как решение каждой геометрической задачи начинается с рисунка, составленного по условию задачи и анализа данных. При этом учащиеся, используя различные языки математики (словесный, символический, графический), должны свободно переходить с одного языка на другой. Учащиеся должны уметь по рисунку сделать символическую запись (описать геометрические фигуры и их взаимное расположение), и наоборот — по символической записи создать геометрическую интерпретацию. И снова работа в парах поможет провести этот этап урока наиболее интересно.Такая работа с учащимися по развитию навыков изображения планиметрических фигур и простейших геометрических конфигураций позволяет совершенствовать навыки применения свойств геометрических фигур как опоры при решении задач.
Такая форма контроля как тест позволяет оперативно провести контроль знаний учащихся. Тесты не должны содержать много заданий и по форме ответов должны быть разнообразными. Так можно предложить тест из пяти вопросов, причем первые три задания с выбором ответа, одно задание не имеет ответа (его учащиеся должны получить самостоятельно), и последнее задание на соотнесение предложенных вариантов ответа с изображениями на рисунках. После того, как учащиеся ответят на вопросы тестовых заданий, они могут провести взаимопроверку с выставлением оценок друг другу. После этого необходимо провести анализ полученных ответов и результатов оценок. Деятельность учащихся по взаимооценке позволяет решать такую задачу в направлении личностного развития ребенка как способность принимать самостоятельные решения. Тесты могут проводиться как в письменной форме, так и с помощью компьютеров. Интерактивные тесты, составленные учителем или самими учащимися, позволяют развивать познавательные УУД и формируют метапредметные способы познания программного материала.
При решении задач учащиеся имеют возможность закрепить полученные знания, искать пути и способы решения. Такую работу можно проводить в группах по 7–8 человек. Причем, до начала самостоятельной работы я формирую группу по принципу: в каждой группе должны быть учащиеся с различным уровнем подготовки. Сначала условие задачи, возможный ход ее решения обсуждается в группе. Затем каждый учащийся оформляет письменное решение самостоятельно. Таким образом, создаются условия для успеха каждого ученика. Такая форма проведения самостоятельной работы позволяет развивать навыки коммуникативного общения и диалоговой деятельности учащихся.
Контрольная работа может быть представлена в традиционной форме: определенное количество заданий по тематике образовательного курса, но можно предложить рейтинговую контрольную работу. Каждая задача имеет «вес», определяемый баллами. Далее необходимо учащимся предложить шкалу оценки: за какое количество баллов какая оценка будет выставлена. И тогда у каждого ребенка есть выбор: можно решить несколько заданий, которые оценены небольшим количеством баллов или решить меньшее количество, но более сложных задач.
И наконец, итог большого тематического раздела я заканчиваю защитой проектов. Это могут быть информационные проекты, в которых учащиеся собирают информацию по данной теме, выходящую за рамки учебника, исторические сведения, информация об ученых, которые внесли вклад в развитие данного раздела. Очень ценю практико-ориентированные проекты, когда в качестве продукта проекта учащиеся представляют учебно-методические материалы для уроков (кроссворды, подбор задач, мультимедийные приложения). Проектная деятельность позволяет развивать в направлении личностного развития учащихся интерес к математическому творчеству и математических способностей.
Для эффективного достижения цели урока — обобщения и систематизации знаний — оценка деятельности учащихся на каждом этапе урока необходима. Наибольшего эффекта оценки знаний учащихся на современном уроке можно достигнуть методом самооценки и взаимооценки. Для этого на уроке могут предложены критерии оценивания: 2 балла — задание выполнено полностью верно (или ответ на вопрос верный с объяснением), 1 балл — ответ неполный (или ответ получен, но отсутствует объяснение), 0 баллов — ответ неверный или отсутствует. В течение урока учащиеся оценивают свою деятельность на каждом этапе. В конце урока баллы суммируются, и каждый учащийся выставляет себе оценку за урок. Таким образом, на уроке присутствует критериальный подход к оценке деятельности учащихся.
Работа в творческих группах при реализации проектов школы «Самоорганизация коллектива школы по развитию креативного мышления» и «Внедрение в образовательный процесс стандартов второго поколения (ФГОС ООО) предполагает не ограничиваться по данной теме только в рамках школы. Это и обобщение педагогического опыта, и выступление с докладами на семинарах и конференциях, различные публикации. Также инновационные методические разработки успешно были представлены на различных конкурсах и фестивалях различного уровня.
Учитывая все особенности применения современных форм и методов оценивания достижений учащихсяможно сделать выводы:
— в направлении личностного развития применение форм самооценки и самоконтроля учащихся способствует развитию качеств мышления, необходимых для адаптации в современном обществе;
— в метапредметном направлении современные методы оценивания позволяют формировать общие способы интеллектуальной деятельности, характерные для математики и являющиеся основой познавательной культуры;
— в предметном направлении способствует овладению математических знаний и умений, необходимых для продолжения образования;
— сочетание различных форм и методов оценивания стимулирует познавательную активность и способствует высокой степени мотивации учащихся.
Литература:
1. Боженкова Л. И. Критериальное оценивание достижений учащихся 7–9 классов в обучении геометрии: Научно-методическое пособие//Л. И. Боженкова, Е. В. Соколова. — ФГБОУ ВО МГПУ, Изд-во: Эйдос, 2016
2. Дорожная карта по введению федерального государственного образовательного стандарта основного общего образования (ФГОС ООО) МАОУ СОШ № 25 г.Томска. URL: http://school25.tomsk.ru/index.php/fgos
3. Положение о внедрении в образовательный процесс стандартов второго поколения (ФГОС ООО). URL: http://school25.tomsk.ru/index.php/fgos
4. Цибульская Е. В. Технология самооценки и самоконтроля собственной деятельности как способ активизации обучения на уроках математики // Молодой ученый (спецвыпуск). Казань. ООО «Молодой ученый», № 2.1, 2015. С.32–33







