Основным способом обеспечения динамической комфортности пребывания людей на зрительских трибунах является ограничение низшей частоты собственных колебаний конструкций трибун [1÷4]. В случае железобетонных конструкций, расчет на динамическую комфортность, как правило, выполняется после подбора сечения и армирования конструкций по «стандартному» расчету по I и II группам предельных состояний. При этом, для конструкций непосредственно трибун, как правило (в виду относительно небольших пролетов и развитого поперечного сечения), низшие частоты собственных колебаний находятся в пределах, либо чуть ниже допустимых значений. В случае подтрибунных балок (в литературе так же встречается наименование балки-гребенки, шпангоуты) сечения, полученные по «стандартному» расчету, являются недостаточными по критерию частот собственных колебаний.
Данная статья посвящена исследованию собственных колебаний однопролетных подтрибунных балок.
Ключевые слова: трибуны, подтрибунные балки, балки-гребенки, шпангоуты, модальный анализ, собственные колебания, динамическая комфортность, оптимальное проектирование, стадион.
Обоснование актуальности темы
Фактором, усложняющим анализ частот собственных колебаний подтрибунных балок, является то, что при расчете «общей» схемы сооружения, определяются частоты собственных колебаний для всех заданных элементов, что делает их анализ практически невозможным [4].
С целью упрощения и ускорения расчета подтрибунных балок, для них создаются отдельные расчетные схемы. Как правило, подтрибунные балки моделируются стержневыми КЭ (см. рис. 1).
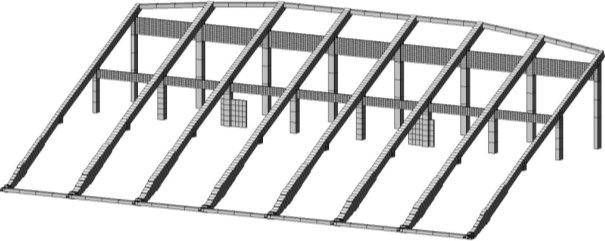
Рис. 1. КЭ-моделирование балок-гребенок стержневыми элементами
Подобная схема не учитывает влияние ступеней на жесткость балок, таким образом, величины собственных колебаний являются заниженными. Для учета ступеней, более корректной является схема с заданием подтрибунных балок пластинчатыми элементами (см. рис. 2).
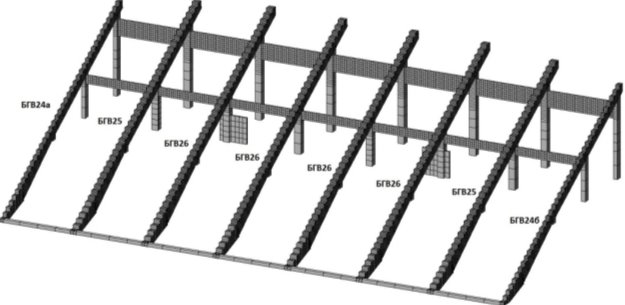
Рис. 2. КЭ-моделирование балок-гребенок пластинчатыми элементами
В практике проектирования подтрибунных балок, повышение частот собственных колебаний, как правило, достигают за счет увеличения высоты поперечного сечения балок. Данный расчет, даже при использовании ПК, выполняется итерационно, и состоит из последовательной проверки частот собственных колебаний подтрибунных балок с пошаговым увеличением высоты сечения (например, на 10–15 % от текущей высоты сечения) для достижения требуемых частот.
Даже в пределах одного типоразмера подтрибунной балки данный подход является: во-первых, трудоемким, во-вторых — не обеспечивает оптимального расхода материалов (как и любой «пошаговый» способ подбора параметров).
Таким образом, уменьшение итераций при расчете, и, в целом, развитие методологии проектирования подтрибунных балок, является актуальной темой.
Постановка задачи
В первом приближении, исследуем колебания однопролетной подтрибунной балки.
Рассмотрим известное выражение для определения частот собственных колебаний однопролетной шарнирно опертой балки:
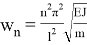
где n — номер частоты;
l — пролет балки;
E — модуль упругости материала балки;
J — момент инерции поперечного сечения балки;
m — погонная масса балки.
Как следует из выражения (1), вариация размеров ступеней подтрибунной балки (за счет изменения изгибной жесткости и погонной массы балки в целом) так же приводит изменению частот собственных колебаний по некоторой степенной зависимости.
Задачей данной работы является выявление и качественный анализ данной зависимости в ходе численного исследования.
Описание объекта исследования
Объектом исследования выбрана однопролетная железобетонная подтрибунная балка. Так как параметры ступеней балки задаются расположением на них трибун, и в общем случае имеют индивидуальные размеры и расположение на подтрибунной балке, для исследования принимаем одинаковые размеры ступеней по всей длине балки.
Оценку влияния размеров ступеней на частоты собственных колебаний выполняем путем модального анализа расчетных схем подтрибунных балок в ПК Лира-САПР 2017 при постоянных размерах ступеней, и различных пролетах и высотах подтрибунных балок, аналогично с изучением влияния ступеней на изгибную жесткость лестничных маршей в работе [5]. Ступени балок (для удобства варьирования прочих параметров балок, производим «уменьшение масштаба» ступеней) имеют следующие размеры: высота «подступенка» 150мм, ширина «проступи» 300мм (высота ступени относительно плоской части балки — 135мм). Ширина балки — 100мм.
Модальный анализ проводим при варьировании следующих параметров:
– соотношение толщины плоской части балок к высоте ступеней: 1:1, 1.5:1; 2:1; 3:1; 4:1; 5:1; 6:1; 8:1; 10:1 (толщина плоской части от 135мм до 1350мм);
– соотношение пролета балки к ширине «проступи» 7:1, 10:1; 15:1; 20:1; 27:1 (пролет балки от 2025мм до 8505мм);
– учет наличия ступеней в расчетной схеме заданием их в КЭ модели, либо только отдельной нагрузкой по верху балок.
Материал — бетон В25, с начальным модулем упругости 30000МПа и коэффициентом Пуассона v=0.2. Расчетная схема принимается в виде горизонтальной однопролетной шарнирно опертой балки.
Описание численной модели
Построение КЭ схемы аналогично принятой в [5], пример рассматриваемых КЭ моделей — рис. 3, рис. 4.

Рис. 3. КЭ схема подтрибунной балки пролетом 8,505м с плоской частью толщиной 810мм (схема без учета ступеней, их вес задан отдельной нагрузкой)

Рис. 4. КЭ схема подтрибунной балки пролетом 8,505м с плоской частью толщиной 810мм (схема с учетом ступеней)
Для дальнейшего анализа, вводим безразмерный коэффициент K w , показывающий отношение собственной частоты балки, полученной с учетом ступеней (w уч.ст ), к частоте (w без уч.ст . ), полученной без учета ступеней (учет ступеней нагрузками):
K w = w уч.ст / w без уч.ст . (2)
График зависимости коэффициента K w для различных толщин плоской части балок и величин пролетов балок приведен на рис. 5 и рис. 6.
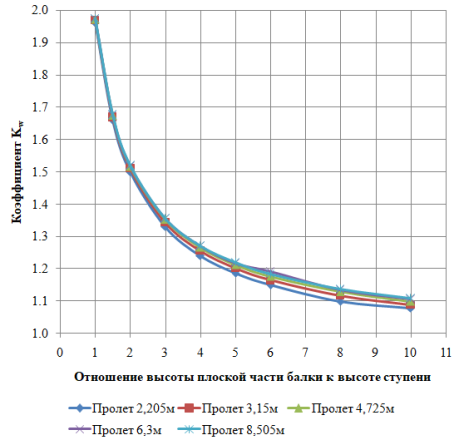
Рис. 5. Зависимость коэффициента K w от отношения высоты плоской части балки к высоте ступени
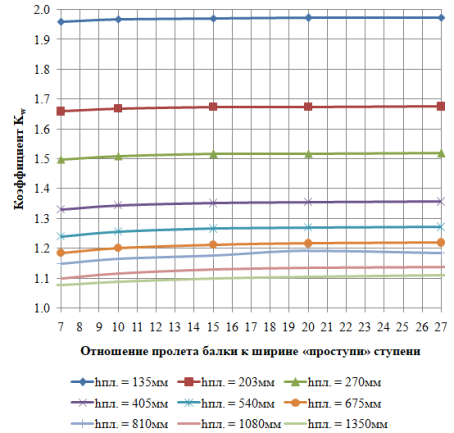
Рис. 6. Зависимость коэффициента K w от отношения пролета балки к ширине «проступи» ступени
Как и ожидалось, учет ступеней при модальном анализе привел к повышению низших частот собственных колебаний балок.
При этом, первоначальное предположение о влиянии размеров ступеней на частоты колебаний нашло лишь частичное подтверждение: изменение высоты ступени (рис. 5 ) действительно задает некоторую степенную функцию изменения частоты колебаний, а изменение ширины «проступи» ступени относительно пролета балки (рис. 6 ) почти не оказывает никакого влияния на частоту собственных колебаний.
Выводы
- Произведен модальный анализ 40 расчетных схем однопролетных подтрибунных балок для различных высот плоской части и пролетов при постоянных размерах ступеней.
- Подтверждено, что учет ступеней в расчетных схемах балок позволяет получить более высокие частоты собственных колебаний балок (в рассмотренных схемах повышение составило от 10 до 90 %) по сравнению с расчетом без их учета.
- Влияние ширины «проступи» ступеней (при одинаковом размере «проступи») на частоты колебаний при однопролетной схеме работы балок не выявлено.
- Учет ступеней в работе подтрибунных балок в ходе модального анализа является обязательным условием оптимального проектирования.
Литература:
1. Назаров, Ю. П. Анализ и ограничение колебаний конструкций при воздействии людей / Ю. П. Назаров, В. Н. Симбиркин // Вестник ЦНИИСК им. В. А. Кучеренко «Исследования по теории сооружений». — 2009. — № 1. — С. 10–18. — EDN MSMCNR.
2. Сафронов, В. С. Анализ современного состояния развития теории динамического воздействия от танцующих групп людей на строительные конструкции зданий и сооружений / В. С. Сафронов, А. В. Антипов // Строительная механика и конструкции. — 2014. — № 1(8). — С. 5–15. — EDN SYRZQJ.
3. Сафронов, В. С. Колебания и прочность современных несущих конструкций зданий при проведении массовых развлекательных мероприятий / В. С. Сафронов, А. В. Антипов // Строительная механика и конструкции. — 2013. — № 2(7). — С. 44–55. — EDN RTJWDT.
4. Максутов, Т. Р. Опыт проектирования каркаса БСА «Лужники»/ Т. Р. Максутов // АО «Казанский Гипронииавиапром» «Новое в архитектуре, проектировании строительных конструкций и реконструкции: материалы научно-практической конференции 2016, в честь 75-летия предприятия». — 2016 — С. 85–95.
5. Трофимов, Д. П. Влияние ступеней на изгибную жесткость железобетонных лестничных маршей / Д. П. Трофимов. — Текст: непосредственный // Молодой ученый. — 2022. — № 29 (424). — URL: https://moluch.ru/archive/424/94106/ (дата обращения: 01.08.2022).







