Большинство систем в природе сочетают два свойства: во–первых, они очень велики, часто многогранны, многообразны и сложны, а во–вторых они формируются под действием очень небольшого количества простых закономерностей, и далее развиваются, подчиняясь этим правилам. Это самые разные системы, начиная от кристаллов, заканчивая экосистемами и биологическими объектами (от листа папоротника до человеческого мозга). Фракталы являются как раз такими объектами: с одной стороны — сложные (содержащие бесконечно много элементов), с другой стороны — построенные по очень простым законам. Благодаря этому свойству, фракталы обнаруживают много общего со многими природными объектами. Одной из разновидностью фракталов является L-система.
L-система или система Линденмайера — это параллельная система переписывания и вид формальной грамматики, для которой необходим графический метод отображения. L-система выгодно отличается от природного объекта тем, что он имеет строгое математическое определение и поддаётся строгому описанию и анализу. Применение фракталов является одним из эффективных решений ряда задач во многих сферах жизнедеятельности человека. Для эффективного моделирования дерева при помощи L–системы является язык программирования Python.
Перейдя к проектированиюпараметрической L–системы создается новый проект в Blender и устанавливается плагин lsystem (рис 1).
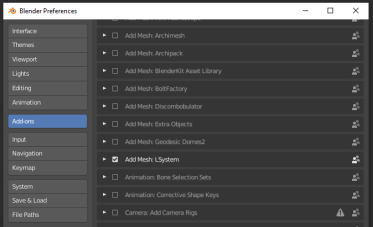
Рис. 1. Установка плагина
Подключается библиотека lsystem.exec. Подготовка завершена, приступим к разработке L–системы. Определим первичный вид сегмента, который будет являться правилом для аксиомы. Для этого рассмотрим расположение ветвей реального дерева на рисунке 2.


Рис. 2. Расположение ветвей дерева
На нем прослеживаются повторяющиеся структуры, которые можно разделить на сегменты. Красным цветом выделено первое поколение системы, оранжевым — второе. Создадим алгоритм, который схематично (без учета вариаций) отобразит одину итерацию. Для этого создадим переменную exec в которую поместим обращение к lsystem.exec.Exec(). Теперь зададим функцие exec.set_axiom() аргумент «X» как аксиому, а в качестве правила возьмем «X =F [+F]–F». Завершающим шагом будет добавление параметров min_iterations и angle, отвечающих за количество поколений и за угол наклона соответсвенно. Получившийся код показан на рисунке 3.
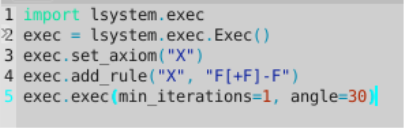
Рис. 3. Алгоритм для первого поколения
Запустим получившийся скрипт и проанализируем получившуюся модель, которая представлена на рисунке 4.
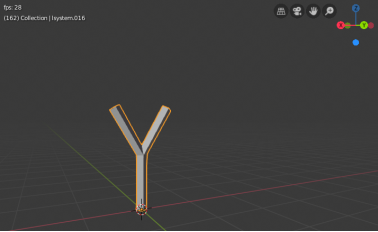
Рис. 4. Модель первого поколения
Можем заметить, что созданное правило подходит для реализации поставленной задачи. Скорректируем угол наклона ветвей, изменив его на 45°, и дополним правило так, чтобы из каждого конца ветви появлялся аналогичный сегмент. Так же, добавим дополнительный шаг в начале, чтобы увеличить длину ствола дерева.Получившиеся правило «X=FF [+FX] [–FX]» позволит отобразить второе и даже более высокое поколение, что можно увидеть на рисунке 5.
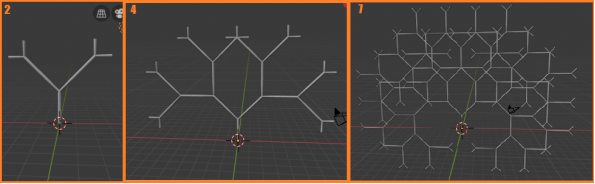
Рис. 5. Модели высокого поколения
Модель генерируется корректно, перейдем к добавлению поворота по оси Y и приданию правдоподобности. Для этого добавим:
– символ «/» позволяет совершить вращение ветви;
– символ «!» уменьшает диаметр ветки каждую итерацию;
– символ «¤» задает для аксиомы первоначальный радиус.
Получилось правило «X =!FF [+/FX] [–/FX]» и аксиома «¤(1)X» Рассмотрим изменения для шести поколений на 3Dмодели, представленной на рисунке 6.
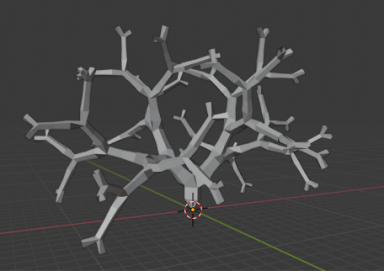
Рис. 6. Модель с трехмерной генерацией ветвей
Структура уже больше похожа на взятое за основу дерево, добавим сглаживание модели.Дляэто в аксиоме изменим аргумент на «p(subsurf)¤(1.5)X», что задаст тип пера. Также скорректируем радиус сегментов и добавим поверхность. Получившийся результат представлен на рисунке 7.

Рис. 7. L-система со сглаживанием поверхности
Такой вариант больше подходит для зимних ландшафтов. Теперь создадим правило, отрисовывающее полигональный лист.Для этого есть специальный тип генерации «surface», позволяющий делать плоскости с заданными гранями. В итоге получилась функция с такими условиями: «exec.add_rule(«L«, " [^^:p(surface)– F+F+F– +(180)– F+F+F;]")».
Для большей эффектности добавим нашему дереву третье ответвление, для того, чтобы крона была более густая. Получившая модель показана на рисунке 8.
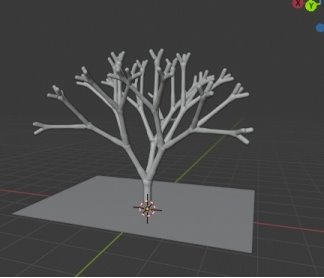
Рис. 8. Модель дерева
Теперь отредактируем остальные правила так, чтобы удобно было генерировать листья. Для этого разобьем повороты на множество маленьких действий. Так листа будет иметь менее упорядоченный вид.Затем разобьем большое правило на несколько переменных. Получившийся код показан на рисунке 9.
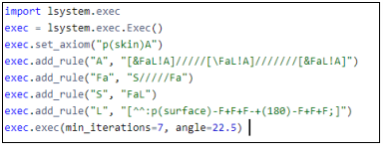
Рис. 9. Алгоритм для дерева с листьями
На рисунке 10 представлена модель дерева, созданного по алгоритму.
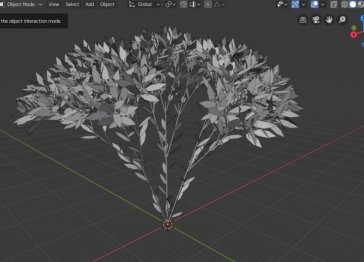
Рис. 10. Дерево с листьями
Из результатов разработки, можно сделать вывод, что данные модели подходят для использования в архитектурных проектах и компьютерных играх. Данный скрипт в совокупности с получившейся L–системой, способен сгенерировать множество типовых моделей деревьев с заданными параметрами. Это может сократить стоимость и время, затраченное на создание архитектурных макетов и игр.
Литература:
- Агафонов А. А. Построение геометрических фракталов в СКМ Maple. [Текст] / Агафонов А. А.– 2017.
- Алгебраические фракталы. Фракталы. [Электронный ресурс] — Режим обращения: http://rusproject.narod.ru/article/fractals.htm — дата обращения: — 06.03.2022
- Колмыкова, Е. А. Информатика: учебной пособие для студ. сред.проф. образования. — 2–е изд., стер. [Текст] / Е. А. Колмыкова. — М.: Издательский центр «Академия», 2017. — 416 с.







