Сигнал — это сущность, несущая информацию. В области связи сигнал представляет собой изменяющуюся во времени величину или функцию времени, и они связаны между собой набором различных уравнений, но иногда обработка сигнала искажается из-за добавления некоторого шума в информационный сигнал, и информационный сигнал становится зашумленным. Очень важно получить информацию из искаженного сигнала, поскольку мы используем фильтры. В этой статье фильтр Баттерворта предназначен для анализа сигналов, а также сравнивается с другими фильтрами. Он имеет максимально плоскую АЧХ в полосе пропускания, в противном случае пульсации в полосе пропускания отсутствуют. Чтобы соответствовать спецификации, был выбран фильтр Баттерворта 6-го порядка, поскольку он плоский в полосе пропускания и не имеет пульсаций в полосе задерживания.
Ключевые слова: фильтр Баттерворта, Фильтр Чебышева, Эллиптический фильтр.
Фильтры — это в основном схемы, которые пропускают нежелательные сигналы или удаляют шум из искаженного сигнала сообщения. Существует множество применений фильтров в области телекоммуникаций, цифровой обработки сигналов, обработки изображений, беспроводной связи и т. д. В области цифровой обработки сигналов основной функцией фильтра является удаление нежелательных компонентов из зашумленного сигнала [1]. Предположим, вы отправляете сигнал сообщения от источника к месту назначения, прежде чем сигнал достигнет места назначения, к вашему сигналу сообщения добавляется некоторый шум, поэтому шум искажает сигнал сообщения. Фильтр может использоваться для отделения шума от исходного сигнала сообщения. Например, к звуковому сигналу добавляется речевой сигнал, генерируемый преобразователем, и из-за плохой работы устройства шум, создаваемый оборудованием, поэтому мы применяем фильтр к речевому сигналу [2]. Цифровая обработка сигналов требует цифровых фильтров для получения нужных сигналов. Поэтому необходимо уменьшить шум цифрового сигнала. В этой статье мы сравним отклик фильтра Баттерворта с фильтром Чебышева и эллиптическим фильтром; эта статья будет полезна читателю благодаря подробному обсуждению ключевых аспектов конструкции фильтра Баттерворта.
Фильтр Баттерворта
Фильтр Баттерворта был впервые разработан британским инженером Стивеном Баттервортом. Фильтры Баттерворта, имеющие постоянное усиление или максимально плоскую АЧХ в полосе пропускания и уровень затухания -3 дБ и -20 дБ [3]. Аналоговая конструкция фильтра Баттерворта намного проще, чем у других фильтров, таких как Чебышев и Эллиптический. Таким образом, когда Баттерворт проектирует в аналоговой области или в s-плоскости, его легко преобразовать в цифровой фильтр или z-плоскость. В фильтре Баттерворта с увеличением порядка сохраняется основная форма, тогда как фильтры других типов, такие как Чебышевский и эллиптический, не могут поддерживать формы более высокого порядка. Фильтр Баттерворта математически определяется двумя параметрами: один — это частота среза, а другой — количество полюсов. Фазовая линейность фильтра Баттерворта лучше, чем у фильтра Чебышева. Другими словами, групповая задержка более постоянна по отношению к частоте. Это означает, что скорость искажения формы волны фильтра Баттерворта намного ниже, чем у других фильтров [4]. В основном фильтры Баттерворта используются в качестве отслеживающих высокочастотных фильтров нижних частот, сглаживающих фильтров и фильтров сглаживания. Типичный отклик фильтра нижних частот Баттерворта показан на рисунке 1.
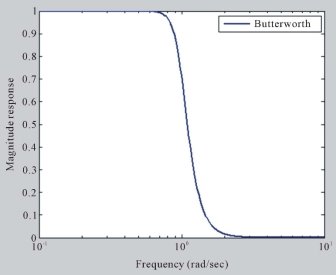
Рис. 1. Частотная характеристика фильтра нижних частот Баттерворта
Фильтр Чебышева
Название фильтра Чебышева происходит от многочленов Чебышева в честь Пафнутия Чебышева. Фильтры Чебышева могут быть аналоговыми или цифровыми фильтрами. Чебышев бывает двух типов: один называется Чебышев Тип-I, а другой называется Чебышев Тип-II. Фильтр Чебышева типа I имеет более крутой наклон и большую пульсацию в полосе пропускания, но пульсации в полосе задержания типа II. Чебышев минимизирует погрешность между идеальной и реальной характеристиками фильтра, но в полосе пропускания присутствуют пульсации. Благодаря этому свойству Чебышев имеет меньший отклик в полосе пропускания и более неравномерный отклик в полосе задерживания. В фильтре Чебышева фазовая характеристика плохая [5]. На рис. 2 показана АЧХ фильтра нижних частот Чебышева разного порядка. Если сравнивать Чебышева с Баттервортом, то можно добиться более резкой полосы перехода между полосой пропускания и полосой задерживания. Фильтр Чебышева имеет более высокую скорость выполнения и меньшие абсолютные ошибки. На рис. 3 показана частотная характеристика фильтра нижних частот Чебышева II типа.
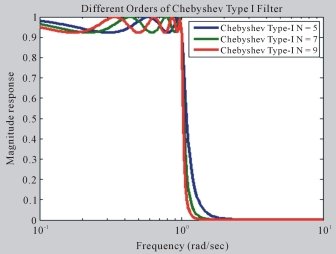
Рис. 2. Частотная характеристика фильтра Чебышева I типа
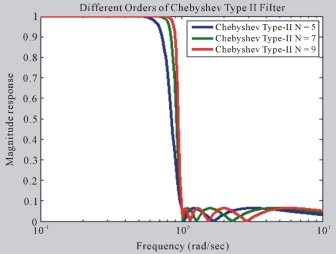
Рис. 3. Частотная характеристика фильтра Чебышева II типа
Эллиптический фильтр
Эллиптический фильтр также иногда называют фильтром Кауэра в честь Вильгельма Кауэра. В цифровой обработке сигналов его также называют фильтром Золотарева в честь Егора Золотарева. В этом типе фильтра равномерная пульсация в полосе пропускания, а также в полосе задерживания. Количество пульсаций регулируется в каждой полосе. Количество пульсаций, присутствующих в каждой полосе, показано на рисунке 4. Эллиптический фильтр, обладающий таким свойством, что если пульсации в полосе задерживания приближаются к нулю, то он действует как фильтр Чебышева I типа, если пульсации в полосе пропускания приближаются к нулю, чем он действует как фильтр Чебышева типа II, наконец, оба значения полосы пропускания и полосы задерживания приближаются к нулю, затем он действует как фильтр Баттерворта [6].
Передаточная функция фильтра Баттерворта
Конструкция фильтра нижних частот Баттерворта с помощью пассивных элементов, таких как R, L и C, и величина передаточной функции приведены ниже.
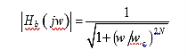
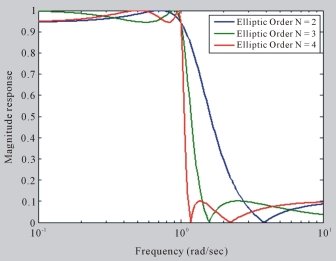
Рис. 4. Частотная характеристика эллиптического фильтра
В приведенном выше отклике фильтра по мере увеличения значения N фильтр больше похож на отклик кирпичной стены. Чтобы добиться большей точности фильтра, чем увеличить порядок фильтра, чтобы получить максимальную характеристику нижних частот. Важный момент, который следует отметить на рисунке 5, заключается в том, что в полосе пропускания, а также в полосе задерживания, как и в других фильтрах, нет пульсаций, и если мы увеличим порядок N, то переходная полоса также уменьшится, насколько это возможно.
Цифровая реализация фильтра Баттерворта
Фильтр Баттерворта легко проектируется из аналоговой области или преобразования Лапласа в цифровую область с использованием Z-преобразования. Прежде всего мы вычисляем передаточную функцию аналогового фильтра Баттерворта; его передаточная функция обычно находится в s-области и, наконец, применяет преобразование импульсной инвариантности или билинейное преобразование, отклик Баттерворта в цифровой форме.
Сходство Баттерворта с другими фильтрами
Вот различные сигналы, показывающие частотную характеристику фильтров нижних частот на рисунке 5.
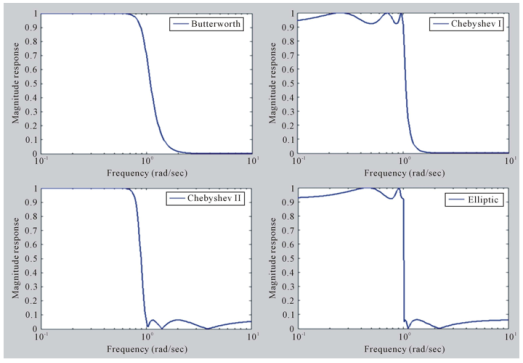
Рис. 5. Сравнение Баттерворта с другими фильтрами
Первый — это изображение фильтра нижних частот Баттерворта, которое является гладким и не имеет волнистости в полосе пропускания. В этом фильтре время перехода максимальное, если вы увеличиваете порядок фильтра, его отклик похож на форму кирпичной стены. Те же отклики показаны на рисунке 6. Далее следует фильтр Чебышева типа I, не имеющий пульсаций в полосе задерживания и с некоторыми пульсациями в полосе пропускания, затем фильтр нижних частот Чебышева типа II, не имеющий пульсаций в полосе пропускания и с некоторыми пульсациями в полосе задерживания. Наконец, у эллиптического фильтра рябь присутствует в обеих полосах, но переходная полоса эллиптического фильтра минимальна, чем у других фильтров [8]. В Matlab доступна панель инструментов функции фильтрации [9], а также напишите код Matlab, чтобы нарисовать другой отклик фильтра.
Программа для проектирования фильтра нижних частот Баттерворта смоделирована в MATLAB 7.
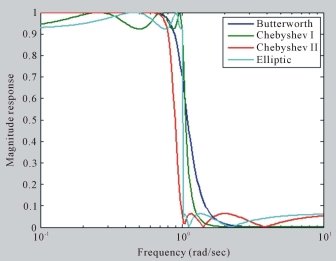
Рис. 6. Сравнение Баттерворта с другими фильтрами в моделировании MATLAB
Выходные графики показаны на рис. 6, что указывает на то, что фильтр Баттерворта лучше справился с удалением низкочастотных составляющих, чем фильтр Чебышева и эллиптический фильтр [10]. В таблице 1 приведены результаты расчетов коэффициентов фильтра Баттерворта нижних частот для порядка от N от 1 до 6.
Заключение
В этой статье мы описали, что фильтр нижних частот Баттерворта имеет максимально плоскую амплитудную характеристику в полосе пропускания, и в полосе пропускания отсутствуют пульсации. Время перехода контролируется, когда вы увеличиваете порядок фильтра, в противном случае, чтобы получить точность фильтра. Фильтр Баттерворта сравнивается с другими фильтрами, такими как фильтры Чебышева-I, Чебышева-II и эллиптические фильтры, которые дают лучший отклик и, наконец, рисуют все отклики фильтра в Matlab 7 для сравнения откликов фильтров. Наконец, сравнение фильтра Баттерворта очень простое и требует низкого порядка точности, но мы не можем достичь удовлетворительных результатов, поэтому здесь я предложил другие методы или даже методы автоматического фильтра нижних частот, доступные для создания различных откликов фильтра нижних частот, которые адаптируются к задаче.
Литература:
- Попов В. И. Основы сотовой связи стандарта GSM. Москва: Эко-Трендз, 2005, 296 с.
- Слюсар В. Антенны PIFA для мобильных средств связи. Электроника: НТБ, 1/2007, 64–74 с., 2007.
- Fujimoto K., James J. R. Mobile Antenna Systems Handbook. London: Artech. House, Inc., 1994, 710 p.
- Fujimoto K., Morishita H. Modern Small Antennas. New York: Cambridge University Press, 2014, 473 p.
- Gibson J. D. The Mobile Communication Handbook. New York: IEEE Press, 1999
- http://www.electronics-tutorials.ws/filter/filter_8.html







