Статья посвящена исследованию алгоритмов для генерации псевдослучайных чисел. Необходимо описать алгоритм, программная реализация которого позволит осуществить ввод количества чисел и выполнить их генерацию.
Ключевые слова : случайность, ключ, ГПСЧ, ЛКГ.
Понятие «случайности» является важнейшим во многих областях информатики, включая моделирование, криптографию, статистику и алгоритмы, использующие искусственно сгенерированные значения. В криптографии случайность обычно используется для генерации ключей, векторов инициализации (IV) или одноразовых номеров для алгоритма шифрования. Ключ является неотъемлемой частью в любом способе обеспечения безопасности, поскольку современные криптографические алгоритмы построены на том принципе, что безопасность системы полностью зависит от ключа, а не от конструкции самой системы. Это означает, что криптографическая стойкость всех современных алгоритмов и протоколов безопасности выражается в виде размера ключа, который злоумышленник должен угадать, прежде чем нарушить безопасность системы.
Такая сила неявно предполагает, что злоумышленник не знает количества битов исходного используемого ключа. Эффективная сила алгоритма снижается, когда обнаруживаются более совершенные атаки на него и можно получить больше битов ключа, просматривая часть выходных данных. С повышением скорости вычислений и появлением квантовых вычислений всегда существует надвигающаяся опасность атаки частичного сокращенного полного перебора на такие системы, если часть ключа может быть угадана.
Истинную «случайность» невозможно создать математически. Пусть существует функция f(x), которая выдает случайное число для заданных входных данных x после серии операций над x и с некоторыми фиксированными, четко определенными константами. Функция обладает замечательным свойством — она выдает различные данные каждый раз, когда вводится одна и та же константа. Интуитивно можно предположить, что такой функции не существует, и это связано с тем, что f(x) полностью детерминирована по своей природе. Если x и определение f(x) известны, то для данного входа x или ряда входов (которые могут включать время в качестве параметра) f(x) всегда будет давать один и тот же результат. Следовательно, алгоритмы, представляющие собой набор инструкций и детерминированные по своей природе, не могут обеспечить истинную случайность. Это прекрасно резюмировал Джон фон Нейман в своей знаменитой цитате: «каждый, кто использует арифметические методы генерации случайных чисел, безусловно, грешит» [10].
Чаще всего для того, чтобы получить некую «случайность», используются следующие методы:
- Интеграция физического источника случайности, такого как тепловой шум в резисторе, в разрабатываемую систему. В таких системах скорость генератора может быть проблемой, которая может существенно снизить общую производительность системы.
- Использование криптографически защищенного генератора псевдослучайных чисел (англ. Cryptographically Secure Pseudorandom number generator, CSPRNG) в качестве автономного генератора или с физическим источником в качестве генератора начального числа для разрабатываемой системы.
Чтобы генераторы псевдослучайных чисел (ГПСЧ) были криптографически устойчивыми, они должны удовлетворять двум условиям:
- Статистическая разница: вероятность обнаружения различий между статистическими свойствами последовательности ГПСЧ по сравнению со свойствами действительно случайной последовательности с помощью любого алгоритма с полиномиальным временем не должна быть значительно больше 0,5.
- Предсказание следующего бита: зная первые k битов последовательности, шанс предсказания следующего, то есть (k + 1)-го, бита для любого алгоритма с полиномиальным временем не должен быть значительно больше 0,5.
Стоит отметить, что оба условия должны выполняться одновременно, и одно не влечет за собой другое.
В качестве альтернативы «настоящим» случайным числам еще один метод генерации случайных чисел включает в себя вычислительные алгоритмы, которые могут давать псевдослучайные результаты. В этом случае полученные конечные результаты фактически полностью определяются начальным значением, также известным как ключ. Следовательно, зная значение ключа и то, как работает алгоритм, можно было бы воспроизвести эти, казалось бы, случайные результаты. Генераторы случайных чисел этого типа часто называют генераторами псевдослучайных чисел, и в результате они выдают псевдослучайные числа. Несмотря на то, что этот тип генератора обычно не собирает данные из источников естественной случайности, такой сбор ключей можно сделать возможным, когда это необходимо.
ГПСЧ быстрее, чем истинные генераторы случайных чисел. Из-за своей детерминированной природы они полезны, когда нужно воспроизвести последовательность случайных событий. Это очень помогает, например, при тестировании кода. С другой стороны, истинные генераторы не являются периодическими и лучше работают в чувствительных к безопасности ролях, таких как шифрование. При прочих равных условиях для предсказания и взлома ГПСЧ с более длинным периодом потребуется больше ресурсов компьютера.
Программа выполняет код, руководствуясь набором правил, которым необходимо следовать. Для ГПСЧ в целом эти правила вращаются вокруг следующих принципов:
- Принять некоторый начальный входной номер, который является ключом.
- Применить это начальное число в последовательности математических операций, чтобы получить результат. Этот результат является случайным числом.
- Использовать полученное случайное число в качестве начального значения для следующей итерации.
- Повторить процесс, чтобы эмулировать случайность.
Начиная с ранних работ фон Неймана, общий метод получения псевдослучайных чисел строится на некоторой (детерминированной) функции, которая итеративно применяется к (случайному) начальному числу и пытается аппроксимировать результат равномерно распределенных независимых случайных испытаний. На сегодняшний день существует очень много таких генераторов псевдослучайных чисел, которые соответствуют различным требованиям к качеству и сложности случайных чисел. Высокоэффективные алгоритмы, требующих больших затрат памяти, делятся на два вида — легковесные генераторы псевдослучайных чисел общего назначения и сильные (более сложные и криптозащищенные) генераторы. Говоря нестрогим языком, сильные ГПСЧ имеют длительный период (число значений, которое они генерируют перед повторением) и статистически равномерное распределение генерируемых значений (биты 0 и 1 появляются с одинаковой вероятностью независимо от предыдущих значений). Это свойство имеет большое значение в криптографии, поскольку последовательности со слишком коротким периодом могут наблюдаться, записываться и повторно использоваться злоумышленником, в то время как последовательности с длинными периодами вынуждают противника выбирать альтернативные методы атаки. В статье будут рассмотрены шесть популярных генераторов — три типа сильных генератора и три легковесных.
ГПСЧ Fortuna относится к криптографическим генераторам [5] и был разработан для преодоления потребности в оценках энтропии, которые имеют тенденцию быть неточными [3]. Внутри алгоритм Fortuna поддерживает пулы энтропии (генераторы шума), из которых выполняется периодическое заполнение с повторениями. Пулы заполняются из различных доступных источников энтропии, значения которых распределяются между этими пулами. Накопление энтропии осуществляется путем хэширования состояния внутреннего генератора и одного пула энтропии за раз с использованием функции SHA-256. Этот механизм позволяет генерировать случайные последовательности неограниченного периода, однако он не в состоянии преодолеть требования к надлежащим источникам энтропии для заполнения генератора и для обновления пулов энтропии, поэтому существуют некоторые потенциально побочные эффекты повторного заполнения. Конечные блоки псевдослучайного вывода генерируются блочным шифром AES-128 в режиме счетчика.
ГПСЧ SHA256 — это генератор, который выдает криптографически стойкие случайные числа. Оригинальный механизм этого генератора был представлен в FIPS 186–1 [11] и проанализирован в работе [2]. Выходные данные генерируются путем хэширования состояния внутреннего генератора, которое после этого обновляется путем линейного преобразования хэша. Этот метод является преемником SHA1, который до недавнего времени считался безопасным [4], но со временем устарел. Причины устаревания в основном связаны с ошибкой заполнения в Java и с тем, что NIST не рекомендует базовую хеш-функцию SHA-1, поскольку в работах [13, 14] была обнаружена атака, которая уменьшила количество попыток полного перебора, необходимых для создания коллизий состояний, с 2 80 до 2 63 операций. По этой причине ГПСЧ SHA256 заменяет функцию вывода SHA-1 на SHA-256. Генератор ограничивается одним хэш-вычислением на блок, что делает его вычислительно эффективным. Чтобы добавить полную прямую секретность, NIST разработал набор улучшенных и стандартизированных генераторов случайных битов [1]. Стоит отметить, что стандарты для генераторов от NIST также являются наиболее действенным способом их тестирования. Набор тестов NIST нацелен в основном на условие (а), необходимое для сложных систем, и тесты, как правило, дают P-значение. Это P-значение сравнивается с уровнем значимости (𝛼), который определяется тестировщиком. Чаще всего это значение 𝛼 принимается равным 0,01. Если для данного теста P-значение последовательности меньше 𝛼, говорят, что последовательность не прошла тест.
Вихрь Мерсенна является широко используемым генератором, который, как известно, в своей версии по умолчанию не является безопасным [9], даже несмотря на то, что криптозащищенные варианты были исследованы в значительной степени. Однако серьезными преимуществами этого алгоритма являются длительный период и сравнительно быстрое выполнение операций, поскольку при генерации псевдослучайных чисел не требуется умножения и деления. Версия вихря Мерсенна, доступная на многих языках программирования, MT19937, имеет впечатляющий период 2 19937– 1. Сила MT19937 также заключается в том, что одно сгенерированное им 32-битное значение нельзя использовать для предсказания последующего 32-битного значения. Это обеспечивает определенную степень непредсказуемости. Но, несмотря на это, алгоритм MT19937 отслеживает свое состояние всего в 624 32-битных значениях. Если бы злоумышленник смог собрать все эти последовательные значения, то всю последовательность можно было бы реконструировать. Эта функция не является специфической для вихря Мерсенна — большинство ГПСЧ имеют механизм состояния, который используется для генерации следующего значения в последовательности. Знание состояния фактически ставит под угрозу предсказуемость последовательности, и это еще один пример того, как неправильное использование ГПСЧ может привести к его компрометации. Следует также отметить, что у вихря Мерсенна есть легковесная версия, которая адаптируется к ограничениям ресурсов что значительно снижает требования к буферу за счет сокращения продолжительности периода. Генератор представляет собой, скорее, уменьшенное, эффективное по памяти резервное решение полного вихря Мерсенна [15].
Генератор Xorshift принадлежит к семейству генераторов регистров сдвига с линейной обратной связью, которые не являются криптографически безопасными. Он известен своей эффективностью использования ресурсов, поскольку ограничивается простыми операциями вроде исключающего «ИЛИ» и битового сдвига. Генераторы Xorshift являются одними из самых быстрых криптографически нестойких генераторов случайных чисел, а их реализация не предполагает больших объёмов кода или сохраняемого состояния системы, но они требуют тщательного подбора начальных параметров, для получения более длинных периодических последовательностей. В работе [8] был предложен набор расширенных ГПСЧ Xorshift с увеличенной длиной периода и улучшенными статистическими свойствами. Производными генераторами являются Xorshift64 и Xorshift128. Xorshift64 состоит из 64-битного состояния и применяет постоянное умножение к выходу для скремблирования битов. Xorshift128 требует 128-битного состояния, хотя выводит только 64-битные значения за цикл. В отличие от Xorshift64 он добавляет к выходным данным два последовательных значения состояния в качестве нелинейного преобразования. Пример случайного распределения Xorshift128 приведен на рисунке 1.
Линейные конгруэнтные генераторы (ЛКГ) используют другой подход к созданию числовых последовательностей. Они предшествовали Интернету, существуя с 1948 года. Простые алгоритмы ЛКГ создают последовательность из формулы, основанной на постоянном множителе, постоянном аддитивном значении и постоянном модуле. Формула (1) описывает метод генерации ЛКГ.
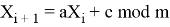
где
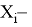
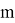
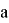
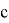
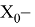
как seed (принимает значения от 0 до m — 1).

Рис. 1. Пример случайного распределения Xorshift128
При a = 1 такой метод будет называться методом аддитивного сравнения, а при c = 0 — мультипликативным конгруэнтным методом. При c=0 генерируемые числа будут иметь меньший период, чем при c ≠ 0, но при определенных условиях можно получить период длиной m — 1, если m представляет собой простое число. Следует отметить, что хоть период ЛКГ намного короче, чем у MT19937, для эффективной атаки не требуется наблюдения более чем за несколькими последовательными значениями — для взлома требуется менее двух десятков последовательных выборок из последовательности. Говоря простым языком, атака определяет модуль m в ЛКГ путем нахождения наибольшего общего делителя (НОД) объемов параллелепипедов, описываемых векторами, взятыми из последовательности ЛКГ.
Два наиболее популярных ГПСЧ ЛКГ — это методы Кнута и Парка-Миллера. Алгоритм Парка-Миллера, также называемый генератором случайных чисел Лемера, работает в мультипликативной группе целых чисел. Он известен уже несколько десятилетий [12]. Мотивированный целью своего создателя разработать легкий генератор, который ограничивается 32-битной арифметикой без операций деления, он неоднократно подвергался критике за свои статистические свойства. Генератор имеет период или 2 31 − 1, и он может производить всего лишь 31 псевдослучайный бит в течение каждого цикла. Метод генерации описывается формулой (2).
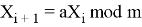
причем
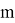
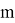
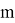
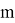
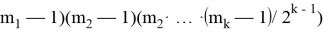
ЛКГ Кнута — это широко используемый линейный конгруэнтный генератор, который не требует больших вычислительных ресурсов и исследуется десятилетиями. Он реализован в ряде программных проектов, а исходный код доступен в различных стандартных библиотеках. В генераторе используется множитель, полученный Кнутом [6], но популярные реализации отличаются от представленной Кнутом своим приращением. Кроме того, он усекает старшие значащие биты 64-битного состояния до 32-битных выходных значений из-за плохих статистических свойств младших битов в генераторах по модулю два [7].
ЛКГ, основанный на формуле (1), является самым простым примером генератора случайных чисел. Это один из старейших и самых известных методов. Алгоритм подпрограммы обработки (метода LCG, выполняющего генерацию очередного псевдослучайного числа) в виде блок-схемы приведен на рисунке 2, главной программы — на рисунке 3.
Рисунок 4 иллюстрирует пример работы программы, код которой использует алгоритмы из рисунков 2 и 3. При вводе количества чисел будут выведены все сгенерированные числа и время на генерацию в микросекундах.
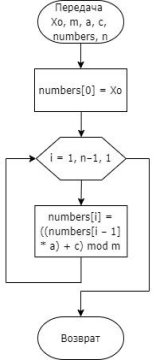
Рис. 2. Алгоритм подпрограммы LCG

Рис. 3. Алгоритм главной программы
Здесь (см. рисунок 4) в качестве начального значения выбрано время, прошедшее с 1 января 1970 года в секундах, значение модуля равно 2147483648, множителя — 214013, инкремента — 2531011. Эти значения задаются при запуске программы и не меняются в процессе ее выполнения.
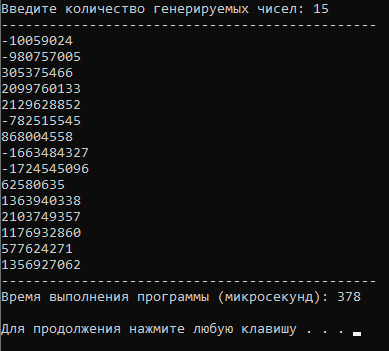
Рис. 4. Пример работы программы, реализующей алгоритм генерации псевдослучайных чисел
Таким образом, в статье были рассмотрены сильные и легковесные генераторы псевдослучайных чисел, изучены их основные свойства и механизм работы. В качестве основного метода генерации был подробно разобран ГПСЧ ЛКГ.
С появлением компьютеров разработчики осознали потребность в средствах введения случайности в компьютерные программы. Однако, как это ни удивительно, трудно заставить компьютер что-то делать случайно, так как компьютер слепо следует заданным инструкциям и поэтому полностью предсказуем. Невозможно генерировать действительно случайные числа без специализированных аппаратных устройств, поэтому генераторы псевдослучайных чисел (ГПСЧ) — это класс методов, разработанных для генерации случайных чисел с помощью компьютера.
ГПСЧ относятся к типу алгоритмов, использующих математические формулы для создания последовательностей случайных чисел. ГПСЧ генерируют последовательность чисел, аппроксимирующих свойства случайных чисел. Многие числа генерируются за короткое время и могут быть воспроизведены позже, если известна начальная точка последовательности. Следовательно, числа детерминированы и эффективны.
ГПСЧ присущи такие характеристики, как эффективность (ГПСЧ может выдавать много чисел за короткое время и лучше всего подходи для приложений, которым они требуются), детерминизм (последовательность чисел может быть воспроизведена позже, если известна начальная точка последовательности, что удобно в тех случаях, когда нужно снова воспроизвести ту же последовательность чисел на более позднем этапе) и периодичность (последовательность в конечном итоге будет повторяться, однако это происходить с настолько большим периодом), что его можно игнорировать для большинства практических целей.
ГПСЧ подходят для приложений, где требуется много случайных чисел и где полезно, чтобы одна и та же последовательность могла быть легко воспроизведена. Популярными примерами таких приложений являются приложения для имитации и моделирования. ГПСЧ не подходят для приложений, где важно, чтобы числа были действительно непредсказуемыми, например, для шифрования данных и азартных игр.
Литература:
- Barker, E., Kelsey, J. 2012. Recommendation for Random Number Generation Using Deterministic Random Bit Generators. Special Publication NIST SP 800–90A. National Institute of Standards & Technology, Gaithersburg, MD, United States.
- Desai, A., Hevia, A. 2002. A Practice-Oriented Treatment of Pseudorandom Number Generators. In EUROCRYPT '02: Advances in Cryptology (LNCS), Vol. 2332. Springer, Berlin, Heidelberg, 368–383
- Ferguson, N., Schneier, B., Kohno, T. 2010. Cryptography Engineering: Design Principles and Practical Applications. Wiley Publishing, Indianapolis, Indiana, USA
- Galbreath, N. 2002. Cryptography for Internet and Database Applications: Developing Secret and Public Key Techniques with Java. Wiley Publishing, Indianapolis, Indiana, USA.
- Killmann, W., Schindler, W. 2011. A proposal for: Functionality classes for random number generators. Technical Report AIS 20 / AIS 31. BSI, Bonn, Germany. 1–133 pages.
- Knuth, D. 2009. The Art of Computer Programming (Second Edition). Addison Wesley, Reading, MA, USA
- Marsaglia, G. 1968. Random Numbers Fall Mainly in the Planes. Proc. of the National Academy of Sciences 61, 1 (1968), 25–28.
- Marsaglia, G. 2003. Xorshift RNGs. Journal of Statistical Software, Articles 8, 14 (2003), 1–6.
- Matsumoto, M., Nishimura, T. 1998. Mersenne Twister: A 623-dimensionally Equidistributed Uniform Pseudo-Random Number Generator. ACM Trans. Model. Comput. Simul. 8, 1 (1998), 3–30
- Neumann, J. 1951. Various Techniques Used in Connection with Random Digits. J. Res. Nat. Bur. Stand. Appl. Math. Series 5 (1951), 768–770
- NIST. 1998. Digital Signature Standard. Federal Information Processing Standards 186–1. National Institute of Standards & Technology, Gaithersburg, MD, US.
- Park, S., Miller, K. 1988. Random Number Generators: Good Ones Are Hard to Find. Commun. ACM 31, 10 (1988), 1192–1201.
- Stevens, M., Bursztein, E., Karpman, P. 2017. The First Collision for Full SHA-1. In Advances in Cryptology (CRYPTO ’17). Springer, Cham, Switzerland, 570–596
- Wang, X., Lisa, Y., Yu, H. 2005. Finding Collisions in the Full SHA-1. In CRYPTO '05; Proceedings of the 25th Annual International Conference on Advances in Cryptology. Springer-Verlag, Berlin, Heidelberg, 17–36.
- Saito, M., Matsumot, M. 2011. Tiny Mersenne Twister (TinyMT): A small-sized variant of Mersenne Twister. Режим доступа: http://www.math.sci.hiroshima-u.ac.jp/~m-mat/MT/TINYMT (дата обращения: 23.07.2022)







