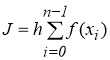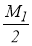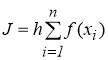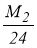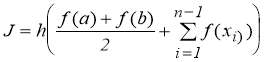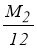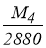Сравнение точности методов численного интегрирования на примере элементарных функций



В статье авторы проводят вычислительный эксперимент, посредством которого производится сравнение возможностей различных методов численного интегрирования на примере элементарной функции.

Ключевые слова: численное интегрирование, точность, приближённое значение интеграла, интерполяция, методы численного интегрирования.

Поскольку аналитическое значение интеграла зачастую получить довольно сложно или вообще невозможно, применение численных методов в интегрировании является актуальной задачей. При этом различные методы численного интегрирования имеют разную точность. В связи с этим в данной работе проведен вычислительный эксперимент для определения и сравнения точности пяти методов интегрирования на примере элементарной функции, точное значение интеграла которой известно.

Существует много сложных и неберущихся интегралов, в таких случаях используют численное интегрирование для нахождения приблизительного значения. Задача численного интегрирования состоит в замене исходной подынтегральной функции некоторой аппроксимирующей функцией (обычно полиномом).

Численное интегрирование применяется, когда:

– сама подынтегральная функция не задана аналитически, а например, представлена в виде таблицы значений;

– аналитическое представление подынтегральной функции известно, но её первообразная не выражается через аналитические функции.

Все основные способы численного интегрирования сводятся к интерполяции функции по ее значениям в узловых точках f ( x _i ) и интегрированию интерполяционного многочлена. При этом значение интеграла получается приближенно равным сумме

.(1)

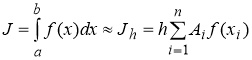
При различном выборе A _i и x _i получаются различные квадратурные формулы. Каждая из них обладает некоторой погрешностью , которую можно оценить следующим образом:

(2)

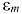
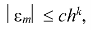
где c >0 — некоторая постоянная, не зависящая от h (зависящая от a , b , вида f ( x ) и метода интегрирования), k -некоторое целое число, называемое порядком точности метода. Чем больше k , тем быстрее убывает погрешность при уменьшении h .

Предлагается рассмотреть квадратурные формулы Ньютона-Котеса, к которым, в частности, относятся формулы прямоугольников (левых, правых и симметричных), трапеций, парабол. В таблице 1 представлены эти формулы и значения констант для оценки погрешности по формуле (2). В таблице обозначено

, f ^{( j )} ( x ) — j -ая производная f ( x ).

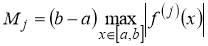
Таблица 1

Квадратурные формулы различных методов

№	Название метода	Квадратурная формула	c	k
1	Левых прямоугольников			1
2	Правых прямоугольников			1
3	Симметричных прямоугольников			2
4	Трапеций			2
5	Парабол			4

Суть методов заключается в разбиении площади под кривой на площадь определенных фигур, а интеграл на всем отрезке интегрирования считается как сумма этих частичных интегралов.

При методах прямоугольников вместо площади криволинейной фигуры вычисляются площади прямоугольников. В методе левых прямоугольников берется площадь прямоугольника по левой границе (рис. 1), в методе правых прямоугольников — по правой (рис. 2), в методе средних (рис. 3) — по значению функции в середине отрезка. Это интерполяционные многочлены нулевой степени.

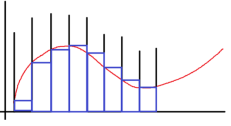
Рис. 1. Метод левых прямоугольников

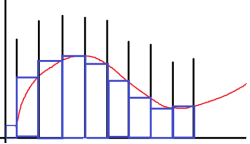
Рис. 2. Метод правых прямоугольников

Рис. 3. Метод серединных прямоугольников

Метод трапеций осуществляет интерполяцию многочлена первой степени. При методе трапеций вместо площади криволинейной фигуры вычисляются площади трапеций (рис. 4).

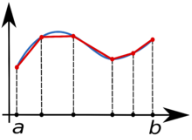
Рис. 4. Метод трапеций

В методе парабол определяется площадь под параболой. Сама парабола строится через три точки — два значения функции в узловые точках и одно значение между ними в середине отрезка (рис. 5). Метод парабол реализует интерполяцию многочлена второй степени.

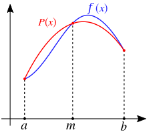
Рис. 5. Метод парабол

В данной работе был разработан алгоритм и программа вычисления интеграла выбранными методами для сравнения их точности. В качестве отладочного примера выбрана функция f ( x ) =е ^х (рис.6) и отрезок интегрирования [0,1].

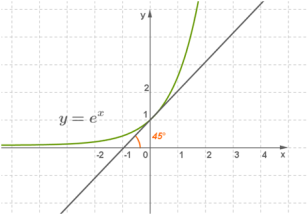
Рис. 6. График экспоненты y= е ^х

Результаты работы программы для вычисления приближенных значений интеграла при увеличении количества частичных отрезков вдвое начиная с n= 1, представлены в таблице 2.

Таблица 2

Значения интеграла, полученные разными методами численного интегрирования

n	J1	J2	J3	J4	J5
1	1	2.71828182845905	1.64872127070013	1.85914091422952	1.71886115187659
2	1.32436063535006	2.18350154957959	1.70051271665021	1.75393109246483	1.71831884192175
4	1.51243667600014	1.9420071331149	1.71381527977109	1.72722190455752	1.7182841546999
8	1.61312597788561	1.82791120644299	1.71716366499569	1.7205185921643	1.71828197405189
16	1.66514482144065	1.77253743571934	1.71800219205266	1.71884112857999	1.71828183756177
32	1.69157350674665	1.745269813886	1.71821191338386	1.71842166031633	1.71828182902802
64	1.70489271006526	1.73174086363493	1.71826434931686	1.71831678685009	1.71828182849461
128	1.71157852969106	1.7250026064759	1.71827745865016	1.71829056808348	1.71828182846127
256	1.71492799417061	1.72164003256303	1.71828073600537	1.71828401336682	1.71828182845918
512	1.71660436508799	1.7199603842842	1.71828155534553	1.71828237468609	1.71828182845905
1024	1.71744296021676	1.71912096981487	1.71828176018066	1.71828196501581	1.71828182845905
2048	1.71786236019871	1.71870136499776	1.71828181138945	1.71828186259824	1.71828182845905
4096	1.71807208579408	1.71849158819361	1.71828182419165	1.71828183699384	1.71828182845905
8192	1.71817695499286	1.71838670619263	1.7182818273922	1.71828183059274	1.71828182845905
16384	1.71822939119253	1.71833426679241	1.71828182819233	1.71828182899247	1.71828182845905
32768	1.71825560969243	1.71830804749237	1.71828182839237	1.7182818285924	1.71828182845905
65536	1.7182687190424	1.71829493794237	1.71828182844238	1.71828182849238	1.71828182845905
131072	1.71827527374239	1.71828838319237	1.71828182845488	1.71828182846738	1.71828182845905
262144	1.71827855109863	1.71828510582363	1.718281828458	1.71828182846113	1.71828182845905
524288	1.71828018977832	1.71828346714081	1.71828182845878	1.71828182845957	1.71828182845905
1048576	1.71828100911855	1.7182826477998	1.71828182845898	1.71828182845918	1.71828182845905
2097152	1.71828141878877	1.71828223812939	1.71828182845903	1.71828182845908	1.71828182845905
4194304	1.7182816236239	1.71828203329421	1.71828182845904	1.71828182845905	1.71828182845905
8388608	1.71828172604147	1.71828193087663	1.71828182845904	1.71828182845905	1.71828182845905

Первый столбец n — количество разбиений отрезка, последующие столбцы J1-J5 представляют собой значение интеграла, полученного с помощью численного интегрирования методами левых, правых, средних прямоугольников, трапеций и парабол соответственно.

Для формирования выводов об оценке погрешности преобразуем полученную таблицу вычисленных приближенных значений, скорректировав каждое из них вычитанием из него точного результата интегрирования функции экспоненты на промежутке [0,1], равного числу 1,718281828459045. Получим таблицу абсолютных погрешностей значений интеграла при разных n (таблица 3).

Таблица 3

Абсолютные погрешности значений интеграла для разных методов

n	J1	J2	J3	J4	J5
1	0.718281828459045	-1	0.0695605577589169	-0.140859085770478	-0.00057932341754788
2	0.393921193108981	-0.465219721120542	0.017769111808837	-0.0356492640057803	-3.70134627020876e-05
4	0.205845152458909	-0.223725304655852	0.0044665486879581	-0.00894007609847164	-2.3262408518146e-06
8	0.105155850573434	-0.109629377983947	0.00111816346335816	-0.00223676370525677	-1.45592846813639e-07
16	0.0531370070183959	-0.0542556072602945	0.000279636406384778	-0.000559300120949303	-9.10272658237368e-09
32	0.0267083217123903	-0.0269879854269548	6.99150751859025e-05	-0.000139831857282262	-5.68970152567926e-10
64	0.0133891183937881	-0.0134590351758845	1.74791421817724e-05	-3.49583910481797e-05	-3.5561545028151e-11
128	0.00670329876798494	-0.00672077801685135	4.36980888248568e-06	-8.73962443320405e-06	-2.22274434101555e-12
256	0.00335383428843371	-0.00335820410398443	1.09245367909414e-06	-2.1849077753587e-06	-1.39056951717342e-13
512	0.0016774633710564	-0.00167855582515267	2.73113510826026e-07	-5.46227048132605e-07	-8.82692356707349e-15
1024	0.000838868242283615	-0.000839141355820921	6.8278383296436e-08	-1.36556768652856e-07	-6.86733656052319e-16
2048	0.000419468260333455	-0.000419536538718813	1.7069596071036e-08	-3.41391926788606e-08	-1.79001778677357e-16
4096	0.000209742664964763	-0.000209759734561371	4.26739893064337e-09	-8.53479830374964e-09	-1.47451495458029e-16
8192	0.000104873466181847	-0.00010487773358122	1.06684962676139e-09	-2.1336996863363e-09	-1.44307309157821e-16
16384	5.24372665157432e-05	-5.24383333657904e-05	2.66712295586731e-10	-5.33425023661709e-10	-1.44198888940572e-16
32768	2.62187666140096e-05	-2.62190333267571e-05	6.66779658830413e-11	-1.33356373795308e-10	-1.4734307524078e-16
65536	1.31094166459884e-05	-1.3109483324395e-05	1.66693796353062e-11	-3.33392032514021e-11	-1.4810201676152e-16
131072	6.55471665769172e-06	-6.55473332749994e-06	4.16724001226637e-12	-8.33490416442262e-12	-1.4137996329211e-16
262144	3.27736041244825e-06	-3.27736458014774e-06	1.04168984636083e-12	-2.08384980278364e-12	-1.56775634141404e-16
524288	1.63868072709252e-06	-1.63868176920542e-06	2.60295040729885e-13	-5.21056396814157e-13	-1.55474591534421e-16
1048576	8.19340493677951e-07	-8.19340754470966e-07	6.49589973825138e-14	-1.30396561603963e-13	-1.59594559789866e-16
2097152	4.09670279317986e-07	-4.09670344756526e-07	1.60835971277362e-14	-3.2719270001702e-14	-1.84097528888039e-16
4194304	2.04835147790726e-07	-2.0483516424653e-07	4.01848693210027e-15	-8.22790186677524e-15	-6.36426675248991e-17
8388608	1.02417575804752e-07	-1.02417580213877e-07	9.49652682880053e-16	-2.20450827731478e-15	-1.01806583996389e-16
16777216	5.12087883066748e-08	-5.12087897025851e-08	4.71627945031194e-17	-6.98009358646168e-16	-2.0122792321331e-16

При анализе полученной таблицы значений скорректированных результатов приближенного вычисления можно сделать следующие выводы:

– При большом шаге разбиения (малом количестве интервалов) наибольшей степенью точности обладает метод Симпсона.

– Методы правых и левых прямоугольников имеют в значительной степени низкую точность. Результат их отклонения от точного значения интеграла, при максимальном количестве отрезков ( n =16777216) укладывается в промежуток между значениями погрешности, которые мы получили методом Симпсона при количестве частичных отрезков 8 и 16.

– Погрешности, которые мы получили при расчетах методами левых и правых прямоугольников, являются по модулю примерно равными друг другу. При устремлении количества частичных отрезков в бесконечность, отношение вычисляемых этими методами значений устремляется к единице.

– Наибольшая точность в итоговых результатах исследования отмечена в методе средних прямоугольников.

– В отличие от прочих приведенных методов, метод Симпсона сокращает погрешность наиболее быстро. Однако этот метод является единственным в рассмотрении, который вышел на «плато», т. е. его точность при достижении определенного уровня в значительной степени не изменялась, в то время как остальные методы уменьшали свою погрешность более равномерно. Это связано с ограничением оптимального числа частичных отрезков в связи накоплением погрешности округления, которая снижает точность при дальнейшем увеличении n , что наблюдается в последних двух строках последнего столбца.

Таким образом, методы левых, правых, серединных прямоугольников, трапеций и парабол были применены для численного интегрирования элементарной функции. Проведенный вычислительный эксперимент позволил проанализировать точность рассмотренных методов численного интегрирования по величине отклонения результатов вычислений от точного аналитического значения интеграла и сделать выводы о возможности применения этих методов.

Литература:

1. Reliability increase of numerical data under indeterminacy condition by using of several methods / Zhitnikov V. P., Sherykhalina N. M., Muksimova R. R., Zhitnikova N. I./ Proceedings of 19-th Workshop on Computer Science and Information Technologies (CSIT’2017), Vol. 1, Baden-Baden, Germany, 2017, pp. 268–275.
2. Increasing the reliability of numerical data using several methods under conditions of indeterminacy / Zhitnikov V. P., Sherykhalina N. M., Muksimova R. R., Zhitnikova N. I./ 7th Scientific Conference on Information Technologies for Intelligent Decision Making Support (ITIDS 2019). Atlantis Press. Advances in Intelligent Systems Research, volume 166, pp. 61–68.
3. Influence of different components of data error on the result of solving identification and approximation problems / Zhitnikov V. P., Sherykhalina N. M., Muksimova R. R., Zhitnikova N. I./ IOP Conf. Ser.: Mater. Sci. Eng. 2020. Vol. 919, article no. 052016, pp. 1–7. doi:10.1088/1757–899X/919/5/052016.
4. Numerical filtration in the problems of integration and series summing / Sherykhalina N. M., Akhmadullin A. A., Gallyamutdinova K. R./ 7th All-Russian Scientific Conference on Information Technologies for Intelligent Decision Making Support (ITIDS 2020). October 6–9, Ufa — Stavropol-Khanty-Mansiysk, Russia, 2020, Vol. 2, pp. 98–102.
5. Multi-stage filtering of numerical solutions with an application to the Hele-Shaw problem / Zhitnikov V. P., Шерыхалина Н. М., Porechny S. S., Sokolova A. A. /7th All-Russian Scientific Conference on Information Technologies for Intelligent Decision Making Support (ITIDS 2020). October 6–9, Ufa — Stavropol-Khanty-Mansiysk, Russia, 2020, Advances in Intelligent Systems Research, Vol. 174, pp. 178–185.
6. Методика качественного улучшения результатов вычислительного эксперимента / Житников В. П., Шерыхалина Н. М., Федорова Г. И., Соколова A. A./ Системная инженерия и информационные технологии / Уфа, 2021, Т.3, № 1(5). С. 58–64.
7. Исследование погрешностей при решении задач для простейших уравнений математической физики итерационными методами / Житников В. П., Шерыхалина Н. М., Муксимова Р. Р./ Сиб. журн. вычисл. Мтематики / РАН. Сиб. отд-ние.–– Новосибирск, 2021. –– Т. 24, N◦ 2. –– С. 131–143. Английская версия этой статьи печатается в журнале “Numerical Analysis and Applications” N◦ 2, Vol. 14, 2021.
8. Influence of various components of errors on the results of approximation using orthogonal functions / Zhitnikov V. P., Sherykhalina N. M., Zhitnikova N. I., Muksimova R. R./ IOP Conference Series Materials Science and Engineering. 2021. Vol. 1047(1), article no. 012098, pp. 1–15.
9. Применение методов численной фильтрации в задачах интегрирования и суммирования рядов / Шерыхалина Н. М., Ахмадуллин А. А., Галлямутдинова К. Р./ Вестник УГАТУ. 2021. Т. 25, № 4(94). С 124–131.
10. Уточнение результатов решения задач численного интегрирования и суммирования ряда методом Эйткена / Шерыхалина Н. М., Галлямутдинова К. Р./ Мавлютовские чтения: материалы V Международной научнотехнической конференции Том 5: Компьютерные технологии и цифровые двойники / Уфимск. гос. авиац. техн. ун-т. — Уфа: УГАТУ, 2021. — С.197–201. ISBN 978–5–4221–1464–1.