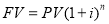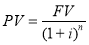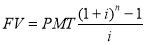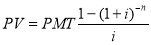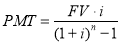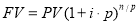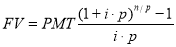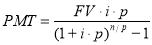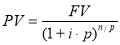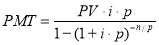Статья посвящена совершенствованию формул шести функций сложного процента, применяемых в теории и практики оценочной деятельности. Выявлены проблемы, связанные с реализацией общей базовой формулы сложного процента при внесении в нее размерности процентной ставки и числа периодов. Предложено внести в общую базовую формулу показателя «Периодичность начисления процентов» для модификации процентной ставки и числа периодов, чтобы в общей формуле сложного процента соблюдались правила математики. На основе модифицированной базовой формулы сложного процента представлены модифицированные формулы шести функций сложного процента. Приведена проверка правомерности модифицированных формул шести функций сложного процента на числовых примерах.
Ключевые слова :формулы сложного процента, процентная ставка, модифицированная процентная ставка, число периодов, правила математики, оценочная деятельность.
The article is devoted to the improvement of the formulas of six functions of a compound interest used in the theory and practice of appraisal activity. The problems associated with the implementation of the total basic formula of a compound interest were identified when introducing the percentage rate and the number of periods into it. It is proposed to introduce into the general basic formula the indicator “Frequency of interest” for modifying the interest rate and the number of periods, so that the rules of mathematics are observed in the general formula of a compound interest. Based on the modified basic formula of a compound interest, modified formulas of six functions of a complex percentage are presented. The legality of the modified formulas of six functions of a compound interest with numerical examples is checked.
Keywords: compound interest formulas, interest rate, modified interest rate, number of periods, math rules, valuation activities
В теории и практике оценочной деятельности широко применяются шесть функций сложного процента, из которых, в зарубежной литературе по оценочной деятельности, три функции являются базовыми, а три другие функции являются их обратными величинами.
В качестве примера в таблице 1 представлен состав и наименование шести функций сложного процента, употребляемый в зарубежной литературе по оценочной деятельности [1, c. 64].
Таблица 1
Базовые функции сложного процента и их обратные величины
|
Функции |
Обратные величины |
|
Накопленная сумма единицы (колонка 1) |
Текущая стоимость единицы (колонка 4) |
|
Накопление единицы за период (колонка 2) |
Фактор фонда возмещения (колонка 5) |
|
Текущая стоимость аннуитета (колонка 3) |
Взнос на амортизацию единицы (колонка 6) |
Следует отметить, что номера в колонках наименований функций указывают на последовательное расположение функций в стандартных таблицах расчета их величин. Иногда в теории и практике экономической деятельности такие номера используются в качестве упрощенного наименования функций сложного процента.
В отечественной литературе по оценочной деятельности шесть функций сложного процента состоят из трех функций наращения (накопления) и трех обратных им функций — функций дисконтирования [2]. Состав и содержание этих функций представлен в таблице 2.
Таблица 2
Функции наращения и дисконтирования сложного процента
|
Функции наращения |
Функции дисконтирования |
|
Накопленная сумма единицы (колонка 1) |
Текущая стоимость единицы (колонка 4) |
|
Накопление единицы за период (колонка 2) |
Текущая стоимость аннуитета (колонка 5) |
|
Фактор фонда возмещения (колонка 3) |
Взнос на амортизацию единицы (колонка 6) |
Все функции сложного процента имеют не только наименования, но и математические выражения, т. е. расчетные формулы, которые с принятыми в отечественной оценочной теории и практике обозначениями показателей в совокупности с их наименованиями составляют систему, состоящую их шести функций сложного процента (таблица 3).
Таблица 3.
Шесть функций сложного процента
|
Наименование функции |
Формула наращения (накопления) |
Наименование функции |
Формула дисконтирования |
|
Накопленная сумма единицы (будущая стоимость единицы) |
|
Текущая стоимость единицы |
|
|
Накопление единицы за период |
|
Текущая стоимость аннуитета |
|
|
Фактор фонда возмещения |
|
Взнос на амортизацию единицы |
|
В таблице 3 условные обозначения и расшифровки показателей взяты из работы [2]:

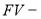
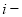
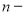

Все шесть функций сложного процента строятся с использованием общей базовой формулы
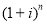
В финансовых расчетах величину
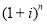
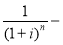
В общей базовой формуле сложного процента показатель
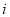
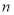
Процентная ставка является периодической, потому что проценты начисляются за определенный временной интервал, который называют периодом начисления. В качестве такого периода принимают год, полугодие, квартал, месяц или даже день [3, c. 17]. На практике чаще всего употребляются годовые (номинальные) процентные ставки (1/год), которые могут быть переведены в другие единицы измерения.
В литературе по финансовой математике приведены примеры перевода единицы измерения процентной ставки: «
Так, например, если дана годовая процентная ставка



Из приведенных суждений следует, что процентная ставка в общей базовой формуле сложного процента имеет как числовое значение, так и временную характеристику (год, квартал, месяц и т. д.).
Касательно показателя
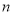
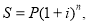
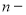
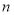
Следует отметить, что в приведенных в таблице 3 формулах накопления показатель
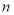
Если в основание

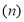
Следовательно, как показатель степени
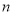
Для иллюстрации некорректности общей базовой формулы сложного процента рассмотрим ее содержание на числовых примерах.
Пример 1.
Пусть

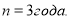
Подставим эти значения в общую базовую формулу сложного процента и получим выражение, не имеющее решения:
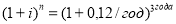
Если годовую процентную ставку и годовое число периодов последовательно переводить в полугодовые, ежеквартальные и ежемесячные единицы измерения, то получим следующие выражения общей базовой формулы сложного процента, не имеющие решения:
— при переводе годовой ставки в полугодовые единицы измерения:
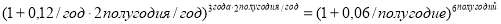
— при переводе годовой ставки в ежеквартальные единицы измерения:
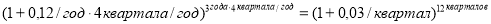
— при переводе годовой ставки в ежемесячные единицы измерения:
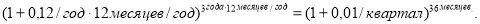
Приведенные выше числовые примеры перевода заданной годовой процентной ставки и заданного годового числа периодов в другие единицы измерения представляют собой более частое начисление процентов, чем раз в год. При этом новые единицы измерения процентной ставки и числа периодов сохраняются и не сокращаются.
В литературе по финансовой математике в случае более частого начисления процентов, чем раз в год, годовую процентную ставку преобразуют путем деления ее на число периодов начисления процентов в год и также преобразуют число периодов (срок инвестирования капитала) путем умножения его на период начисления процентов.
В результате такого преобразования (корректировки) годовая процентная ставка и число периодов превращаются в коэффициенты, не имеющие размерности, а формула в целом представляет собой эффективную процентную ставку за период накопления.
В таком случае общая формула сложного процента будет иметь следующий вид:
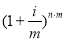
где
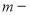
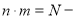
В формуле (1) показатель
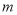
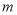
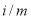

В качестве иллюстрации применения формулы (1) рассмотрим соблюдение правил математики при использовании исходных данных примера 1.
Пример 2.
Пусть

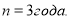
Подставим исходные данные в формулу (1) и получим следующие результаты:
— при годовом начислении процентов:
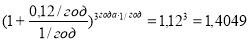
— при полугодовом начислении процентов:
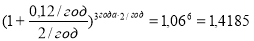
— при ежеквартальном начислении процентов:

— при ежемесячном начислении процентов:
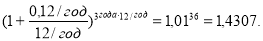
С математической точки зрения формула (1) является корректной, так как основание и показатель формулы (1) являются числовыми значениями, не имеющими размерности.
В литературе по оценочной деятельности в случае более частого начисления процентов (накопление короче года) в общую формулу сложного процента вносятся изменения: « При корректировке данной формулы число лет, на протяжении которых происходит накопление, умножается на его частоту в течение одного года; одновременно номинальная годовая ставка процента делится на частоту накопления. Результат покажет эффективную ставку процента за период накопления» [1, c. 39].
Из приведенной выше цитаты следует, что в случае начисления процентов короче года в оценочной деятельности применяется тот же метод, что и описанный выше.
Следует отметить, что недостатком общей формулы сложного процента, как основной, так и откорректированной, является отсутствие в ее составе в явном виде показателя «Периодичность начисления процентов», который является одним из ключевых показателей шести функций сложного процента.
Кроме того, при периодичности начисления процентов больше года формула (1) не имеет здравого смысла, так как частота начисления процентов в год будет меньше единицы.
При такой ситуации довольно сложно оперировать приведенными выше общими формулами сложного процента и в этой связи возникает необходимость изменить (модифицировать) основную общую базовую формулу сложного процента для соблюдения в ней правил математики, что и является целью настоящей работы.
Для достижения поставленной цели предлагается внести в общую базовую формулу сложного процента показатель «Периодичность начисления процентов» для корректировки номинальной годовой процентной ставки и числа периодов. В этом случае общая базовая формула сложного процента примет следующий вид:
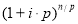
где
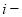
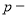

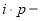

Теоретические обоснования целесообразности внесения в общую базовую формулу сложного процента показателя «периодичность начисления процентов» изложены в работах [5–7], поэтому этот вопрос в настоящей статье не рассматривается.
Рассмотрим расчет эффективной процентной ставки по формуле (2) на основе исходных данных примера 1.
Пример 3. Эффективная процентная ставка за период накопления капитала имеет следующие значения:
— при применении годовой процентной ставки:
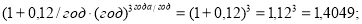
— при переводе годовой процентной ставки в полугодовые единицы измерения:
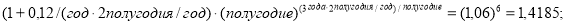
— при переводе годовой процентной ставки в ежеквартальные единицы измерения:
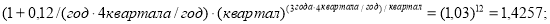
— при переводе годовой процентной ставки в ежемесячные единицы измерения:
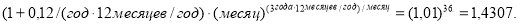
Откорректированная общая базовая формула (2) сложного процента является модифицированной формулой пригодной для любых значений периодичности начисления процентов и любых значениях числа периодов (сроках накопления капитала).
Если общий срок накопления капитала
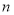
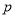
На основе модифицированной общей базовой формулы (2) в таблице 4 представлены модифицированные формулы шести функций сложного процента при платежах в начале каждого периода.
Таблица 4
Модифицированные формулы шести функций сложного процента
|
Наименование функции |
Формула |
|
|
модифицированная |
действующая [2, с. 11–22] |
|
|
1. Накопленная сумма единицы |
|
|
|
2. Накопление единицы за период |
|
|
|
3. Фактор фонда возмещения |
|
|
|
4. Текущая стоимость единицы |
|
|
|
5. Текущая стоимость аннуитета |
|
|
|
6. Взнос на амортизацию единицы |
|
|
Существенное различие между действующими и модифицированными формулами сложного процента заключается в том, что в модифицированных формулах сложного процента процентная ставка сопряжена с периодичностью начисления процентов, что приводит размерность этих показателей к безразмерной величине.
Кроме того, показатель
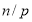
Для проверки правомерности модифицированных формул шести функций сложного процента рассмотрим их применение на конкретных примерах.
Пример 1. Исходные данные в случае применения 1-й формулы сложного процента:

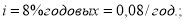
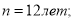
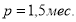
Определить значение
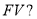
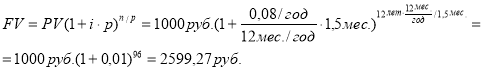
Пример 2. Исходные данные в случае применения 2-й функции сложного процента:

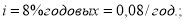
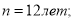
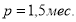
Определить значение
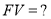

Пример 3. Исходные данные в случае применения 3-й функции сложного процента:
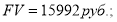
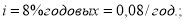
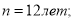
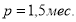
Определить значение
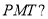
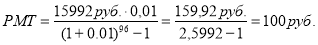
Пример 4. Исходные данные в случае применения 4-й функции сложного процента:
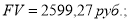
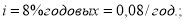
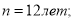
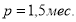
Определить значение
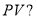
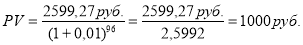
Пример 5. Исходные данные в случае применения 5-й функции сложного процента:
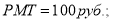
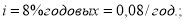
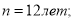
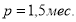
Определить значение
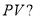
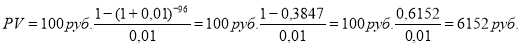
Пример 6. Исходные данные в случае применения 6-й функции сложного процента:
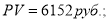
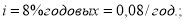
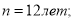
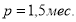
Определить значение
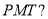
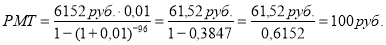
В приведенных выше шести примерах численные значения
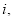
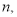

В таблице 4 формулы шести функций сложного процента могут применяться при различных сочетаниях значений показателей
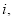
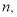
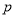
Выводы:
1. В учебной литературе по оценочной деятельности в общей базовой формуле сложного процента ставка процента и число периодов используются без указания единиц измерения, что является неправомерным.
2. При установлении единицы измерения процентной ставки и числа периодов нельзя по правилам математики в основании общей базовой формулы сложного процента суммировать единицу с процентной ставкой
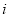
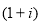
3. Для устранения недостатков в общей базовой формуле сложного процента предложено внести в нее показатель «Периодичность начисления процентов» для корректировки номинальной годовой процентной ставки и числа периодов, что позволяет применять общую базовую формулу (2) без нарушения правил математики. Общая базовая формула сложного процента в таком виде представляет собой модифицированную базовую формулу сложного процента.
4. На основе модифицированной базовой формулы сложного процента сформированы модифицированные формулы шести функций сложного процента, которые корректны с точки зрения применения правил математики.
5. Модифицированные формулы могут применяться при различных сочетаниях показателей
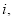
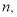
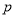
6. Статья может быть полезна слушателям системы повышения квалификации и профессиональной переподготовки оценщиков, практикующим оценщикам, преподавателям экономических вузов, предпринимателям, инвесторам, финансистам и иным лицам.
Литература:
- Фридман Дж., Ордуэй Ник. Анализ и оценка приносящей доход недвижимости. Пер. с англ., М.: «Дело Лтд», 1995. 480 с.
- Элементы финансовой математики для оценщиков (курс лекций и сборник задач). Составитель и ответственный редактор канд. физ.- мат. наук, зам.директора ПИНО Т.Г. Касьяненко. СПб., ЗАО «ПИНО», 1997. 64 с.
- Четыркин Е. М. Финансовая математика: Учебник. 4- е изд. М: Дело, 2004. 400 с.
- Бадюков В. Ф. Финансовая математика: учеб. пособие / В. Ф. Бадюков, М. Ю. Серкин. Хабаровск: РИЦ ХГАЭП, 2009. 92 с.
- Мочулаев В. Е. Уточненная формула сложных процентов и ее применение в теории оценки стоимости недвижимости // Конкурентоспособность в глобальном мире: экономика, наука, технологии. 2016. № 7. ч.1. С.242–245.
- Мочулаев В. Е. Методы накопления и дисконтирования денежных потоков в теории оценки стоимости предприятия (бизнеса) // Вопросы оценки, 2016. № 4. с.16–22.
- Мочулаев В. Е. Об учете размерности экономических показателей сложных процентов в оценочной деятельности // Молодой ученый. 2021. № 50. С.458–465.