В статье рассмотрено понятие «моделирование, представлена классификация видов моделирования, а также описаны сущность и применение математических и экономико-математических моделей, отмечены преимущества и недостатки экономико-математических моделей.
Ключевые слова: моделирование, экономико-математическое моделирование, планирование, прогнозирование, корреляционно-регрессионный метод, метод экспоненциального сглаживания, метод оптимизации, линейное программирование.
В настоящее время использование на практике формализованных моделей управления финансовыми показателями получает все большее распространение в ряде экономически развитых странах. Степень формализации находится в прямой зависимости от размеров организации: чем крупнее и известнее фирма, тем в большей степени ее руководство может и должно использовать формализованные подходы в финансовой политике.
Как пишет Каштаева С. В. [1] «моделирование можно рассматривать как замещение исследуемого объекта (оригинала) его условным образом, описанием или другим объектом, именуемым моделью и обеспечивающим близкое к оригиналу поведение в рамках некоторых допущений и приемлемых погрешностей. Моделирование обычно выполняется с целью познания свойств оригинала путем исследования его модели, а не самого объекта».
На рисунке 1 представлена классификация видов моделирования.
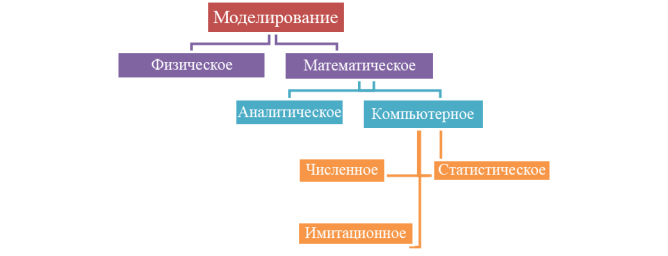
Рис. 1. Классификация видов моделирования
При физическом моделировании используется сама система или подобная ей система.
Математическое моделирование представляет собой процесс установления соответствия реальной системе математической модели и исследование этой модели для получения характеристики реальной системы.
Аналитическое моделирование — это запись процессов функционирования элементов модели в виде математических отношений (например, алгебраических, дифференциальных, логических).
При компьютерном моделировании модель формируется в виде алгоритма (например, программы для компьютеров), позволяя сделать над ней вычислительные операции.
Численное моделирование позволяет получить необходимые количественные данные о поведении систем или устройств каким-либо подходящим численным методом, таким как методы Эйлера или Рунге-Кутта.
Статистическое моделирование заключается в обработке данных о системе (модели) с целью получения статистических характеристик системы.
При имитационном моделировании происходит воспроизведение на компьютере того или иного процесса функционирования системы, которая взята для исследования, и соблюдается логическая и временная последовательность протекания процессов. Такое моделирование позволяет определить данные исследуемой системы в определенный отрезок времени.
Для того чтобы описать экономико-социальные системы и процессы используются экономико-математические методы, которые включают не только экономические дисциплины, но и математические.
По словам автора Каштаевой С. В. [1] «суть экономико-математического моделирования заключается в описании социально-экономических систем и процессов в виде экономико-математических моделей. Экономико-математические методы следует понимать как инструмент, а экономико-математические модели — как продукт процесса экономико-математического моделирования».
Основные задачи экономико-математического моделирования заключаются в следующем:
– анализ объектов, явлений и процессов, относящихся к экономике;
– экономическое прогнозирование, которое помогает предвидеть дальнейшее «поведение» тех или иных экономических явлений;
– принятие управленческих решений на основе прогнозных значений.
Экономико-математические методы планирования представляют собой приемы расчета экономических показателей с применением методов прикладной математики и математической статистики.
Как утверждает Моисеенко Ж. В. [4] «в современных условиях развитию моделирования и практическому применению моделей стала придаваться особая значимость в связи с усилением роли прогнозирования и переходом к индикативному планированию. С помощью экономико-математических методов появляется возможность всестороннего обоснования изменения экономических показателей».
Корреляционно-регрессионное прогнозирование широко распространено в области экономики и решает две основные задачи:
– устанавливает степень тесноты связи между планируемым (прогнозируемым) параметром и влияющими на него факторами;
– определяет с помощью уравнений регрессии форму связи между планируемым (прогнозируемым) параметром и влияющими на него факторами.
Вследствие того, что достичь идеальной модели невозможно, всегда приходится идти на определенные уступки, которые, как правило, относят к значимым недостаткам регрессионного анализа.
К таким недостаткам относятся:
– целенаправленный отказ от других факторов;
– невозможность определения и измерения определенных величин;
– агрегирование переменных;
– использование временной информации (при изменении временного интервала можно получить другие результаты регрессии);
– неверный выбор той или иной математической функции;
– недоучет в уравнении регрессии какого-либо существенного фактора, повлиявший на результат исследования;
– ошибки выборки;
– ошибки измерения.
Метод экспоненциального сглаживания. Одной из отличительных особенностей данного метода является то, что для определения сглаженного уровня в нем используются значения только предшествующих уровней ряда, умноженные на их веса.
Сглаженные значения временного ряда
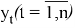
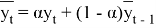
где
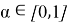
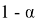
Преимущества данного метода заключаются в следующем:
– период изменения показателей — плавная линия (линия тренда);
– изменение объекта прогнозирования будет происходить так же, как в прошлом, настоящем и будущем;
– наличие достоверной статистической информации не менее чем за 4 года (временных периода);
– отсутствие форс-мажорных обстоятельств.
Недостатки метода экспоненциального сглаживания:
– ненадежность, если имеются значительные колебания в исторических данных;
– предположение, что прошлая тенденция будет продолжаться и в будущем, так как нужно учитывать также конкуренцию в бизнес-среде;
– игнорирование качественных факторов, таких как изменения вкусов и моды.
Метод оптимизации. К методу оптимизации относится метод линейного программирования, который является глубоко разработанным, наиболее эффективным, а также широко используемым на практике в экономической среде. Линейное программирование позволяет реализовать матричную модель планирования и прогнозирования.
Для построения матричной модели планирования и прогнозирования обычно вводят ограничения в виде аналитического и геометрического вида.
Задача линейного программирования заключается в оптимизационной задаче, в которой целевая функция линейна на множестве линейных ограничений (формула 2):
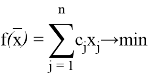
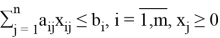
Ограничения, накладываемые на координаты
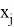
Преимуществами метода оптимизации являются:
– возможность использования с помощью ЭВМ;
– перебор вариантов позволяет найти оптимальное решение при заданных условиях.
Основной недостаток моделей оптимизации определяется самим построением моделей — форма записи в виде ограничений и целевой функции, что в большинстве случаев приводит к неадекватности построенной модели по отношению к реальной модели.
Таким образом, можно сделать вывод о том, что каждый из описанных в статье методов математического моделирования имеет как преимущества, так и недостатки, и нет единой рекомендации для применения того или иного метода. Выбор метода моделирования финансовой деятельности организации в большинстве случаев зависит от вида деятельности фирмы, ее прибыли, положения в экономической среде и от множества других факторов.
Литература:
1. Каштаева, С. В. Математическое моделирование: учебное пособие / С. В. Каштаева. — Пермь: ПГАТУ, 2020.
2. Костюченко, Т. Н. Прогнозирование и планирование социально-экономического развития: учебное пособие / Т. Н. Костюченко. — Ставрополь: СтГАУ, 2018.
3. Охотников, И. В. Прогнозирование и планирование: учебно-методическое пособие / И. В. Охотников, И. В. Сибирко. — Москва: РУТ (МИИТ), 2018.
4. Моисеенко, Ж. Н. Прогнозирование и планирование деятельности предприятия: учебное пособие / составитель Ж. Н. Моисеенко. — Персиановский: Донской ГАУ, 2019.







