This article discusses the systems of astronomical coordinates, the name of the stars, their position in the celestial sphere and the solution of various astronomical problems to determine the coordinates of various star systems.
Keywords: space bodies, sky, radius, celestial sphere, zenith, horizon, equator, meridian, horizontal coordinates, equatorial coordinates.
- Introduction
A stronomical coordinates. Coordinates are numbers that determine the position of a point. Thus, for example, geographic latitude and longitude are called geographic coordinates, since they express the position of a point on the earth's surface by means of them. There are several systems of astronomical coordinates, with the help of which the position of points on the celestial sphere is determined. These systems differ from one another in the choice of the main plane and the beginning of the count. In each such system there are always two coordinates, one of which is quite similar to the earth's latitude, the other to longitude. In some problems it is more convenient to use one coordinate system, and in others — another.
Astronomy provides information about the structure and evolution of the universe based on the study of the structure, motion and position of cosmic bodies, and teaches mathematical methods for determining the apparent position of lights in the sky, the theory of finding the exact time, observations. To determine the visible position of lights at any time, it is necessary to know their laws of visible motion.
To study the visible conditions and movements of celestial bodies, it will be necessary to determine their position during observation. To do this, it is sufficient to study the celestial position of the stars in relation to certain directions, and in most cases there is no need to determine the distances to them. Before studying the visual states and movements of lights, it is necessary to become acquainted with the main points, lines, and circles of the sky. A celestial sphere is a sphere whose radius is arbitrarily taken and whose center lies in the eye of the observer, in which the stars are projected in the same way as the stars appear in the sky at a given time. One of the two points of the vertical line passing through the observer at the center of the celestial sphere, which intersects with the celestial sphere, is called the zenith (Z '), and the other, which lies diametrically opposite to it, is called the nadir (Z').
The straight line connecting these points of the sphere is called the vertical line. A large circle formed by the intersection of a celestial sphere with a plane perpendicular to a vertical line from its center is called a mathematical horizon. The large circles formed by the intersection of the sphere with the planes passing through the vertical axis are called vertical circles. The points and lines mentioned above vary depending on the observer's position on the Earth's surface. The celestial sphere has points and lines connected to the main lines and points of the globe that do not change their state even when observed from anywhere on Earth.
The visible motion of celestial bodies is a visual phenomenon that reflects the Earth's own axis and its rotation around the Sun. Therefore, methods are used to find the position of celestial bodies depending on the motion of the Earth [1,13].
- Methods
1 — method. The North Star is the brightest star in the constellation Ursa Major. As we have previously determined, the latitude of a given place is equal to the height (hp) of the Universe pole above the horizon at that point, i.e. = hp. Therefore, it can be concluded that the height of the World Pole in Tashkent is about 41020 ', and the latitude of Tashkent is 41020'.
In other words, if it is necessary to approximate the latitude of a particular location on the Earth, it is sufficient to measure the height of the Universe from the horizon.
2
— method.
It is possible to directly measure the height h
0
of the Sun at noon in a given settlement and to find the latitude of the place according to the
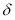
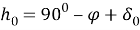
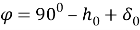
The numerical values that determine the position of a point in the celestial sphere are called astronomical coordinates. In astronomy, several astronomical coordinate systems are used. These systems differ from each other in the choice of the main planes used in them and the beginning of the calculations. Depending on the solution of the problem, a certain astronomical coordinate system is used [10, 13].
Horizontal coordinates . If we take the plane of the horizon as the principal plane, then the zenith will be the principal point. We pass a large circle through the zenith and σ star. All large circles passing through the zenith are perpendicular to the horizon, and they are called vertical circles or verticals. The coordinates of this system are: altitude h and azumite A.
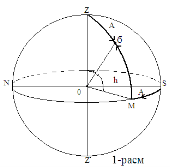
Fig. 1

To find the height, we draw a large circle passing through the zenith and the σ star whose height must be found. Along this circle, the arc M σ transferred from the horizon to σ is the height h. Its central angle is MO σ (Fig. 1).
From the horizon to the zenith h is positive and to the south it is negative.
At the zenith, the height of the star is h = 90
0
, nadir h = -90
0
, and on the horizon h = 0
0
. Sometimes the zenith distance of the star is used instead of the height z — the angular distance of the star from the zenith. The distance from the zenith is calculated from 0
0
to 180
0
, and the altitude from 0
0
to ± 90
0
. Obviously, h + z =
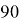
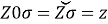
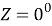
The angle formed at the zenith between the vertical of the lamp and the meridian is azimuth (A). From Figure 1
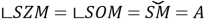
The horizontal coordinate system is widely used in determining geodetic, topographic, geographical coordinates. When horizontal coordinates are given, their measured time must also be given. The altitude (h) and azimuth (A) vary in diurnal motion because the diurnal line of the stars along the celestial sphere is parallel to the equator, and h and A are taken relative to the motionless observer and its horizon. The horizon with the equator is generally angular. The poles of the sky fall on the horizon only where they appear to be at the zenith, that is, at the poles of the Earth [1, 3, 8].
III. Strengtheni ng
Issue 1. σ is the height of the star h = 30 0 , azimuth A = 280 0 ; find its place in the celestial sphere.
We will use Figure 2 to solve the problem. In the celestial sphere, we define the direction to the main plane — the horizon and the zenith, the north and south points. To find the position of the star, we draw an arc from the south point (S) in the clockwise direction A = 280 0 . It comes to point M. An altitude circle must pass through point M.
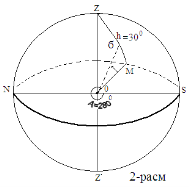
Fig. 2
If we draw an arc h = 30 0 towards this zenith in this circle, we will find the position of the star σ. The σ star is on the southeast side of the celestial sphere.
The first system of equatorial coordinates. The main plane is the equatorial plane. The position of the star is determined by the angle of inclination δ and the angle of the clock (t) (Fig. 3).
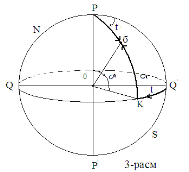
Fig. 3
The large circle passing through the σ star and the pole is called the deflection circle. To find the
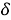
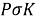
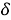
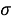
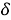
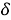
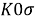
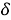

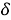
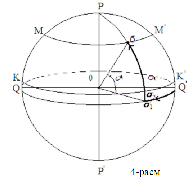
Fig. 4
Due to the diurnal rotation, the clock angle t changes in the equatorial coordinate system. The difference between such changes and the azimuth A change is that the clock angle changes in proportion to time t. The clock angle varies from 0 0 to 360 0 on a flat surface during the day. It is therefore very convenient to express the angles of the clock in the hour scale, since the amount of change in the angles of the clock is equal to the time taken for this change. Based on this, you can create the following table: 24 hours → 360 0 1 hour → 15 0 , 1 minute → 15 ', 1 0 → 4 minutes, 1 second → 15``, 1` → 4 seconds. The hour is denoted by h, the minute by m, the second by s. For example, 37 0 5` = 2h 30m, ie 2 hours 30 min; 7h20m = 110 0 . These writings are very useful in the transition from the measurement of degrees to units of time and vice versa, from the measurement of units of time to the measurement of degrees.
Because the clock angle t fluctuates during the day, it is not used to create star maps and catalogs, such as equatorial coordinates. A second system of equatorial coordinates is introduced to create star maps and catalogs [3, 10].
Issue 2. t 1 = 3h21m; t 2 = 9h26m in degrees and t 3 = 17 0 57`1``; Express t 4 = 17 0 13`59`` in hours.
Answer: t 1 = 50 0 15`; t 2 = 141 0 30`; t 3 = 1h11m48,06s; t 4 = 12h44m55,9s;.
The second system of equatorial coordinates. In solving many astronomical problems, it is necessary to use a system in which both coordinates do not change. For this purpose, another variable is obtained in place of the variable t in the first system of equatorial coordinates. Since it is convenient to express the second coordinate with the arc of the equator, it is necessary to choose a point of the celestial equator as the starting point of the calculation; the most convenient point for this is the point of spring equinox, i.e. the point where the equator intersects the Sun on March 21 from the southern hemisphere of the sky to the northern hemisphere. This point is indicated by the symbol γ (not the letter). This point, like all points of the equator, participates in the diurnal motion of the sky. When the sun reaches this point in its annual motion, the length of day and night are equal throughout the Earth (Figure 5) [3, 2, 9].
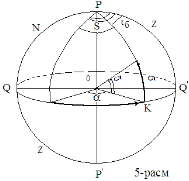
Fig. 5
The first coordinate of the equatorial coordinate system remains the deviation
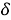
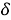
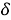
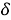
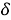
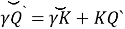
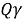
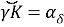
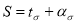
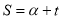
If t is known in the following equation, it is possible to find
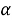
Issue 3. In the second system of equatorial coordinates, the coordinates of the stars are:
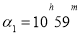
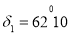
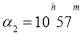
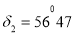
Using a star map, say the names of these stars and determine their position in the sky.
At the end of the astronomy textbook for secondary schools and universities, a sliding map of the starry sky is given. On this map, the celestial equator and parallels are marked by concentric circles, and the deflection circles are marked by straight lines drawn in different directions from the pole. The correct output α is expressed in units of time converted externally; the deviations are expressed in degrees, on the line of deviation passing through the point of spring equinox. From the outer circle on the star map we find the point
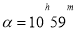
IV. Discussion
Astronomical observation at school aims, firstly, to acquaint students directly with those celestial phenomena, acquaintance with which is absolutely necessary for the presentation of astronomy. These kinds of observations are so important that, in the absence of them, it is impossible to present astronomy with confidence that the students have understood it properly.
In addition to this main goal, astronomical observations also have a second goal — to give students elementary practice in applying the knowledge they gain to carrying out such work, which is used on a large scale in the national economy and in ordinary everyday practice. Observational work of this kind will be referred to below as practical work. Practical work is also important because it provides material for testing the knowledge that students have.
We can divide observations of the first kind into two groups: 1) introductory — giving students direct knowledge of the phenomenon itself in order to lead them to generalizations and conclusions in the classroom, and 2) illustrative — aimed at supplementing the presentation of an already known object with a more detailed study of it. These names indicate the main purpose of such practical work: observations of the first kind, generally speaking, precede the passage of a certain section of the course, observations of the second kind are carried out after the student has studied the same section of the course.
It is quite obvious that illustrative observations can, and in some cases must have the same object with introductory ones. Introductory observations should be made in relation to all sections of the course, but especially to the section of spherical astronomy and elements of theoretical astronomy.
References:
- И. Ф. Полак. Умумий астрономия курси. Т., «Ўқитувчи» 1965.
- Е. П. Левитан. Астрономия. Книга для учителя. 11 класс. Москва «Просвещение» 2011.
- Г. Мурсалимова., А. Рахимов. Умумий астрономия курси. Т., «Ўқитувчи» 1976.
- В. Н. Глазков. Астрономия. Москва 2015
- Берененко, Т.С., Кругликов, В. В. Наблюдаемые характеристики небесных тел: Учебное — методическое пособие / Т. С. Берененко, В. В. Кругликов; МОРФ. — Томск: УМПЦ ППУ, 2000.
- Бакулин Г. Н., Еононович Э. В., Морозов В. И. Курс общей астрономии. М., «Наука», 1993.
- М. Мамадазимов. Астрономия. Т., «Ўқитувчи» 2003.
- Клищенко А. П., Шупляк В. И. Астрономия. — М., «Новое знание», 2004.
- Кононович Э. В., Мороз В. И. Общей курс астрономии, М., «УРСС», 2004.
- Нуритдинов С.Н, Гайнуллина Э. Р. Общая астрономия: задачи и упражнения, Т.: НУУз, 2006
- Karttunen H. et al. Fundamental Astronomy. Springer, 2007, ISBN-13: 978–3540341437
- Кононович Э. В. Общий курс астрономии: Учебное пособие для вузов / Э. В. Кононович, В. И. Мороз; под ред. В. В. Иванова. — М: УРСС, 2011.
- М.Мамадазимов. Астрономия. O’rta ta’lim muassasalarining 11 — sinfi o’rta maxsus, kasb — hunar ta’limi muassasalarining o’quvchilari uchun darslik. T., «Davr nashriyoti» 2018.
- Dehqonova, O. Role of math knowledge in the process of laboratory works in physics.
- Dehqonova, O. Q. (2020). Connectivity evaluation of physics and mathematics in secondary schools. Scientific reports of Bukhara State University, 4(3), 307–311.
- Dehqonova, O., Urazov, A., & Mamatmuradova, M. (2021). On the connectivity of physics and mathematics in high school education. Физико-технологического образование, 6(6).
- Qosimjonovna, D. O. (2021). Use of ict tools to increase the effectiveness of teaching physics in general secondary SCHOOLS. Berlin Studies Transnational Journal of Science and Humanities, 1(1.5 Pedagogical sciences).
- Dehqonova, O., & Taylanov, N. (2022). Extracurricular activities and their types in high schools. Физико-технологического образование, (2).
- Dehqonova, O., & Taylanov, N. (2022). The application of electronic multimedia resources for students in physics learning. Физико-технологического образование, (2).







