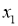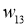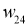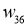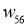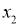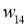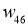В статье приводится обзор алгоритма обучения на основе обратного распространение ошибки. В результате были оценены параметры нейронной сети с применением алгоритма обратного распространение ошибки. Полученные результаты являются примером работы искусственной нейронной сети, обеспечивающих процесс распознавания или классификация образов без переобучения.
Ключевые слова: глубокие нейронные сети, нейронные сети, метод обратного распространения ошибки.
Введение. Глубокие нейронные сети содержат множество нелинейных скрытых слоев, что делает их очень эффективными моделями, которые могут выявить очень сложные взаимосвязи между их входами и выходами. Однако, при ограниченных обучающих данных многие из этих сложных взаимосвязей будут результатом шума выборки, поэтому они будут существовать в обучающем наборе, но не в реальных тестовых данных, даже если они взяты из того же распределения. Это приводит к переоснащению, а для его уменьшения было разработано множество методов. Они включают в себя прекращение тренировки, как только производительность на проверочном наборе начинает ухудшаться, введение различных штрафов за вес, таких как мягкое распределение веса по Новлану и Хинтону [1].
Алгоритм обратного распространения ошибки применяется для многослойного перцептрона [2]. У ИНС имеется входы


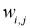

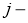


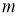
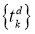


Для модификации весов будем реализовывать метод стохастического градиентного спуска, то есть будем подправлять веса после каждого тестового примера. Нам нужно двигаться в сторону, противоположную градиенту, то есть добавлять к каждому весу

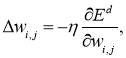
где

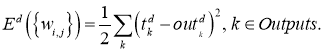
Производная считается следующим образом. Пусть сначала
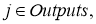
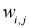
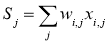
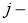

Аналогично,
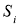
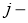
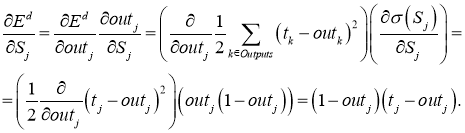
где

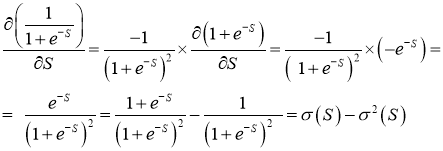
Если же


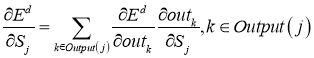
и
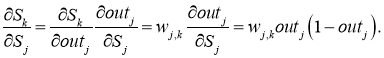
Причём


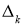
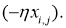
— для узла последнего уровня
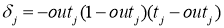
— для внутреннего узла сети
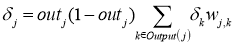
— для всех узлов

Получающийся алгоритм представлен ниже. На вход алгоритму, кроме указанных параметров, нужно также подавать в каком-нибудь формате структуру сети. На практике очень хорошие результаты показывают сети достаточно простой структуры, состоящие из двух уровней нейронов — скрытого уровня (hidden units) и нейронов-выходов (output units); каждый вход сети соединен со всеми скрытыми нейронами, а результат работы каждого скрытого нейрона подается на вход каждому из нейронов-выходов [3]. В таком случае достаточно подавать на вход количество нейронов скрытого уровня.
Алгоритм:
BackPropagation
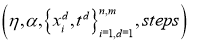
-
Инициализировать

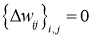
-
Повторить

Для всех d от 1 до m:
a) Подать
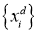
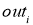
b) Для всех


c) Для каждого уровня
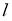
Для каждого узла

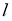
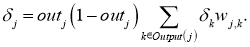
Для каждого ребра сети


-
Выдать значения
Примеры и эксперименты. Чтобы продемонстрировать, как эта теория выглядит на практике, приведём расчёты, демонстрирующею обратного распространения ошибки в простой нейронной сети с тремя слоями: входными, скрытыми и выходными (рис. 1). Стоит отметить, что ИНС обучаются посредством уточнение весовых коэффициентов своих связей. Этот процесс управляется ошибкой — разностью между правильным ответом, и представляемыми тренировочными данными, и фактически выходными значениями ошибка на выходных узлах определяются простой разностью между желаемыми и фактическими выходными значениями.
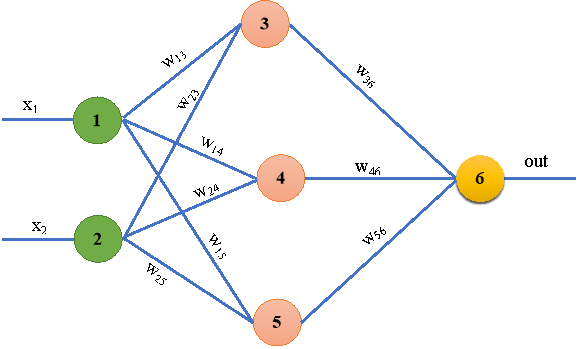
Рис 1: Стандартной ИНС
Таблица 1
Предварительное значение для параметров ИНС
|
|
1 |
|
1 |
|
-3 |
|
2 |
|
0,3 |
|
0,3 |
|
|
2 |
|
-1 |
|
3 |
|
-2 |
|
0,4 |
|
0,5 |
Приведенная выше картинка с тремя слоями нейронов, каждый из которых связан с каждым из нейронов в предыдущем и следующем слоях, выглядит следующим образом. Однако очевидно, что рассчитать распространение входных сигналов по всем слоям, пока они не превратятся в выходные сигналы, весьма непросто. Здесь покажем, как работает этот механизм, чтобы можно было представить, что происходит в ИНС в действительности, даже если впоследствии будет использован компьютер, для реализации алгоритма. Поэтому попытаемся проделать необходимые вычисления на примере меньшей нейронной сети, состоящей всего лишь из одного скрытого слоя, который включает в себя 3 нейрона, как показано выше.
Первоначально вычислим значение нейронов скрытого слоя:
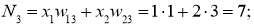
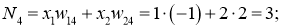

Далее для каждого нейрона применяем функцию, которая получает входной сигнал, но генерирует выходной сигнал с учётом порогового значения. В данном случае применяем функцию активацию RelU.

Исходя из этого, вычислим взвешенное значение:
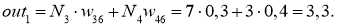
Так как на выходе ожидался результат


Продвигаясь в обратном направление от последнего входного слоя, нетрудно видить, как информация об ошибке в выходном слое используется для определения величины поправок к весовым коэффициентам связей, со стороны которых к нему поступают сигналы. Здесь используется общее значение
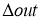

Далее эту ошибку умножим на веса активных нейронов:
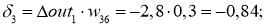
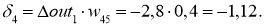
Для вычисления дельта весов необходимо оценить скорость обучение нейронной сети (Neural network learning rate (LR)): для нашего примера возьмём
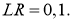
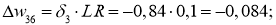
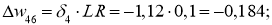
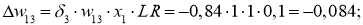

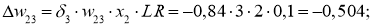
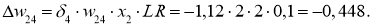
Ошибка ИНС является функцией весов внутренних связей. Улучшение нейронной сети означает уменьшение этой ошибки посредством изменение указанных весов. Далее производим обновление весов активных нейронов:
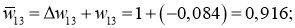
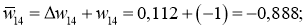

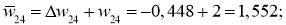
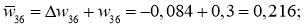
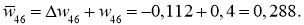
После обновление всех весов вычисляем заново все нейроны и выход.
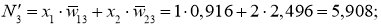
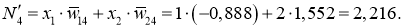
Далее для каждого нейрона применяем функцию RelU:
Исходя из этого, вычисляем взвешенное значение:
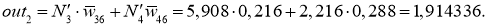
Так как не был достигнут желаемый результат (

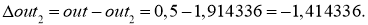
Эту ошибку умножаем на веса активных нейронов:
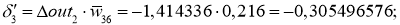
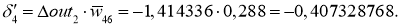
Далее для вычисления дельта весов нам необходимо определить скорость обучение нейронной сети (Neural network learning rate (
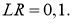
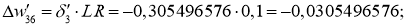
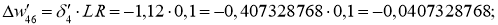

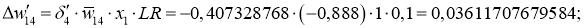


Далее производим обновление весов активных нейронов:
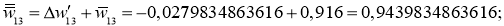


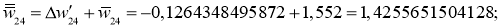
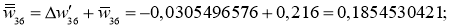
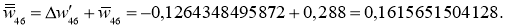
После второго обновления всех весов вычисляем заново все нейроны и выход:
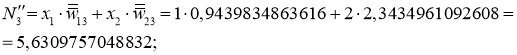
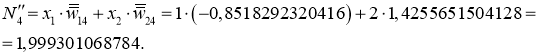
Наконец вычисляем взвешенное значение:

Вывод. Итак, так как ещё не достигнут желаемый результат (
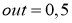
Литература:
- Nowlan. S. J. and Hinton, G. E. Simplifying neural networks by soft weight sharing.Neural Computation, 4, 173–193.
- Горбань А. Н., Россиев Д. А., Нейронные сети на персональном компьютере. — Новосибирск: Наука, 1996. — 276 с.
- Хайкин С. Нейронные сети. Полный курс — М.: «Вильямс», 2006. — 1104 с.