В статье рассматривается понятие модуля числа в курсе школьной математики. Показана важность данной темы для учащихся и применение. В программе школьного курса математики не имеется систематизация и обобщение знаний о модулях, об их свойствах, которые получают учащиеся за весь период обучения. Данный пробел и рассматривается в настоящей статье.
Ключевые слова: модуль числа, уравнения и неравенства, содержащие знак модуля, абсолютная величина.
Одной из сложных тем по математике для учеников 6 класса является тема «Модуль числа», для учеников старших классов «Уравнения и неравенства, содержащие знак модуля». Задача учителя доступными методами преподнести теоретический материал о модуле числа, о решении уравнений и неравенств, содержащих знак модуля, и через решение задач закрепить новые знания по изучаемой теме. В данной статье рассматривается преемственность понятия модуля числа, модуля алгебраических выражений, уравнения и неравенства с модулем.
Основная часть
Слово «модуль»- образовалось от латинского слова modulus, что в означает в переводе «мера». Считается, что Роджер Котс, английский математик и философ, который являлся в свою очередь учеником известного ученого Исаака Ньютона, использовал этот термин впервые. Исходя из иной версии термин «модуль» в 1806 году ввел Жорж Аргон, французский математик. Известный немецкий физик, математик, философ и изобретатель Готфрид Лейбниц использовал в своих трудах и работах функцию модуля. Но все же, современное и общепринятое утверждение модуля как абсолютной величины дал в 1841 году немецкий математик Карл Вейерштрасс.
Абсолютная величина или же модуль числа x — это неотрицательное число, которое, выражаясь неформальным языком, обозначает расстояние между началом координат и x. Модуль — одна из важных характеристик числа области действительных и комплексных чисел. В разделах школьного курса математики и высшей математики понятие модуля используется очень часто и поэтому оно занимает важное место в формировании математического аппарата школьника. Понятие «модуль» вводится в курс школьной математики 6 класса, используя его в геометрическом смысле, при этом модуль применяется не как унитарная операция, а именно на множестве чисел. Кроме того, в 6 классе математики модуль используется при делении и умножении отрицательных и положительных чисел, при сравнении чисел, а также рассматриваются несколько простейших неравенств и уравнений с использованием модуля. В курсе школьной геометрии изучаются понятия вектора и его длины, которая вычисляется с помощью модуля. В старших классах рассматриваются повторные понятия модуля числа и модуля выражения, решаются простейшие задачи с модулем, к примеру, линейные уравнения и неравенства с модулем. Задания, связанные с модулем, очень часто применяются на математических олимпиадах и на Едином Национальном Тестировании. В математическом анализе термин модуль используется в определениях основных понятий, таких как ограниченная функция, предел, производная и др. В настоящее время, понятие функции модуля, внесли в список функций практически всех стандартных языков программирования, так как данная функция проста в вычислении.
При объяснении ученикам 6 класса темы «Модуль числа» целесообразно рассмотреть следующие задачи:
Пример 1. Найдите модуль положительного числа 5.
Решение: Число 5>0. Отметим на координатной прямой точку А(5) (Рис.1).
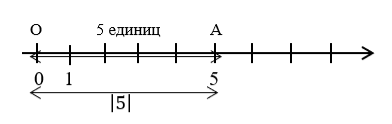
Рис. 1
Расстояние от начальной точки отсчета до точки А(5) равно 5 единичным отрезкам. Тогда, модуль числа 5 равен 5.
Пишут:
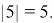
Читают: модуль числа 5 равен 5.
Пример 2. Найти модуль отрицательного числа 3.
Для того, чтобы найти модуль числа -3, на координатной прямой следует отметить точку B(-3) (Рис.2) .
Расстояние от начальной точки отсчета до точки В(–3) равно 3 единичным отрезкам. Из этого следует, что модуль числа –3 равен 3.
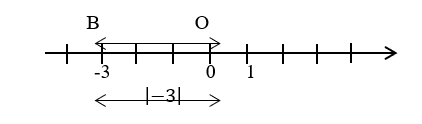
Рис. 2
При объяснении темы «Уравнения и неравенства, содержащие знак модуля» для старших классов целесообразно рассмотреть следующие примеры:
Пример 3. Решите уравнение:
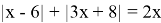
Решение: Так как,
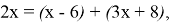
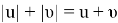
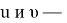
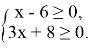
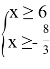
Значит,
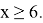
Ответ:
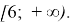
Пример 4. Решите неравенство:
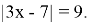
Решение: Применяя геометрический смысл модуля, получаем, что заданное неравенство равносильно неравенству
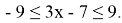
Таким образом,
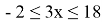
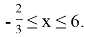
Ответ:
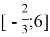
Заключение
Предложенные задачи будут способствовать глубокому усвоению нового материала и в дальнейшем ученики не будут испытывать трудности при решении задач данного типа.
Литература:
1. Марш М. Я. Выгодский «Справочник по элементарной математики», 2006.
2. Азаров А. И., «Математика для старшеклассников: Методы решения алгебраических уравнений, неравенств и систем: Пособие для учащихся учреждений, обеспечивающих получение общего среднего образования», 2004.
3. https://ru.wikipedia.org/wiki/Абсолютная_величина.
4. Веременюк В. В., «Математика: учимся быстро решать тесты: пособие для подготовки к тестированию и экзамену»,2006.







