В статье приводится обзор метода dropout оптимизации нейронных сетях, который сделал возможным широкое практическое применение данной технологии.
Ключевые слова: глубокие нейронные сети, dropout.
Введение. Глубокие нейронные сети содержат множество нелинейных скрытых слоев, что делает их очень эффективными моделями, которые могут выявить сложные взаимосвязи между входами и выходами.
При неограниченных вычислениях лучший способ “упорядочить” модель фиксированного размера — это усреднить прогнозы всех возможных настроек параметров, взвешивая каждую настройку по ее апостериорной вероятности с учетом обучающих данных. Иногда это может быть довольно хорошо аппроксимировано для простых или небольших моделей (см. [1]). (Салахутдинов и Мних, 2008). Однако, целесообразнее приблизиться к производительности золотого стандарта Байеса, используя значительно меньше вычислений. В этой связи предлагается сделать это путем аппроксимации одинаково взвешенного среднего геометрического значения предсказаний экспоненциального числа изученных моделей, которые имеют общие параметры.
|
|
|
|
|
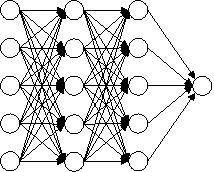
(a) Стандартная искусственная нейронная сеть (ИНС) |
b) ИНС после применения процедуры dropout |
Рис. 1: Модель искусственной нейронной сети отсева (dropout). Слева: Стандартная нейронная сеть с 2 скрытыми слоями. Справа: Пример утонченной сети, созданной путем применения процедуры отсева dropout к сети исходной ИНС зачеркнутые части были отброшены
Комбинация моделей почти всегда повышает производительность методов машинного обучения. Однако в случае больших ИНС очевидная идея усреднения результатов многих отдельно обученных сетей является непомерно дорогой. Объединение нескольких моделей наиболее полезно, когда отдельные модели отличаются друг от друга, но для того, чтобы модели нейронных сетей отличались друг от друга, они должны либо иметь разную архитектуру, либо обучаться на разных данных. Обучение множеству различных архитектур затруднено, потому что поиск оптимальных гиперпараметров для каждой архитектуры является сложной задачей, а обучение каждой большой сети требует больших вычислений. Более того, большие ИНС обычно требуют больших объемов обучающих данных, но может быть недостаточно доступных данных для обучения разных сетей на разных подмножествах данных. Даже если бы удалось обучить множество различных крупных сетей, использование их всех во время тестирования невозможно в приложениях, где важно быстро реагировать.
Метод отсева или Dropout — это метод, который решает обе эти проблемы. Его предназначение — предотвращение переобучения и обеспечение способа приблизительного эффективного объединения экспоненциально большого количества различных архитектур нейронных сетей. Термином “dropout” обозначается отсевающие единицы (скрытые и видимые) в нейронной сети. Под удалением блока подразумевается временное удаление его из ИНС вместе со всеми входящими и исходящими подключениями, как это показано на рис. 1. Выбор того, какие блоки будут отключаться, является случайным. В простейшем случае каждый узел (единица) сохраняется с фиксированной вероятностью
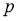
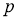
|
|
|
|
|
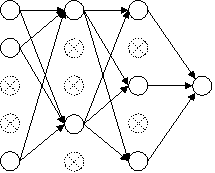
(a) Во время обучения |
(b) Во время тестирования |
Рис. 2. Слева: Узел вычисления во время обучения, который присутствует с вероятностью
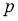
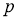
Применение dropout к ИНС равносильно выборке из нее “разреженной” сети. Разреженная сеть состоит из всех подразделений, которые пережили отсев (рис. 1b). Нейронную сеть с
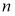
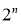
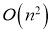
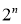
Во время тестирования невозможно явно усреднить прогнозы из экспоненциально большого числа уменьшенных моделей. Однако очень простой метод приблизительного усреднения хорошо работает на практике. Идея состоит в том, чтобы использовать единую ИНС во время тестирования без отсева. Веса этой сети являются уменьшенными версиями обученных весов. Если узел сохраняется с вероятностью
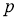
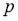
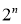
Идея “dropout” не ограничивается только ИНС с прямой связью. Она может быть более широко применена к графическим моделям, таким как машины Больцмана.
Описание модели.
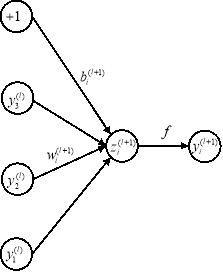
Рассмотрим модель ИНС с dropout (отсевам). Пусть ИНС имеет
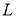
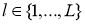
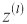
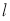
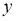
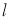
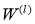
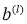
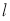
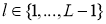
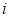
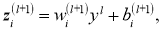
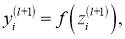
где
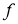
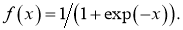
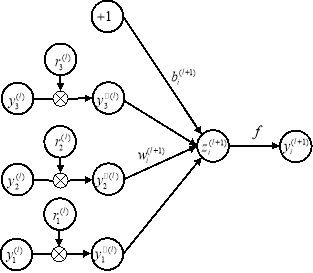
При выполнении процедуры dropout уравнение (1) модифицируется следующим образом (рис. 3b):
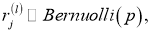
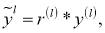
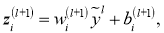

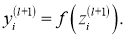
|
|
|
|
(a) Стандартная сеть |
(b) Сеть dropout |
Рис. 3: Сравнение основных действий стандартной ИНС и ИНС, регулируемой посредством dropout
Здесь
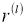
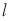
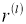
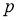
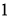
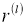
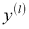
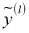
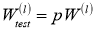
Обучающиеся ИНС с отсевом (dropout). Нейронные dropout сети могут быть обучены с использованием стохастического градиентного спуска способом, аналогичным стандартным ИНС. Единственное отличие состоит в том, что для каждого обучающего эпизода в мини-пакете выбираем уменьшенную сеть, отбрасывая узлы (блоки). Прямое и обратное распространение для этого обучающего примера выполняется только в этой уменьшенной сети. Градиенты для каждого параметра усредняются по обучающим наборам в каждой мини-партии. Любой тренировочный случай, в котором не используется параметр, вносит нулевой градиент для этого параметра. Для совершенствования стохастического градиентного спуска было использовано множество методов, таких как скорость обучения с отжигом и снижение веса [6]. Было выявлено, что они также полезны для ИНС dropout [7].
Одна конкретная форма регуляризации оказалась особенно полезной для dropout— ограничение нормы входящего вектора веса в каждой скрытой части, которая должна быть ограничена сверху фиксированной константой
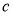
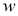
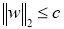
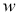
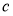
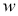
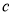
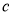
Хотя dropout сам по себе дает значительные улучшения, использование dropout наряду с регуляризацией максимальной нормы, высокой скоростью обучения и высокой динамикой обеспечивает значительный прирост по сравнению с простым использованием dropout. Возможное обоснование состоит в том, что ограничение векторов веса, лежащих внутри сферы фиксированного радиуса, позволяет использовать огромную скорость обучения без возможности увеличения веса. Шум, создаваемый dropout, затем позволяет процессу оптимизации исследовать различные области весового пространства, которые в противном случае были бы труднодоступны. По мере снижения скорости обучения оптимизация выполняется более короткими шагами, тем самым проводя меньше исследований, и в конечном итоге сводится к минимуму.
Сети dropout перед обучением. Нейронные сети могут быть предварительно обучены с использованием стеков RBM [8] (Хинтон и Салахутдинов, 2006), автокодеров (Винсент и др., 2010) или глубоких машин Больцмана [9] (Салахутдинов и Хинтон, 2009). Предварительная подготовка — это эффективный способ использования немаркированных данных. Было показано, что предварительная подготовка с последующей точной настройкой с обратным распространением в некоторых случаях значительно повышает производительность по сравнению с точной настройкой при случайных инициализациях.
Dropout может быть применен для точной настройки сетей, которые были предварительно обучены с использованием этих методов. Процедура предварительной подготовки остается прежней. Веса, полученные в результате предварительной тренировки, должны быть увеличены в
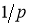
Реализация метода dropout и примеры
Основным фактором снижения вычислительной нагрузки на аппаратное обеспечение является снижение количества как самих нейронов, так и количества связей между ними — синапсов. При этом важной является задача определения незначимых синапсов и нейронов. При классической реализации алгоритма обратного распространения ошибки отсутствие корреляции между какими-либо входными параметрами может внести излишние шумы в выходной результат.
Метод Dropout с заданной вероятностью выключает некоторые нейроны, что в результате упрощает структуру сети. Посредством такого прореживания получают набор нейросетей и проводят их обучение на одинаковом обучающем наборе. Полученные веса синапсов затем усредняются в исходной структуре нейросети. Данный метод предотвращает совместную адаптацию между скрытых слоёв, которая приводит к переобучению сети.
Рис. 4. Пример работы метода Dropout
Вывод. Dropout — это метод улучшения нейронных сетей за счет сокращения переобучения. Стандартное обучение с обратным распространением создает хрупкие, которые работают с обучающими данными, но не обобщаются на невидимые данные. Случайный dropout разрушает эти коадаптации, делая ненадежным присутствие какого-либо конкретного скрытого подразделения. Было обнаружено, что этот метод улучшает производительность ИНС в широком спектре областей применения, включая классификацию объектов, распознавание цифр, распознавание речи, классификацию документов и анализ данных вычислительной биологии. Это говорит о том, что dropout является общим методом и не является специфичным для какой-либо области. Методы, использующие dropout, достигают самых современных результатов в SVHN, ImageNet, CIFAR100 и MNIST. Dropout значительно улучшил производительность стандартных нейронных сетей и на других наборах данных [10].
Одним из недостатков dropout является то, что он увеличивает время обучения. Обучение сети dropout обычно занимает в 2–3 раза больше времени, чем у стандартной ИНС той же архитектуры. Основной причиной этого увеличения является то, что обновления параметров является зашумленным. Каждый обучающий пример эффективно пытается обучить другую случайную архитектуру. Следовательно, вычисляемые градиенты не являются градиентами окончательной архитектуры, которые будут использоваться во время тестирования. В этой связи неудивительно, что обучение занимает много времени. Однако вполне вероятно, что эта стохастичность предотвращает переобучение. Это создает компромисс между переобучением и временем обучения. При большем времени обучения можно использовать высокий dropout, чтобы меньше страдать от переобучения.
Литература:
- R. Salakhutdinov and A. Mnih. Bayesian probabilistic matrix factorization using Markov chain Monte Carlo. In Proceedings of the 25th International Conference on Machine Learning . ACM, 2008.
- Srivastava N. et al. Dropout: a simple way to prevent neural networks from overfitting //The journal of machine learning research. — 2014. — Т. 15. — №. 1. — С. 1929–1958
- Srivastava N. Improving neural networks with dropout //University of Toronto. — 2013. — Т. 182. — №. 566. — С. 7.
- Сикорский О. С. Обзор свёрточных нейронных сетей для задачи классификации изображений //Новые информационные технологии в автоматизированных системах. — 2017. — №. 20. — С. 37–42.
- Csáji B. C. et al. Approximation with artificial neural networks //Faculty of Sciences, Etvs Lornd University, Hungary. — 2001. — Т. 24. — №. 48. — С. 7.
- Тимонин В. А., Демьянов В. В., Каневский М. Ф. Нелинейной оптимизации для обучения инс многослойный перцептрон. Препринт № IBRAE-99–09. Москва: Институт проблем безопасного развития атомной энергетики РАН. 1999. 28 с. Библиогр.: 15 назв. — 1999. (http://www.ibrae.ac.ru/docs/109/mlp.pdf)
- Шишкин А. Г. Распознавание стиля произведений живописи по их изображениям с помощью глубоких нейронных сетей //Интеллектуальные системы. — 2020. — №. 3. — С. 65. (https://ics.pnu.edu.ru/media/2020/N65_07.pdf)
- G. Hinton and R. Salakhutdinov. Reducing the dimensionality of data with neural networks. Science , 313(5786):504–507, 2006.
- R. Salakhutdinov and G. Hinton. Deep Boltzmann machines. In Proceedings of the International Conference on Artificial Intelligence and Statistics, volume 5, pages 448–455, 2009.
- Ba J., Frey B. Adaptive dropout for training deep neural networks //Advances in neural information processing systems. — 2013. — Т. 26.