Обзор и применение квантового алгоритма Шора в дешифровании в системах криптографии, основанных на эллиптических кривых



В данной работе рассмотрен метод дешифрования систем, основанных на эллиптических кривых — квантовый алгоритм Шора.

Ключевые слова: криптография, квантовый компьютер, кубит.

В ближайшем будущем ожидается переход от классических вычислений к квантовым. Одна из первых моделей квантового компьютера была предложена Р. Фейнманом в 1981 г. [1]. Квантовый компьютер использует для вычисления не обычные (классические) алгоритмы, а процессы квантовой природы, так называемые квантовые алгоритмы, использующие квантово-механические эффекты — квантовый параллелизм и квантовая запутанность. Если классический компьютер в каждый момент времени может находиться только в одном состоянии , то квантовый процессор может находиться одновременно в обоих этих состояниях с различной комплексной амплитудой (1):

(1)

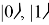
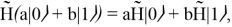
где — комплексные амплитуды, определяющие вероятность получения результата измерения. Это состояние квантовой суперпозиции будем называть кубитом (от англ. quantum bit) [2].

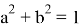
Иные фундаментальные основы квантовой информатики требуют иного подхода в том числе и к криптографии. Одним из современных методов шифрования информации является использование эллиптических кривых.

Эллиптическая кривая — это плоская кривая, описываемая уравнением (2):

,(2)

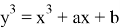
где для отсутствия на кривой особых точек [3]. Пример такой кривой приведен на рис. 1.

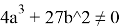
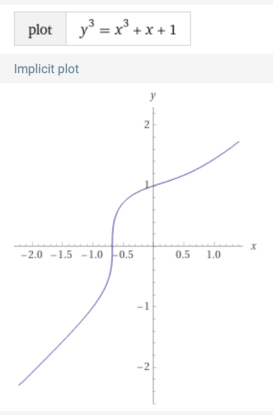
Рис. 1. Эллиптическая кривая с

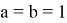
На использовании эллиптических кривых, например, основывается ГОСТ 34.10–2018 [4], регламентирующий создание и проверку цифровой подписи.

Классическими средствами данный метод шифрования практически не дешифруем. Однако ситуация меняется при использовании квантовых вычислений. Шифрование с использованием эллиптических кривых уязвимо к использованию алгоритма Шора — квантового алгоритма, предназначенного для факторизации (разложения числа на простые множители), позволяющий разложить число за время

, используя вместо логических кубитов [5].

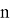
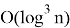
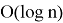
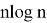
Алгоритм Шора имеет вероятностный характер. Первый источник случайности встроен в классическое вероятностное сведение разложения на множители к нахождению периода некоторой функции. Второй источник появляется из необходимости наблюдения квантовой памяти, которое также даёт случайные результаты.

Данный алгоритм в основе своей сводится к перебору вариантов. Схематически его можно разделить на два этапа:

1) Классический

2) Квантовый

В классическом этапе разложения числа используется случайный параметр , такой что и

(наибольший общий делитель). Если в выражении (3) можно вычислить как функцию , то можно найти собственный делитель за время, ограниченное полиномом от с вероятностью для любого фиксированного .

(3)

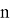
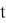
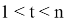
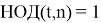
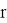
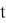
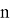
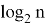
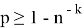
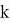
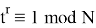
Для осуществления квантовой части алгоритма вычислительная схема представляет собой два квантовых регистра , первоначально находящихся в нулевом состоянии

. Регистр используется для записи аргументов функции . Регистр используется для записи значений функции , период которой будет вычисляться. Квантовый этап состоит из 4 шагов:

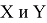
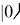
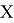
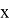
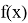
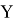
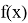
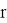
1) Перевод начального состояния регистра в суперпозицию всех битовых состояний (размер регистра памяти), регистр

остается в состоянии . Результирующее состояние системы двух регистров (4):

(4)

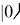
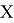
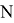
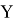
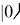
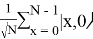
2) Применение унитарного преобразования , переводящее в (5):

(5)

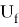
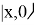
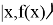
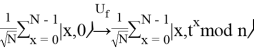
3) Применение квантового Фурье-преобразования к (5). В двумерной плоскости

это соответствует повороту осей на 90, что приводит к преобразованию шкалы в шкалу (6):

(6)

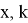
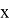
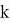
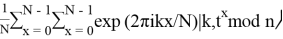
4) Измерение регистра относительно ортогональной проекции вида , где — тождественный оператор регистра на гильбертовом пространстве.

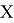
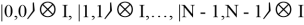
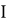
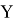
В результате получаем

c вероятностью (7):

(7)

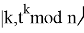
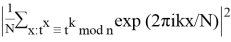
Далее находим наилучшее приближение снизу к со знаменателем

(8):

(8)

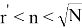
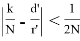
Пробуем в качестве

. В случае четного , то вычисляется

. Если нечетно, то расчет следует повторить раз с тем же .

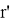
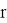
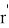
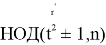
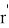
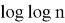
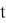
Литература:

1. Feynman R. Simulating Physics with Computers (англ.) // International Journal of Theoretical Physics — Springer Science+Business Media, 1982. — Vol. 21, Iss. 6 / 7. — P. 467–488. — ISSN 0020–7748; 1572–9575 — doi:10.1007/BF02650179
2. Щука А. А. Наноэлектроника: учебник для бакалавриата и магистратуры — М.: Издательство Юрайт, 2017. — 297 с.
3. Joseph H. Silverman. The Arithmetic of Elliptic Curves. — N. Y.: Springer, 2009. — P. 42–43,59,137–138. — 408 p. — ISBN 978–0–387–09493–9.
4. ГОСТ 34.10–2018. Информационная технология. Криптографическая защита информации. Процессы формирования и проверки электронной цифровой подписи — М.: Стандартинформ, 2018. — 16 с.
5. Shor P. Algorithms for Quantum Computation: Discrete Logarithms and Factoring (англ.) // Foundations of Computer Science, 1994 Proceedings., 35th Annual Symposium on — IEEE, 1994. — P. 124–134. — ISBN 0–8186–6580–7 — doi:10.1109/SFCS.1994.365700