Определение очертаний береговой линии с помощью радиолокационных средств имеет чрезвычайно важное значение, особенно для островных государств. При синтезе алгоритмов обработки сигналов, отраженных от береговой кромки, необходимо учитывать закон распределения вероятностей мощности сигналов, являющийся векторной суммой сигналов, отраженных от поверхности моря и земной поверхности. В работе представлен алгоритм моделирования подобных сигналов.
Ключевые слова : береговая кромка, распределение вероятностей, земная поверхность, морская поверхность, алгоритм моделирования.
The delineation of coastlines by radar is of the utmost importance, especially for island states. When synthesizing algorithms for processing signals reflected from the coastal edge, it is necessary to take into account the law of probability distribution of signal power, which is the vector sum of signals reflected from the sea surface and the earth's surface. The paper presents an algorithm for modeling such signals.
Keywords : coastal edge, earth surface, modeling algorithm, probability distribution, sea surface.
В последнее время наблюдается постоянное потепление климата, что приводит к таянию высокогорных ледников и ледников полюсов земли. В силу этого повышается уровень мирового океана и изменяются очертания береговых линий. Кроме этого очертания береговых линий изменяются и в результате таких природных явлений как извержения вулканов, тайфуны, оползни, а также и в результате деятельности людей, в частности, искусственного намывания грунта с целью расширения сухопутных зон. Поэтому современному обществу необходимо осуществлять постоянный мониторинг изменения береговых линий.
В работе [1] были изложены физические особенности отражения локационных сигналов от поверхности элемента разрешения бортовой аппаратуры [2], в который входят поверхность моря и поверхность суши. В качестве математических моделей эхо-сигналов береговой кромки были использованы наиболее распространенные модели отражений от земли и моря: для поверхности земли принято распределение флюктуаций мощности отраженных сигналов, подчиняющееся распределению Вейбулла, а для морской поверхности — логарифмически-нормальному распределению [3].
В работах [4, 5, 6, 7] были представлены результаты анализа алгоритмов определения береговой кромки при разных условиях её наблюдения. При моделировании распределений Вейбулла [8] и логарифмически-нормального [9] распределения считалось, что временная корреляция эхо-сигналов в отраженных пачках импульсов отсутствует, что соответствует условию использования быстрой перестройки частоты, несущей зондирующих импульсов [10, 11]. В данной работе снимается это ограничение и приводятся алгоритмы моделирования флюктуаций мощности при коррелированных последовательностях эхо-сигналов, отраженных от кромки.
В работе [1] представлена модель локационного сигнала, отраженного от кромки земля-море, кратко опишем эту модель. Пусть в элемент разрешения бортовой аппаратуры, соответствующий кромке, площадь которого равна
S
, попадают фрагменты морской и земной поверхностей, площади которых соответственно равны

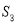

где

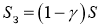
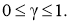
Тогда амплитуда локационного сигнала A , отраженного от такого элемента, определяется векторной суммой сигналов, отраженных от земной и морской поверхностей [3]

где
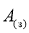
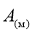
Плотностью распределения вероятностей амплитуды
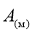
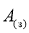
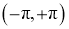
Для моделирования потока данных
A
i
, необходимо моделировать три потока
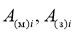
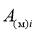
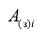
Моделирование потока фаз φ
i
тривиально, при моделировании потоков
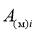
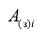
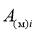
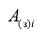
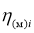
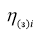
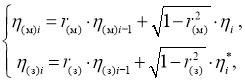
где
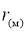
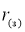
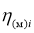
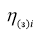
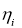

Алгоритм моделирования потоков
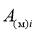
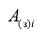
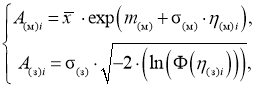
параметры распределений, которые определяются через удельные эффективные отражающие поверхности земли и моря [13], а Ф(.) — табулированная функция распределения вероятностей нормального распределения с нулевым средним и единичной дисперсией. Нормированные корреляционные функции последовательностей
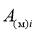
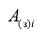
Литература:
- Исаков В. И., Шепета Д. А. Моделирование локационных сигналов, отраженных от кромки земля-море. // Информационно-управляющие системы. — 2017. — № 5. — C. 89–94.
- Изранцев В. В., Шепета Д. А. Моделирование внешних сигналов бортовых приборных комплексов летательных аппаратов пятого поколения // Научное приборостроение. — 2000. — Т.10. — № 2. — С. 14–19.
- Исаков В. И., Шепета Д. А. Плотность распределения мощности огибающей локационных сигналов, отраженных от кромки земля-море // В книге: Обработка, передача и защита информации в компьютерных системах. XXV Международной научная конференция: сборник докладов. Санкт-Петербург, 2021. — С. 25–28.
- Nenashev V. A., Shepeta D. A., Isakov V. I. Modeling of Input Signals Reflected from Coastal Zones and Observed by Small-Sized Radar Systems from UAVS // Journal of Applied Remote Sensing. — 2022. — T.16. — № 1. — C. 012015.
- Nenashev V. A., Shepeta D. A. Мathematical models and algorithms for modeling the location signals reflected from the underlying surfaces of the earth, sea, and coastal waters, Proc. SPIE Remote Sensing of the Ocean, Sea Ice, Coastal Waters, and Large Water Regions, Strasbourg, France. — 2019. — Pp. 111501V-1–111501V-6
- Wattimena G. M., Nenashev V. A., Shepeta D. A. Mathematical Model of Location Signal Reflections from The Substrate Surface of The Sea Observed By On-Board Radar // Proceedings of The 2nd International Conference On Advance And Scientific Innovation, ICASI 2019, 18 July, Banda Aceh, Indonesia. — Pp. 1–9.
- Wattimena G. M., Shepeta D., Isakov V. Determination of the Coastal Edge Using on Board Radar // Proceeding of SPIE — The International Society for Optical Engineering. — Tokyo, Japan, — 2021. — C. 119140D.
- Шепета, Д. А. Алгоритм моделирования коррелированных числовых последовательностей, распределенных по закону Вейбулла / Д. А. Шепета, В. В. Боженко, Е. Н. Долгов // Волновая электроника и инфокоммуникационные системы: Сб. ст. XXV Междунар. науч. конф. — Санкт-Петербург: Санкт-Петербургский государственный университет аэрокосмического приборостроения, 2022. — С. 130–134.
- Шепета, Д. А. Прямой метод моделирования логарифмически-нормального распределения / Д. А. Шепета, В. И. Исаков, В. А. Тюринова // Волновая электроника и инфокоммуникационные системы: Сб. ст. XXV Междунар. науч. конф. — Санкт-Петербург: Санкт-Петербургский государственный университет аэрокосмического приборостроения, 2022. — С. 135–139.
- Подоплёкин Ю. Ф., Шепета Д. А. Имитационные модели и математическое моделирование эхо-сигналов кораблей и морского фона // Морская радиоэлектроника. — 2021. — № 2 (76). — С. 54–57.
- Шепета А. П., Махлин А. М. Декорреляция эхо-сигналов морской поверхности при перестройке несущей частоты бортовой РЛС // Морская радиоэлектроника. — 2020. — № 1 (71). — С.36–38.
- Шепета Д. А. Разработка математических моделей и синтез алгоритмов моделирования входных сигналов бортовых систем обработки информации и управления. Диссертация на соискание ученой степени кандидата технических наук / Санкт-Петербург, 2000.
- Блаунштейн Н. Ш., Сергеев Б. М., Шепета А. П. Прикладные аспекты электродинамики. — СПб.: Аграф+, 2016. — 272 с., ил.
- Шелухин О. И., Беляков И. В. Негауссовские процессы. — СПб.: Политехника, 1992. — 312 с., ил.







