Для оценки параметров регрессионных кривых в подавляющем большинстве случаев используется метод наименьших квадратов, поскольку предполагается, что ошибки в данных распределены по нормальному закону. На этом же предположении строятся и доверительные интервалы, позволяющие оценить значимость полученных оценок. При негауссовых ошибках оценить значимость полученных оценок можно путем математического моделирования. В работе рассматривается алгоритм моделирования негауссовых ошибок в соответствии с моделью Хьюбера.
Ключевые слова : регрессионная кривая, нормальный закон, математическое моделирование, модель Хьюбера.
To estimate the parameters of regression curves in the vast majority of cases, the method of least squares is used, since it is assumed that the errors in the data are distributed according to a normal law. On the same assumption, confidence intervals are built. Those are allowing us to assess the significance of the estimates obtained. In cases of non-Gaussian errors, it is possible to assess the significance of the estimates obtained by mathematical modeling. The paper deals with an algorithm for modeling non-Gaussian errors in accordance with the Huber model.
Keywords : Huber model, mathematical modeling, normal law, regression curve.
Зависимость между случайными величинами в экономических исследованиях оценивают по кривым регрессии, представляющими собой условное среднее вычисляемое для эндогенной переменной при конкретных значениях экзогенных переменных [1]. При вычислении этой функциональной зависимости необходимо знать совместный многомерный закон распределения эндогенных и экзогенных случайных величин, который на практике неизвестен. Поэтому, кривые регрессии оценивают приближенно, используя для аппроксимации кривых эмпирические данные, по которым и строится оценка регрессионной зависимости.
Наиболее распространенным методом аппроксимации кривых регрессии является метод наименьших квадратов, позволяющий при задании функционального вида аппроксимирующей кривой, оценить её параметры [1]. Критерием близости аппроксимирующей кривой к эмпирическим данным выступает минимум суммы квадратов ошибок. При этом в подавляющем большинстве случаев при использовании этого критерия предполагается нормальный закон распределения помех.
Этот метод фактически использует следующую известную теорему: пусть случайная величина ξ имеет закон распределения вероятностей, для которого существуют среднее значение m ξ и дисперсия D ξ , тогда среднее значение квадрата разности M((ξ-c) 2 ) достигается при c=m ξ , то есть минимальное значение достигается при константе с равной математическому ожиданию m ξ и равно, как это следует из вышеприведенного выражения, дисперсии D ξ случайной величины ξ .
Следует заметить, что этот метод хорош лишь при нормальном законе распределения ошибок, поскольку для нормальных помех он является и методом максимального правдоподобия. Точнее, он является наилучшим в классе всех линейных оценок для ошибок, закон распределения которых относится к обобщенному экспоненциальному распределению, частным случаем которого является нормальный закон распределения [2].
В том случае, когда помехи имеют другой, отличный от нормального, закон распределения, этот метод может оказаться неустойчивым и привести, соответственно, к некорректным оценкам, особенно если закон распределения помех относится к законам с «утяжеленными» хвостами распределения.
Поэтому, если у исследователя нет уверенности в нормальном законе распределения ошибок, необходимо использовать и другие методы оценки параметров регрессионных кривых. В этом случае наиболее часто используется критерий оценки параметров кривой регрессии по методу минимизирующему сумму абсолютных отклонений — метод минимума суммы модулей. Этот метод относится к робастным методам обработки информации, поэтому он мало чувствителен к закону распределения ошибок [3].
Метод минимума суммы модулей отклонений основан на следующей теореме: пусть случайная величина ξ имеет некоторый закон распределения вероятностей, тогда среднее значение модуля разности M(|ξ-c|) достигается при константе с , равной медиане распределения с= μ ξ . Необходимо отметить, что медиана распределения существует всегда, а существование среднего значения и дисперсии распределения для этого критерия, в отличие от предыдущего, не требуется. В частности, метод наименьших модулей можно использовать даже в том случае, когда ошибки распределены по закону Коши, для которого не существует ни среднего, ни дисперсии [4]. Попытка в этой ситуации использовать метод наименьших квадратов приведет к тому, что по конечной выборке будут определены численные значения «псевдосредних» и «псевдодисперсий», которые никакого значения и смысла не имеют.
Необходимо отметить, что метод минимума суммы модулей отклонений не очень сильно «проигрывает» методу наименьших квадратов, в том случае, когда ошибки имеют нормальный закон распределения. Если же ошибки распределены не по нормальному закону, особенно в том случае, когда закон распределения ошибок относится к законам с утяжеленными хвостами распределения, метод наименьших модулей может значительно «выиграть» у метода наименьших квадратов в смысле оценки точности определения параметров аппроксимирующей регрессионной кривой.
Из всего сказанного выше следует, что на практике, при задании функционального вида кривой аппроксимирующей кривую регрессии, желательно кроме традиционного метода наименьших квадратов при обработке эмпирических данных, использовать и метод наименьших модулей. Если при этом параметры аппроксимирующей кривой, определенные этими двумя методами, различаются не сильно, то можно использовать оценки доверительных интервалов для параметров кривой, использующие нормальный закон распределения ошибок [1], и, соответственно, оценивать значимость полученных результатов.
В теоретических же исследованиях, желательно ещё и исследовать устойчивость полученных оценок при отклонении закона распределения от нормального, то есть желательно оценивать и робастность используемых алгоритмов, которая будет зависеть не только от алгоритма, но и от вида кривых, используемых для аппроксимации исследуемых зависимостей.
В подобных исследованиях используются специальные составные распределения модель Тьюкки — в виде весовой суммы нормальных распределений с разными дисперсиями, и модель Хьюбера, которая является обобщением модели Тьюкки, — весовая сумма произвольных распределений. При этом следует отметить, что исследование робастности проводится методами математического моделирования [5], что и позволяет исследовать практически любые зависимости при любых законах распределения ошибок.
Для модели Тьюкки плотность распределения помех f ξ (x) записывается в виде
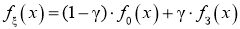
где f 0 (x) — основное (гипотетическое) распределение помех, f 3 (x) — «засоряющее» распределение, γ коэффициент засорения. В модели Тьюкки оба распределения f 0 (x) и f 3 (x) нормальные с нулевыми средними, но разными дисперсиями. Дисперсия засоряющего распределения намного больше дисперсии основного, что и приводит к появления «хвостов» распределения f ξ (x) . Эта модель наиболее широко используется в экономических исследованиях при оценке робастности алгоритмов обработки информации.
Модель Хьюбера, определяемая тем же выражением (1), является обобщением модели Тьюкки, в котором основное f 0 (x) и засоряющее f 3 (x) распределения могут иметь произвольный вид, отличный от нормального. Однако модификация модели Хьюбера для её применения в экономических исследованиях состоит в том, что основное распределение f 0 (x) остаётся нормальным, а засоряющее f 3 (x) — отлично от нормального. В качестве засоряющего распределения в этом случае предлагается использовать распределение вида
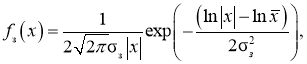
параметры которого x̅ и ϭ ξ можно определить, используя результаты, изложенные в работе [6]. У этого распределения среднее, в силу симметрии распределения, равно нулю, а дисперсия равна удвоенной дисперсии логарифмически-нормального распределения, что и обеспечивает «утяжеленные» симметричные хвосты распределения помех f ξ (x) .
В заключение отметим, что изложенная модификация распределения Хьбера позволяет учитывать как небольшие отличия распределения помех от нормального (гипотетического), так учитывать и выбросы, которые могут считаться аномальными.
Литература:
- Айвазян С., Мхитарян В., Прикладная статистика, Основы эконометрики (в 2-х томах), М.: ЮНИТИ-ДАНА, 2001–2-е изд., испр., с. 656+432.
- Леман Э. Проверка статистических гипотез: Пер. с англ Ю. В. Прохорова. — М.: Наука, 1979, 408 с., ил.
- Хьюбер Дж. П. Робастность в статистике / Пер. с англ. — М.: Мир, 1984. — 304 с., ил.
- Кобзарь А. И. Прикладная математическая статистика. Для инженеров и научных работников. — М.: ФИЗМАТЛИТ, 2006. — 816 с.
- Шепета Д. А. Разработка математических моделей и синтез алгоритмов моделирования входных сигналов бортовых систем обработки информации и управления. Диссертация на соискание ученой степени кандидата технических наук / Санкт-Петербург, 2000.
- Шепета, Д. А. Прямой метод моделирования логарифмически-нормального распределения / Д. А. Шепета, В. И. Исаков, В. А. Тюринова // Волновая электроника и инфокоммуникационные системы: Сб. ст. XXV Междунар. науч. конф. — Санкт-Петербург: Санкт-Петербургский государственный университет аэрокосмического приборостроения, 2022. — С. 135–139.







