Спектр задач в области телекоммуникаций и анализа данных все время расширяется. Появляются новые методы анализа путей в сети и сложных сетевых структур, новые методики и алгоритмы построения и анализа сетей, одной из них является применение лабиринтов. Методы построения и прохождения лабиринтов можно применять для моделирования сетевых структур, нахождения оптимальных путей, упрощения анализа состояния сложных структур. В статье представлены результаты исследований в данной области.
Ключевые слова : лабиринт, алгоритм построения, алгоритм обхода.
The range of tasks in the field of telecommunications and data analysis is expanding all the time. New methods for analyzing paths in a network and complex network structures are emerging, new methods and algorithms for building and analyzing networks are emerging, one of them is the use of labyrinths. Labyrinth construction and traversal methods can be used to model network structures, find optimal paths, and simplify the analysis of the state of complex structures. The article presents the results of research in this area.
Keywords : mazes, construction algorithm, traversal algorithm.
Сегодня применение алгоритмов построения и прохождения лабиринтов улучшает оптимизацию и логику построения различных технических и математических объектов. Известен ряд литературных источников, посвященных данной тематике [1–7], но вопросам скорости обработки лабиринтов уделяется мало внимания. Применение лабиринтов в последнее время сказывается в разных технических областях. Они используются для трассировки печатных плат, в игровой индустрии — при создании динамических маршрутов и путей движения игроков, в телекоммуникациях для нахождения самых быстрых и самых коротких путей прохождения сетей, в горнодобывающей промышленности для оптимального построения шахт и др. Применение лабиринтов бывает и прикладное, например для обучения систем искусственного интеллекта [8]. Также применение методов и алгоритмов построения и прохождения лабиринтов может использоваться для построения оптимальной структуры сети, как сточки зрения минимальной длины, так и с точки зрения минимального количества энергии, требуемой для передачи данных. При анализе сетей также возможно использование многокритериального анализа. Удобство применения лабиринтов в различных областях обусловлено возможностью их бинаризации, представления в виде одного или нескольких массивов данных, с возможностью выполнения их последующей обработки и применении к ним методов оптимизации.
Рассмотрим характеристики лабиринтов подробнее. При создании лабиринтов требуется применять некоторые общие правила, такие как: отсутствие замкнутых контуров или петель, отсутствие изолированных от других частей лабиринта областей, наличие определенное количество входов и выходов для неидеальных лабиринтов. Для создания идеальных лабиринтов существует несколько типов алгоритмов. Первый основан на методике выращивания идеального лабиринта в качестве дерева, второй основан на удалении клеток для построения лабиринта, третий на основе клеточных автоматов. Тупики являются необходимым показателем сложности прохождения лабиринта. При росте количества тупиков их длина будет уменьшаться. Желательно, чтобы тупики были длинные и их было как можно больше, но с ростом количества тупиков их количество будет уменьшаться. Поэтому, существуют оптимальные границы количества ячеек тупиков для лабиринтов, которые могут варьироваться от поставленной задачи, например, от 10 до 30 процентов общего числа ячеек лабиринта. Было проведено тестирование более десяти алгоритмов построения лабиринтов. С точки зрения количества созданных тупиков, самыми лучшими алгоритмами стали алгоритм растущего дерева и алгоритм Прима.
Еще одной характеристикой лабиринта является смущенность проходов. Смещенностью обладают все алгоритмы, например наименьшая смущенность может быть реализована в спиральном алгоритме, большая смещенность достигнута в алгоритмах двоичного дерева. Однородность лабиринта характеризуется одинаковой плотностью заполнения (или разрежения) ячеек, однородными могут лабиринты со слабой смещенностью, хорошей однородностью обладает, например алгоритм Эллера.
Дополнительной характеристикой при построении лабиринтов является объем памяти необходимой для работы алгоритма. Для работы качественных алгоритмов требуются битовые карты лабиринтов или только одна ячейка, как в алгоритме двоичного дерева. Часть алгоритмов использует память пропорционально длине массива, например Эллера; другие имеют кввадратичную зависимость, например, алгоритм растущего дерева или Краскала. При рекурсивном делении используется память размером длины строки, для подобных алгоритмов можно применять стек. Необходимым параметром для лабиринтов является извилистость или процент ячеек, по которым проходит путь решения. Чем больше извилистость, тем сложнее лабиринт, так наибольшую извилистость имеют одномаршрутные лабиринты, а наименьшую — алгоритмы двоичного дерева, когда решение просто проходит насквозь лабиринт.
Размерность лабиринта является основной характеристикой лабиринта, так как от этого могут зависеть методы его построения и прохождения. Бывают двухмерные трехмерные и многомерные лабиринты. При построении и прохождении многомерных лабиринтов для ускорения процесса можно использовать монопоточное и параллельное программирование. Также для изучения топологий и свойств четырехмерного пространства можно использовать лабиринты соответствующей размерности. Скорость обработки данных по лабиринтам в распределенных приложениях обусловлена количеством физических потоков в ядрах процессоров и некоторой тратой времени на синхронизацию процессов.
Результаты исследований
Рассмотрим применяемые в работе алгоритмы подробнее. Были исследованы более двадцати разных алгоритмов генерации и прохождения лабиринтов. На рис. 1–2 показаны результаты экспериментов по поиску путей в идеальных и неидеальных лабиринтах, а также на рис.3 результаты генерации идеальных лабиринтов.
На рис. 1 показаны графики работы алгоритмов, сверху вниз: Евклида, А* с манхеттенским расстоянием, А* с расстоянием Чебышева, поиск в ширину.
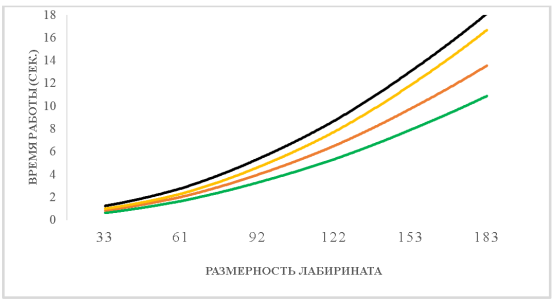
Рис. 1. Поиск путей в идеальных лабиринтах
На рис. 2 показаны графики работы алгоритмов, сверху вниз: Дейкстры, А* с манхэттенским расстоянием, А* с расстоянием Чебышева, поиск в ширину.
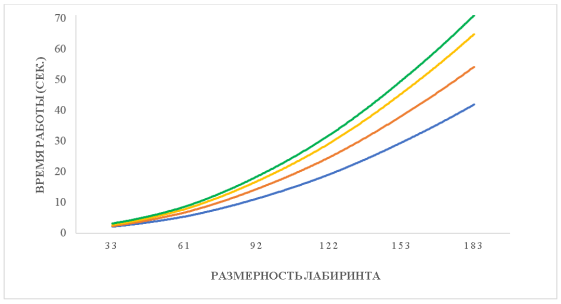
Рис. 2. Поиск путей в неидеальных лабиринтах
На рис. 3 показаны графики работы алгоритмов, сверху вниз: Прима (модифицированный) [7], бинарное дерево [2], Backtracking [1], рекурсивное деление [3], Sidewinder. Как видно из графиков, скорость генерации и прохождения лабиринтов имеет одинаковую размерность, что обусловлено схожестью эвристических алгоритмов. Часть алгоритмов ввиду их небольшой скорости работы не были представлены на рис. 1–3.
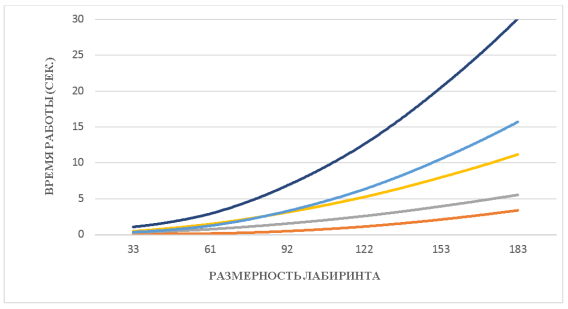
Рис. 3. Генерация идеальных лабиринтов
Выводы
Применение алгоритмов построения лабиринтов и в общем случае графов, может быть востребовано в любых технических областях, с точки зрения оптимальной структуры связей компонентов, скорости и объема прохождения информации, изучения горных пород, медицинских исследований. В результате проделанной работы были реализованы эвристические алгоритмы генерации и прохождения лабиринтов. Наиболее быстрыми алгоритмами построения идеальных лабиринтов оказались алгоритмы Sidewinder и рекурсивного деления. Так алгоритмы на основе дерева, например, алгоритм двоичного дерева создает неоднородную структуру лабиринта со смещением по диагонали. Алгоритмы на базе множеств, строят лабиринты с произвольными множествами, которые потом объединяют друг с другом.
Следует отметить, что самыми быстрыми алгоритмами генерации неидеальных лабиринтов является змеевидный лабиринт и алгоритм маленьких комнат. Наиболее быстрыми алгоритмами построения деревьев были алгоритмы A* и алгоритм поиска в ширину. Следует отметить, что сложные лабиринты могут быть получены не только определенными алгоритмами, но и путем применения нескольких алгоритмов, которые с определенной логикой будут чередоваться или применять решающее правило построения, например, используя нечеткую логику. Следующим этапом исследования лабиринтов может быть применение муравьиных, генетических алгоритмов и алгоритмов роевого интеллекта при прохождении неидеальных лабиринтов, также применение программной многопоточности при реализации алгоритмов.
Литература:
- Backtracking algorithm. — Текст: электронный / J. Buck // The Buckblog: [сайт]. — URL: https://weblog.jamisbuck.org/2010/12/27/maze-generation-recursive-backtracking (дата обращения: 01.11.2022).
- Binary Tree algorithm. — Текст: электронный / J. Buck // The Buckblog: [сайт]. — URL: https://weblog.jamisbuck.org/2011/2/1/maze-generation-binary-tree-algorithm (дата обращения: 01.11.2022).
- Division algorithm. — Текст: электронный / J. Buck // The Buckblog: [сайт]. — URL: https://weblog.jamisbuck.org/2011/1/12/maze-generation-recursive-division-algorithm (дата обращения: 01.11.2022).
- Eller's algorithm. — Текст: электронный / J. Buck // The Buckblog: [сайт]. — URL: https://weblog.jamisbuck.org/2010/12/29/maze-generation-eller-s-algorithm (дата обращения: 01.11.2022).
- Growing Tree algorithm. — Текст: электронный / J. Buck // The Buckblog: [сайт]. — URL: https://weblog.jamisbuck.org/2011/1/27/maze-generation-growing-tree-algorithm (дата обращения: 01.11.2022).
- Kruskal's algorithm. — Текст: электронный / J. Buck // The Buckblog: [сайт]. — URL: https://weblog.jamisbuck.org/2011/1/3/maze-generation-kruskal-s-algorithm (дата обращения: 01.11.2022).
- Prim's algorithm. — Текст: электронный / J. Buck // The Buckblog: [сайт]. — URL: https://weblog.jamisbuck.org/2011/1/10/maze-generation-prim-s-algorithm (дата обращения: 01.11.2022).
- Mazes creation for further study of swarm intelligence / A. V. Dagaev, A. A. Sorokin, R. A. Kovalenko, E. A. Yakovleva // IOP Conferences Series: Materials Science and Engineering. — 2020. — Vol. 919. — 52058.







