Поиск пути в трехмерном пространстве

В рамках данной работы рассматривается вопрос нахождения оптимального пути между двумя точками в трехмерном пространстве, рассматриваются соответствующие методы решения.

Ключевые слова: оптимальный путь, трехмерное пространство, критерии оценки, алгоритмы поиска, граф, навигация.

Within the framework of this work, the question of finding the optimal path between two points in three-dimensional space is considered, the corresponding solution methods.

Keywords: optimal path, three-dimensional space, evaluation criteria, search algorithms, graph, navigation.

Поиск пути — задача определения оптимального маршрута между двумя точками в пространстве. Оптимальность в данном вопросе зависит от поставленной задачи. Основной критерий — избежать препятствия на выбранном маршруте. Поиск пути в 3D-пространстве с препятствиями — важная проблема в системах виртуальных миров, чаще всего встречающаяся в их прикладном применении — навигация в компьютерных играх.

Рассмотрим существующие методы решения. При нахождении оптимального пути выделяют несколько основных алгоритмов. Так как не существует точного метода, то алгоритмы, которые будут рассматриваться, являются вариантами алгоритма А*.

Алгоритма А* подразумевают что для представления местности используется виртуальная сетка. Сетка состоит из клеток одинаковой формы. Для каждой клетки задается свойство, проходима эта клетка или нет. Движущийся объект (персонаж) на виртуальной сетке занимает одну клетку [1]. Алгоритм часто используется для представления 2D-пространства, однако при использовании в 3D-пространстве выявляются существенные недостатки:

— в трехмерном пространстве объекты часто имеют произвольную форму, например если рассмотреть трехмерное пространство как некий 3D-мир в компьютерной игре, то объекты, будь то дома, ландшафтные строения имеют произвольную форму, в зависимости от дизайна, и плохо ложатся на виртуальную сетку пространства;

— 3D-мир подразумевает существование объектов, которые могут перемещаться — динамических препятствия. При перемещении этих объектов может возникнуть ситуация, когда объект, ранее занимал одну клетку, в результате перемещения и взаимодействия с другими объектами займет более одной клетки, например пять клеток;

— при перемещении в трехмерном пространстве необходимо учитывать и методы сглаживания сплайнами, в результате использования этих методов может возникнуть ситуация с непроходимостью отдельный участков маршрута;

Метод навигационного графа (НГ) рассматривает 3D-мир, как некий граф, в котором ребра графа соединяют вершины (трехмерные точки). Упрощенные варианты его реализации для плоскости приведены на рис. 1. и 2. Принято считать, что все ребра проходимы, т. е. условный персонаж в виртуальном мире может по ним пройти и не встретить на своем пути какое-либо препятствие. Задача выглядит следующим образом — необходимо найти вершину, которая будет ближайшей относительно начальной точки и также найти вершину и для конечной точки. Строится оптимальный путь с учетом критерия минимального веса [2].

Рис. 1. Примеры навигационных графов [1]

Рис. 2. Примеры использования навигационных графов [1]

Недостатки:

— трудоемкость, в определенных ситуациях количество вершин графа велико, а при большом исходном 3D-мире это количество чрезмерно;

— появляется «неестественная траектория» движения объекта (персонажа);

— учитывается только один размер объекта, а при перемещении объектов различных размеров (движущиеся объекты в 3D-мире) возникают трудности, т. к. размещение вершин графа ориентировано на один конкретный размер объекта.

Метод сочетания эвристик подразумевает использование некого алгоритма решения «проблемной» ситуации при обходе препятствия. Например, этот алгоритм можно рассмотреть, так: в ситуации, когда условный персонаж может столкнуться с неким препятствием (рис. 3) нужно построить луч, отклонение которого будет минимальным относительно вектора «взгляда» персонажа, при этом этот вектор не должен пересекаться с объектами 3D-мира. При нахождении такого луча персонаж перемешается и продолжает путь по прямому маршруту к конечной точке.

Рис. 3. Общая вершина в навигационном графе множества подвижных объектов, где любой объект может стать препятствием для других

Недостатки:

— большая сложность разрешения ситуации при столкновении с объектом, сложность зависит от числа 3D-полигонов;

— существует возможность, что правильный пусть не будет найден.

Развитие методов решения — учитывать как статические, так и динамические объекты, изменять состояние проходимости ребра, учесть момент столкновения в момент следования к конечному пункту, проанализировать расположение динамических объектов на ребрах со статическими объектами, использовать не один НГ, а несколько, количество зависит от количества объектов и размера 3D-мира, а критерии например создание временного НГ для пересекающихся НГ, слияние НГ и т. д. Так, например, в средстве построения виртуальных миров Unity предлагается создание «навигационной поверхности» (рис. 4) в которой процедурой «запекания» исключаются статичные объекты. А уже для остальных задач — прокладка маршрута и обход динамических препятствий — используются классические алгоритмы, предлагаемые самим Unity или реализованные разработчиком.

Рис. 4. Система навигации Unity [3]

Сложность базируется на следующих шагах:

1) число динамических объектов, у которых изменилась позиция и угол поворота:

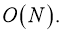
2) измененные координаты вершин НГ динамических объектов:

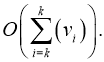
3) поиск пересекающихся динамических объектов:

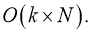
Литература:

1. Pathfinding in 3d space — A*, Theta*, Lazy Theta* in octree structure. — Текст: электронный / C.-M. Hung // Chia-Man Hung: [сайт]. — 2016. — URL: https://ascane.github.io/assets/portfolio/pathfinding3d-report.pdf (дата обращения 05.11.2022).
2. Алексеев, В. Е. Дискретная математика: учеб. пособие. — Нижний Новгород: Нижегородский госуниверситет, 2017. — 139 с.
3. Build VR: Using Unity NavMesh for First Person Movement in VR. — Текст: электронный / D. Jonston // Medium — Where good ideas find you: [сайт]. — 2018. — URL: https://medium.com/@davijoh73/build-vr-using-unity-navmesh-for-first-person-movement-in-vr-64efe0909d84 (дата обращения 05.11.2022).