В статье рассматривается использование математической модели инвестирования в портфель ценных бумаг нескольких компаний, учитывая риски как финансовые, так и нефинансовые.
Ключевые слова: прогноз, математическая модель, риск, кризис, акции.
The article discusses the use of a mathematical model for investing in a portfolio of securities of several companies, taking into account both financial and non-financial risks.
Keywords: forecast, mathematical model, risk, crisis, shares.
До сих пор не потерян интерес к выгодному размещению средств. Эта проблема каждым решается по-своему. Одним из привлекательных способов инвестирования является помещение сбережений в ценные бумаги, то есть формирование портфеля ценных бумаг.
Конечно, необходимо рассмотреть более выгодные на текущий момент направления инвестирования, для получения большего дохода с учетом различных финансовых факторов и рисков. Кроме финансовых рисков следует учитывать и кризисные изменения — политические, социальные [1].
Раннее в [2] была рассмотрена математическая модель, учитывающая нестабильность социальных и политических состояний, в которой прогнозировалась прибыль от вложенных бумаг с учетом не только финансовых факторов, но и таких как возникновение пандемии, объявления локдаунов, санкций и так далее.
В общем виде модель имела следующий вид:
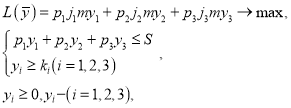
где L(ȳ) = p 1 j 1 my 1 + p 2 j 2 my 2 + p 3 j 3 my 3 → max — целевая функция — прибыль, полученная от приобретенных акций; p 1 , p 2 , p 3 — рыночная цена акций первого, второго и третьего вида; m — период операции в годах; j 1 , j 2 , j 3 — прогнозируемые доходности ценных бумаг соответствующего типа; y 1 , y 2 , y 3 — объем акций каждого типа, соответственно; p 1 y 1 + p 2 y 2 + p 3 y 3 ⩽ S — бюджетное ограничение, связанное с суммой вложений инвестора; y 1 ⩾ k 1 (i = 1, 2, 3) — ограничение и на количество приобретаемых ценных бумаг; y i ⩾ 0(y i ∈ Z) — дополнительные ограничения из экономического смысла задачи.
Как было сказано в этой модели присутствуют комплексные коэффициенты для оценки рисков, причем необходимо использование методов статистики [3] для решения данной модели, которые связывают цену и доходность приобретенных ценных бумаг корреляционной зависимостью. следует ввести комплексный коэффициент оценки рисков, связанных с этими ситуациями, при этом необходимо еще использование статистических методов, дающих возможность учета корреляционной зависимости между ценой и доходностью ценных бумаг, хотя введение новых коэффициентов усложняет решение модели. Доход от приобретенных ценных бумаг будет случайной величиной. Следовательно, доходность будет случайной величиной, а отклонение от ее прогнозируемого значения можно принять за меру риска [4].
Коэффициент склонности инвестора к риску ( К) является субъективной характеристикой. При росте К и неизменности остальных условий выбираются акции с высоким риском. В психологии чаще всего стремление субъекта к риску меняется от 0 до 40. Если этот показатель более 30, то это рискующий субъект, а от 11 до 29 указывает на среднее стремление к риску, менее 11 — указывает на его осторожность.
При стремлении уменьшить риски, надо для каждого типа акций значение риска сравнить с доходностью:
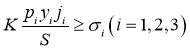
Проще ограничения рисков записать в виде:
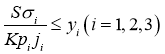
В эту модель были введены нефинансовые риски — описанные новыми параметрами. Риски кризисных ситуаций
ϭ
k
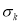
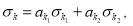
где
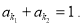
Итоговая математическая модель имеет вид:
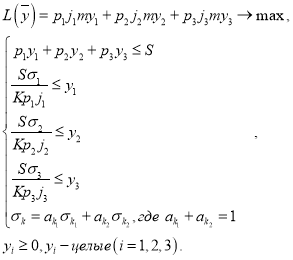
Рассмотрим данные о динамике цен на акции по материалам Investfunds (группа Cbonds) по трем компаниям ОАО «Аптечная сеть 36,6", ОАО «АРМАДА», ОАО «Седьмой Континент».
1) ОАО «Аптечная сеть 36,6". Это холдинговая компания Группы компаний, включающей крупнейшую в России аптечную сеть «36,6» и российского производителя лекарственных средств ОАО «Верофарм». 1168 аптек находятся под управлением Компании. Цена акции во время открытия торгов 142.62 руб.
2) ОАО «АРМАДА». Это российская ИТ-компания, предоставляющая услуги в области информационных технологий. ОАО «АРМАДА» образована путем выделения ИТ-бизнеса из группы компаний РосБизнесКонсалтинг. Портфель решений компании охватывает все области ИТ рынка: разработка ПО, ИТ-услуги, Аппаратное Обеспечение. Клиентская база компании составляет более 700 компаний крупного и среднего бизнеса из различных секторов экономики, а также государственные структуры. В портфеле ИТ-контрактов АРМАДА приблизительно 50 % выручки приходится на коммерческие российские компании, около 40 % на заказы государственных учреждений и 10 % на заказы иностранных клиентов. Цена акции во время открытия торгов 265.03 руб.
3) ОАО «Седьмой Континент». ОАО «Седьмой Континент» является международной розничной торговой сетью, одним из ведущих торговых операторов в России. Компания имеет представительство в Москве и Московской области, в Калининградской области, в Санкт — Петербурге, в Рязани и в Минске, республика Беларусь. Цена на момент открытия торгов 260.88 руб.
Составим математическую модель оптимального формирования портфеля акций этих компаний. Введем обозначения y 1 — количество акций первого вида (ОАО «Аптечная сеть 36,6"), y 2 — количество акций второго вида (ОАО «АРМАДА»), y 3 — количество акций третьего вида (ОАО «Седьмой Континент»). Будем считать, что цена на акции, согласно прогнозу, будет минимальной:
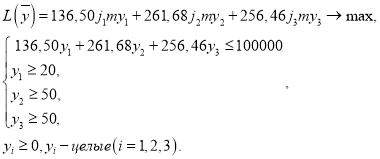
Допустим владелец будет держать акции один год ( m = 1 ), то доходность каждой компании исходя из прогноза, согласно таблицы составит 1) -0,0915, то есть убыток 9,1 %; 2) -0,795, то есть убыток 79,5 %; 3) -0.3217, то есть убыток 32,417 %. При максимальной стоимости по прогнозу:

Ожидаемая доходность через год будет 1) 1,84, то есть 184 %; доход; 2) 0,0845, то есть доход 8,45 %; 3) 0,7837, то есть доход 78,37 %. Как говорилось раньше, недостаток этой модели — произвольное определение ограничений на количество покупаемых ценных бумаг. Данные расчеты подтвердили это.
При сравнении доходности по наилучшему и наихудшему варианту видим, что независимо от наименьшей стоимости наименее убыточны акции ОАО «Аптечная сеть 36,6" и они же имеют наибольшую доходность. А наиболее убыточны и наименее доходны акции ОАО «АРМАДА». Следовательно, долю акций ОАО «Аптечная сеть 36,6" надо увеличить и уменьшить долю ОАО «АРМАДА». Предположение, что надо покупать меньше акций ОАО «Аптечная сеть 36,6", и больше акций ОАО «Седьмой Континент» и ОАО «АРМАДА» оказалось ошибочными.
Допустим, что различия между реальной и ожидаемой доходностью этих компаний составило 0,05, 0,10, 0,15, 0,18, 0,20 соответственно. Предполагая склонность к риску равной 5 (инвестор действует осмотрительно), определяя ограничения по риску и вследствие чего изменяя ограничения по минимальному количеству покупаемых акций, построим более сложную модель в наилучшем случае:

Далее приведены результаты расчетов для последней модели. Для всех видов акций принято одно усредненное значении среднего квадратического отклонения от ожидаемой доходности σ .
Для стоимости акций p 1 = 142,62, p 2 = 266,39 и p 3 = 263,50 определим оптимальный состав портфеля в зависимости от риска (отклонения ожидаемой доходности). Результаты приведены в таблице 1.
Таблица 1
Оптимальный состав портфеля
|
σ |
Количество акций |
L(x) |
||
|
y 1 |
y 2 |
y 3 |
||
|
0,05 |
607 |
45 |
5 |
161334,9 |
|
0,10 |
516 |
89 |
10 |
139477,6 |
|
0,15 |
423 |
134 |
15 |
117117,9 |
|
0,18 |
369 |
160 |
18 |
104152,0 |
|
0,20 |
331 |
178 |
20 |
94998,2 |
Из расчетов видно, что при росте σ и при неизменности остальных постоянных, заметно изменилось количество покупаемых акций. Число более доходный акций ОАО «Аптечная сеть 36,6" уменьшилось с 607 до 331, а число акций ОАО «АРМАДА» и ОАО «Седьмой Континент» увеличилось соответственно с 45 до 178 и с 5 до 20. Сильнее завися от финансового риска, который характеризуется средним отклонением от ожидаемой доходности, о более доходные акции ОАО «Аптечная сеть 36,6", и напротив наименее зависимыми оказались акции других компаний. Максимум целевой функции при увеличении σ уменьшился с 161334,9 до 94998,16 денежных единиц. Прибыль при покупке акций будет равна 61334.9 денежных единиц, при σ = 0,05, -39477,6 денежных единиц, при σ = 0,1, -17117,9 денежных единиц, при σ = 0,15, -4125 денежных единиц, при σ = 0,18. В последнем случае целевая функция равна 94998,16 это означает, что инвестору не выгодно приобретать акции, потому что суммарная прибыль оказалась меньше вложенных средств.
Литература:
- Модель Шарпа — Формирование портфеля ценных бумаг. — Текст: электронный // Учебные материалы онлайн: [сайт]. — URL: https://studwood.net/1449192/finansy/model_sharpa (дата обращения: 01.11.2022).
- Методы анализа социально-экономических процессов в сфере сервиса: сборник научных трудов / Санкт-Петербургский государственный университет сервиса и экономики; редакторы: А. Д. Викторов, О. Ю. Тарасова. — Санкт-Петербург: Санкт-Петербургский государственный университет сервиса и экономики, 2012. — 171 с.
- Лавренов, И. И. Excel сборник примеров и задач. — Москва.: Изд-во «финансы и статистика», 2001. — 336 с.
- Кузнецов, Б. Т. Математические методы и модели исследования операции. — М.: ЮНИТИ-ДАНА, 2005. — 390 с.







