Наличие дефектов в элементах технологического оборудования требует повышенного внимания и исследования влияния дефекта на напряженно-деформированное состояние (НДС) конструкции во избежание выхода из строя при длительном использовании трубопровода [1, 3].
Моделирование напряженно-деформированного состояния (НДС) отвода Ø159х6 на трубопроводе насыщенного водяного пара из пакетов испарителя в барабан котла-утилизатора в условиях эрозионного утонения стенки и определение критической толщины стенки отвода при упругом поведении материала.
Основные геометрические параметры отвода Ø159х6 приняты в соответствии со стандартными параметрами, приведены в таблице 1.
Таблица 1
Геометрические параметры отвода
|
DN, мм |
D, мм |
Т, мм |
F, мм |
R, мм |
B, мм |
Масса, кг |
|
150 |
159 |
6 |
225 |
225 |
305 |
8,1 |
По направлению движения продукта в аварийном трубопроводе к данному отводу посредством сварки присоединены прямолинейные участки № 1.2 и № 1.1 соответственно. Отвод обозначен позицией № 1.3.
С учетом проведенных измерений построена модель участка паропровода по фактическим размерам с учетом эллипсности и минимальных толщин. Минимальная толщина стенки отвода на участке геометрического утонения в зоне возникшего разрушения при моделировании изменялась с шагом 0,6 мм от 0,6 мм до 3,0 мм. Также было рассмотрено НДС при минимальной толщине стенки отвода 5,3 мм. Замеренная эллипсность составила следующие значения по соответствующим диаметрам на участках:
— участок № 1.1: D 1–3 =158,8 мм, D 2–4 =160,8 мм;
— участок № 1.2: D 1–3 =157,8 мм, D 2–4 =160,8 мм;
— участок № 1.3: D 1–3 =158,8 мм, D 2–4 =160,8 мм.
На рисунке 1 представлена модель участка трубопровода.
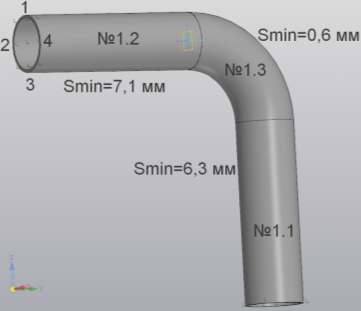
Рис. 1. Модель участка трубопровода
На примере конструкции с утонением стенки, равном 0,6 мм на рисунке 2 приведены фрагменты продольного сечения модели [2]. Утонение выполнено путем плавного удаления части геометрии на внутренней поверхности для имитации эрозионного разрушения поверхности. Наиболее тонкое место принято по внешней образующей в положении угла 30⁰ от нижней кромки отвода.
Геометрические отклонения фактических размеров обуславливают незначительное смещение кромок в зоне сопряжения элементов трубопровода.
На рисунке 2 представлена модель отвода с утонением.

Рис. 2. Модель отвода с утонением 0,6 мм в зоне эрозионного износа
Аналогичным образом были построены модели отводов при утонении стенки в описанной зоне до значений 1,2; 1,8; 2,4 и 3,0 мм, а также модель без износа с фактической толщиной стенки 5,3 мм.
Для численного решения задачи в условиях упругого нагружения необходимо обеспечить закрепление и нагружение модели отвода. В целях снижения влияния зоны закрепления на НДС исследуемого отвода приняты следующие условия закрепления:
— на участке трубопровода № 1.2 свободный конец — жесткое закрепление по осям 0-X и 0-Y;
— на участке трубопровода № 1.1 свободный конец — жесткое закрепление по оси 0-Z.
Модель отвода с участками трубопровода нагружены расчетным внутренним давлением 3,8 МПа.
Для численного моделирования методом конечных элементов модель отвода с примыкающими линейными участками трубопровода была разбита на 4-узловые тетраэдры. Количество таких элементов составило 31650, количество узлов — 11330. Шаг разбиения был принят равным 20, коэффициент сгущения сетки на поверхности Кс=3, коэффициент разряжения сетки в объеме Кр=1,2.
Конечно-элементная модель приведена на рисунке 3.
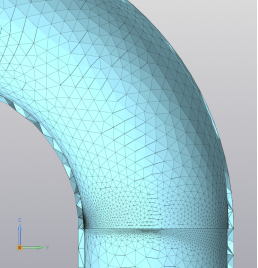
Рис. 3. Конечно-элементная модель участка трубопровода с отводом
При заданных условиях было исследовано напряженно-деформированное состояние участка трубопровода с отводом в упругой постановке. При этом обсчитывалось состояние отвода при разных степенях его эрозионного износа. Общая картина напряженно-деформированного состояния с определением эквивалентных напряжений по Мизесу приведены на рисунке 4.
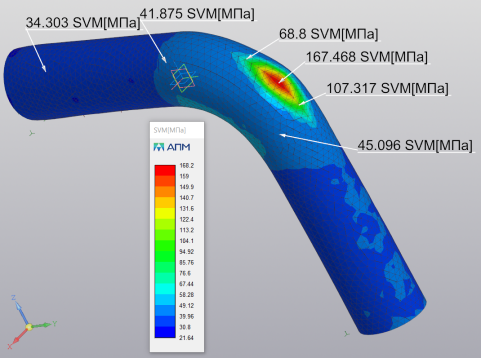
Рис. 4. Распределение эквивалентных напряжений при эрозионном утонении стенки отвода 0,6 мм
Подобным образом были исследованы распределения эквивалентных напряжений без утонения при толщине стенки 1,2 мм, 1,8 мм, 2,4 мм, 3,0 мм, 5,3 мм соответственно.
Таким образом, при каждой степени утонения стенки получены распределения эквивалентных напряжений по поверхности отвода. Обобщая максимальные значения эквивалентных напряжений в зоне утонения построен график данной зависимости, который приведен на рисунке 5.
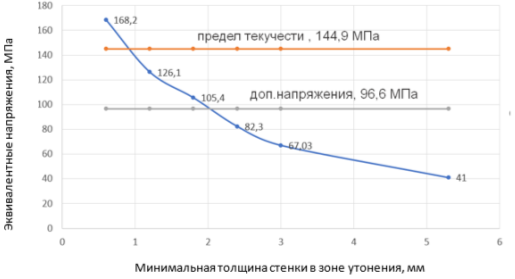
Рис. 5. Зависимость эквивалентных напряжений от минимальной толщины в зоне утонения отвода
Установлено, что чем больше степень эрозионного износа отвода, тем выше эквивалентные напряжения в нем в зоне утонения.
При заданных расчетных условиях (Ррас.=3,8 МПа, Трас.=380⁰С) при остаточной толщине стенки 2 мм в зоне эрозионного износа отвода эквивалентные напряжения достигают значений допускаемых напряжений (96,6 МПа) для стали 20 при расчетной температуре. При утонении стенки до 1 мм величина эквивалентных напряжений достигает значения предела текучести (144,9 МПа) стали 20 при расчетной температуре, происходит пластическое деформирование и разрушение отвода. Для дальнейшего исследования разрушения отвода требуется решение задачи в упругопластической постановке с учетом нелинейности свойств материала.
Литература:
1. Кузеев, И. Р. Трещинообразование в элементах реакторного оборудования / И. Р. Кузеев, А. А. Минниахметова, В. А. Гафарова // Нефтегазовое дело. — 2015. — Т. 13, № 3. — С. 140–145.
2. Гафарова, В. А. Диагностика ресурса конструкций / В. А. Гафарова, М. И. Кузеев, А. П. Терехов // Вестник молодого ученого УГНТУ. — 2016. — № 2. — С. 62–67.
3. Ахтареева, Л. П. Причины и условия распространения трещин при различных режимах нагружения оборудования / Л. П. Ахтареева // Материалы 70-й научно-технической конференции студентов, аспирантов и молодых ученых УГНТУ / УГНТУ. — Уфа, 2019. — Т. 1. — С. 192–193.







