From this thesis, the methods of calculating indefinite integrals of several non-standard functions are presented, and the calculation of these indefinite integrals is directly related to the creation of a mathematical model of some life problems.
Keywords: non-standard functions, integer part of a number, fractional part of a number, signimum function.
Standard functions and methods of calculating indefinite integrals of functions generated by these functions are known to university students from the Mathematical Analysis course. In this thesis, the methods of calculating the indefinite integrals of the functions, which are encountered in the process of creating a mathematical model of several life problems and are called non-standard functions, are presented.
Example 1.
Calculate the following indefinite integral:
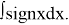
Solution.
To calculate this integral, we use the following property of the signimum function:
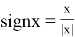
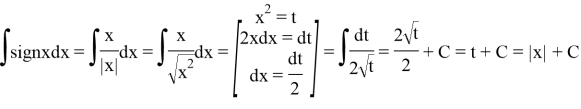
Thus,
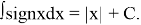
Example 2.
Calculate the following indefinite integral:
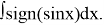
Solution. Let's use the property from Example 1 above:
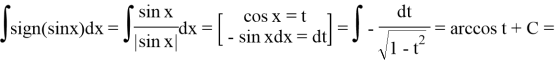
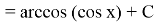
Example 3.
Calculate the following indefinite integral:
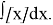
Solution.
The following equations are valid for the function
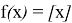
when
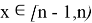
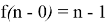
when
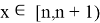
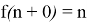
If we define the antiderivative function of the function as
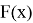
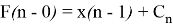
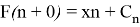
Since the equality
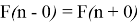
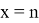
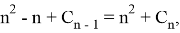
From this equality, we arrive at the following recurrent sequence:

We solve the generated recurrent sequence. To do this, we give a consecutive value to the
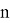
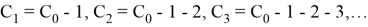
Therefore, the general term of the given recurrent sequence is defined as follows:
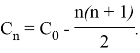
From this, we will have this equality:
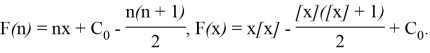
Thus,
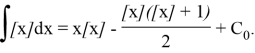
Example 4. Calculate the following indefinite integral:
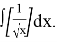
Solution. To calculate this integral, we can first substitute as follows:
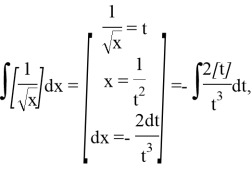
We define the function under the integral as
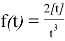
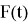
We write this function and its antiderivative function in the following forms, as in the Example 3:
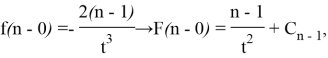
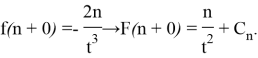
Since the equality
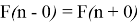
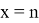
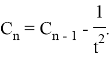
We find the general term of the generated recurrent sequence:
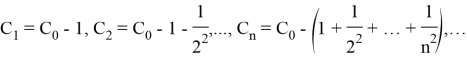
If we take the found general term to the equation where the antiderivative function of the function is found, we will find the indefinite integral of the given function:
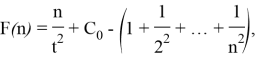
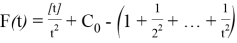
Thus,
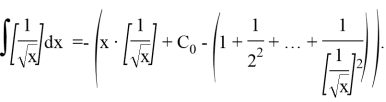
Example 5.
Calculate the following indefinite integral:
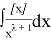
Solution.
The following equations are valid for function
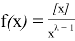
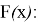
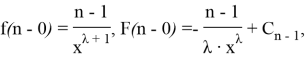
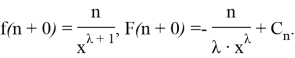
Since the equality
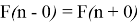
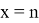
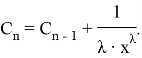
From this we get this equality
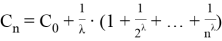
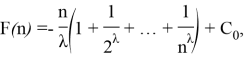
Thus, the indefinite integral of the given function is in the following form:
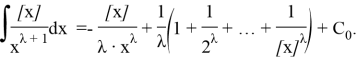
Example 6.
Calculate the following indefinite integral:
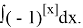
Solution.
The following equations are valid for function
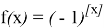
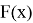
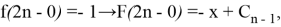
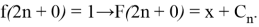
Since the equality
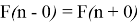
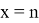
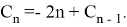
It is easy to find that the general term of this recurrent sequence has the following form:
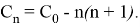
Thus, the indefinite integral of the given function is in the following form:
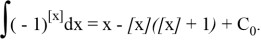
Example 7.
Calculate the following indefinite integral:
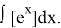
Solution. To calculate this integral, we can first substitute as follows:
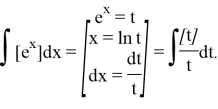
The following equations are valid for function
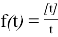
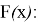
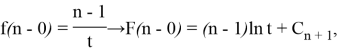
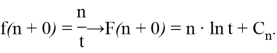
Since the equality
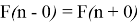
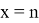
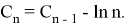
It is easy to find that the general term of this recurrent sequence has the following form:
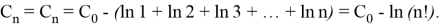
Thus, the indefinite integral of the given function is in the following form:
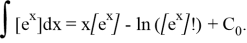
References:
- Alimov Sh., Ashurov R. Matematik tahlil. 1-qism. “Mumtoz so`z”, Toshkent, 2018.
- Демидович Б. П. Сборник задач и упражнений по математическому анализу. Издательство ЧеРо, 13-е издание. 1997, Москва.
- Sa’dullayev A., Mansurov H., Xudoyberganov G. va b. q. Matematik analiz kursidan misol va masalalar to`plami. 1-qism. “O`zbekiston” nashriyoti. Toshkent, 1993.







