Для акустики представляет интерес обработка сигналов, а отдельно — взаимная обработка. Гидроакустические сигналы — это акустические колебания, распространяющиеся в водной среде и несущие информацию о своём источнике, а также используемые для эхолокации объектов, навигации и связи. Они обладают частотными, временными, энергетическими и пространственными характеристиками. В задачах обработки гидроакустических сигналов шумоизлучения объектов входят определения уровня сигнала и уровня помехи, определение отношение сигнал/помеха, что является одним из основных параметров, определяющих помехоустойчивость систем обнаружения и их основных характеристик, таких как вероятность правильного обнаружения и вероятность ложной тревоги. Взаимная обработка сигналов применяется, например, для оценки влияния помех на передачу информации, для устранения взаимных помех, а также для обнаружения и устранения искажений, вызванных этими помехами. Взаимная обработка может быть реализована на основе взаимной корреляции (метод корреляционного анализа).
Анализ — это один из ключевых моментов обработки сигналов. Основная цель анализа — это выявление сходств и различий сигналов посредством сравнений их друг с другом. Существует три основные составляющие анализа сигналов:
1) Измерение числовых параметров сигналов, таких как энергия, средняя мощность, среднеквадратическое значение.
2) Разложение сигнала на элементарные составляющие для их рассмотрения по отдельности либо для сравнения свойств различных сигналов. Такое разложение производится с использованием рядов и интегральных преобразований, важнейшими среди которых являются ряд Фурье и преобразование Фурье.
3) Количественное измерение уровень сходства различных сигналов. Такое измерение производится с применением аппарата корреляционного анализа.
Корреляционный анализ наряду со спектральным играет большую роль в теории сигналов. Его смысл состоит в количественном измерении степени сходства различных сигналов [1].
Корреляционный анализ используется при необходимости оценить временные свойства сигнала без применения спектрального анализа, например, для оценки скорости изменения или длительности сигнала, временной связи (корреляции) одного сигнала с другим.
Корреляционная функция (КФ; английский термин — correlation function, CF) детерминированного сигнала с конечной энергией представляет собой интеграл в бесконечных пределах от произведения двух копий сигнала, сдвинутых друг относительно друга на время
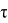
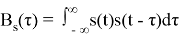
Корреляционная функция показывает степень сходства между сигналом и его сдвинутой копией — чем больше значение корреляционной функции, тем это сходство сильнее.
Взаимная корреляционная функция (ВКФ; английский термин — cross-correlation function, CCF) определяет временную связь двух сигналов во времени. Если сигналы независимы друг от друга, их корреляционная функция равна нулю. Чем шире корреляционная функция, тем большая степень связи двух сигналов друг с другом [2].
Общий вид формулы для ВКФ сохраняется, но под знаком интеграла стоит произведение двух разных сигналов, один из которых задержан на время
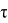
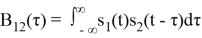
Отличие ВКФ от КФ состоит в том, что КФ показывает степень сходства между сдвинутыми копиями одного и того же сигнала, а ВКФ позволяет измерить аналогичную величину для сдвинутых экземпляров двух разных сигналов.
Таким образом, появилась необходимость реализовать программу для автоматизации построения графика взаимной корреляционной функции двух сигналов с целью последующего их анализа.
Метод расчета (получения оценок) взаимных корреляционных функций основан на соотношении, представляющем свертку двух сигналов в виде обратного преобразования Фурье комплексно-сопряженного произведения их Фурье образов. Для получения оценки выполняется следующая последовательность действий:
Из двух реализаций сигнала, представленных последовательностями отсчетов
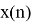
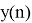
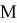
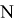
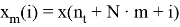
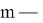
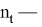
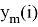
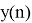
Последовательности дополняются
Для отрезков вычисляются преобразования Фурье с использованием алгоритма БПФ.
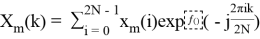
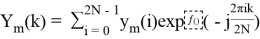
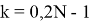
Для каждого результата БПФ
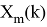
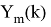
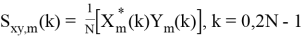
Выполняется усреднение по
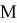
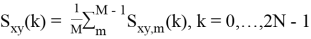
Выполняется обратное преобразование Фурье последовательности
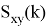
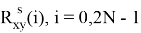
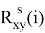
Рассчитывается нормированная оценка для положительных сдвигов взаимно взаимной корреляционной функции
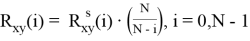
Рассчитывается нормированная оценка для отрицательных сдвигов взаимно взаимной корреляционной функции
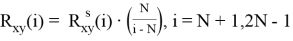
Параметры алгоритма расчета взаимной корреляционной функции полностью аналогичны параметрам расчета корреляционной функции
Параметрами алгоритма расчета являются:
1) длина участка реализации (число отсчетов), используемая для расчета не усредненной оценки спектра;
2) число усреднений спектров при формировании корреляционной функции.
Для примера были взяты два гармонических сигнала с разными амплитудами:
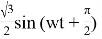
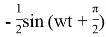
Были рассчитаны спектры двух сигналов и их взаимный спектр (рис.1), а затем их взаимная корреляционная функция (рис. 1).
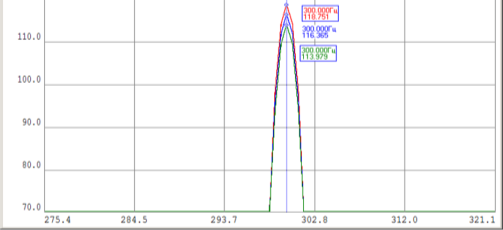
Рис. 1. Взаимный спектр первой пары сигналов и спектры двух сигналов
На рисунке 1 красная линия — спектр сигнала
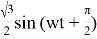
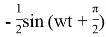
Поскольку за исключением амплитуд сигналы абсолютно одинаковые, уровень взаимного спектра на частоте 300 Гц определяется произведением амплитуд этих сигналов.
На рисунке 2 красная линия — КФ сигнала
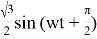
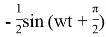
Амплитуда ВКФ в данном случае также определяется произведением амплитуд используемых сигналов.
Как видно из графика, ВКФ имеет достаточно большую ширину, что позволяет судить нам о сильной корреляции используемых в анализе сигналов.
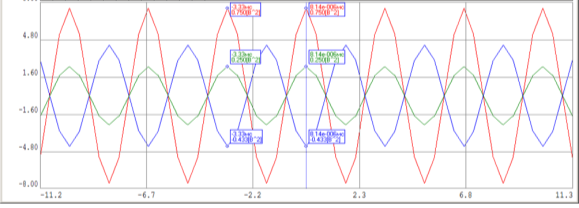
Рис. 2. ВКФ первой пары сигналов и КФ двух сигналов
Затем для сравнения были использованы хаотичные сигналы (шум).
Сначала были построены спектры двух сигналов и их взаимный спектр (рис. 3), а затем их взаимная корреляционная функция в разных масштабах (рис. 4 и рис. 5).
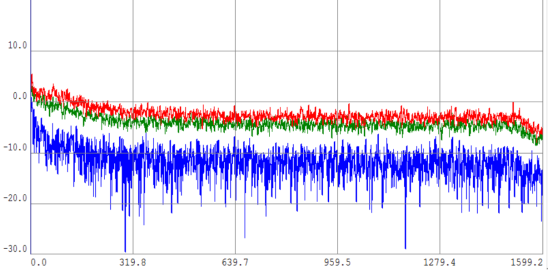
Рис. 3. Взаимный спектр второй пары сигналов и спектры двух сигналов
На рисунке 3 красным и зеленым цветом обозначены спектры сигналов, а синим цветом — их взаимный спектр.
На рисунках 4 и 5 аналогично красным и зеленым цветом обозначены КФ сигналов, а синим цветом — их ВКФ.
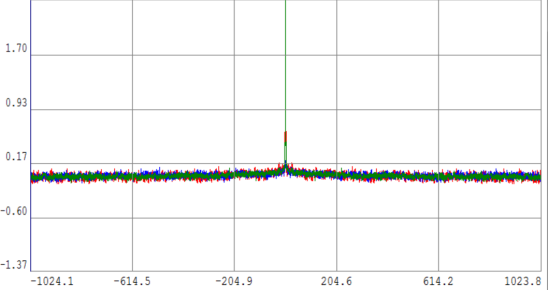
Рис. 4. ВКФ второй пары сигналов и КФ двух сигналов
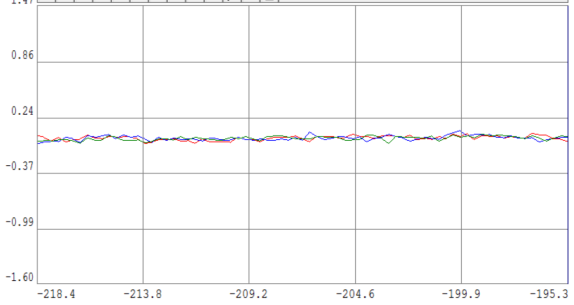
Рис. 5. ВКФ второй пары сигналов и КФ двух сигналов
Из графиков видно, что ВКФ сигналов стремится к нулю, следовательно, вторая пара сигналов некоррелирована.
ВКФ часто используется при обработке сигналов, например, для распознавания отраженного от объекта локационного сигнала (радаров, сонаров) в условиях помех. Кроме того, ВКФ используется для восстановления сигналов из их кодовых и временных копий. Примером может служить восстановление сигнала с помехами, когда информация искажена или потеряна.
Таким образом, взаимная обработка играет значительную роль в анализе сигналов. При создании акустического профиля исправного оборудования и сравнении его с текущим профилем с помощью взаимной обработки на ранних стадиях можно обнаружить неисправность и принять соответствующие меры, что может быть использовано для диагностики плавсредств. В дальнейшем планируется разработка отдельного программного обеспечения для диагностики плавсредств, разработка алгоритмов, интерфейса и программ вывода результатов.
Литература:
- Сергиенко, А. Б. Цифровая обработка сигналов / А. Б. Сергиенко. — СПб.: Питер. — 604 c.
2. Полный курс основы аналоговой схемотехники. Лекции. // МИЭМ. Автор: Андреевская Т. М. — 2005 г. — 108 c.







