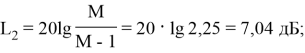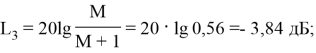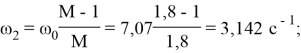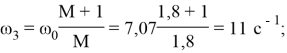Метод желаемой логарифмической частотной характеристики для синтеза регулятора в системе управления



В статье рассматривается метод синтеза регулятора для заданного объекта управления, и его моделирование с помощью встроенных приложений в MATLAB.

Ключевые слова: желаемая логарифмическая частотная характеристика, синтез регулятора.

Введение

При проектировании систем автоматического управления (САУ) главной задачей является синтез, т. е. создание новой системы путём определения всех свойств и качественных показателей системы.

Задача синтеза заключается в выборе структурной схемы и технических средств ее реализации, при котором обеспечиваются требуемые показатели системы.

В настоящее время существует большой спектр методов и алгоритмов для решения задачи синтеза, например корневой метод — [1, c.79]. В этой статье будет рассмотрен один из методов, использующий логарифмические частотные характеристики — метод желаемой логарифмической амплитудной частотной характеристики (ЖЛЧХ). Т. к. этот метод наиболее удобный для синтеза и может выполняться без дополнительной вычислительной работы.

Метод ЖЛЧХ заключается в построении ЛАЧХ и ЛФЧХ по заданному объекту и критериям качества для проектируемой САУ. Процесс построение ЖЛАЧХ обычно разбивается на несколько этапов: построение на низких частотах (НЧ), средних частотах (СЧ) и высоких частотах (ВЧ), определение запретной зоны для ЛФЧХ и по необходимости корректировка ЛАЧХ, чтобы система удовлетворяла заданным требованиям.

Построение НЧ области начинается с определения задающих воздействий, в зависимости от типа воздействия определяется допустимое значение установившейся ошибки и необходимая добротность системы. И в результате определяется прямая на участке НЧ, выше которой должная проходить ЖЛАЧХ.

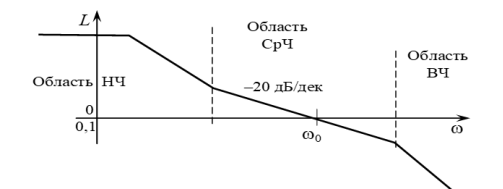
Рис. 1. Типовые области для метода ЖЛЧХ

Построение СЧ области определяется временем переходного процесса, перерегулированием и показателем колебательности, т. е. , по этим параметра определяются частоты, через которые будет дальше проходить ЖЛАЧХ. Затем участок СЧ соприкасается с участком НЧ.

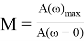
В области ВЧ ЖЛАЧХ проводится либо параллельно ЛАЧХ, либо с большим наклоном, в зависимости от астатизма объекта управления.

Запретная зона ЛФЧХ определяется по показателю колебательности из условия устойчивости системы — [2, c. 350].

Пример синтеза регулятора для заданного объекта управления

Требуется для заданной передаточной функции объекта определить методом ЖЛЧХ передаточную функцию регулятора, при заданных требованиях к качеству системы автоматического управления (САУ):

передаточная функцию объекта

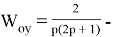
Требования к качеству САУ:

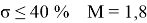
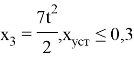
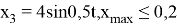
где -время регулирования, с, -перерегулирование, %, -входное задающее воздействие,

-установившаяся ошибка, -максимальное значение ошибки, М — показатель колебательности.

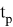
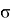
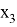
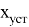
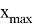
Построение ЖЛАЧХ на низких частотах

В нашем случае входное воздействие имеет вид: , а объект управления имеет астатизм второго порядка — [3, c.34].

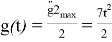
Для воспроизведения такого сигнала передаточная функция должна иметь не менее двух интегрирующих звеньев.

.

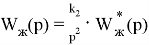
Из этого условия определяется необходимая добротность системы по ускорению:

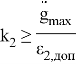
Значит при заданном ускорении входного воздействия, ЖЛАЧХ должна проходить не ниже прямой (рис. 1)

При запасе в 3 дБ:

.

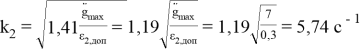
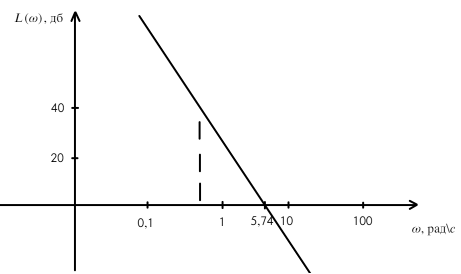
Рис. 2. ЖЛАЧХ в области НЧ для системы с астатизмом второго порядка

Построение ЖЛАЧХ на средних и высоких частотах

Находим частоту единичного усиления среднечастотной части ЖЛАЧХ

.

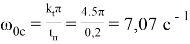
Определяем по графику (рис. 2) для  = 40 %, М = 1,8.

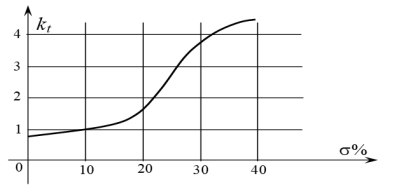
Рис. 3. Зависимость коэффициента kt от перерегулирования

Проверяем условие

,

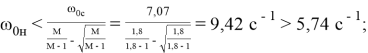
Граничные значения модуля | W _ж ( j )| для участка с наклоном –20 дБ/дек, проходящего через  _0с :

	lg(2,25)=0,35;
	lg(0,64)=–0,19;

В области высоких частот ЖЛАЧХ проводится либо параллельно ЛАЧХ неизменной части, либо с наклоном в -20 дБ/дек от суммарного наклона ЛАЧХ объекта управления. Частота сопряжения с областью средних частот . Наклон ЛАЧХ объекта управления составляет -40 дБ/дек. Следовательно, наклон ЖЛАЧХ на высоких частотах следует выбрать -60 дБ/дек.

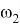
Объединяем НЧ, СЧ и ВЧ части ЖЛАЧХ (рис. 4).

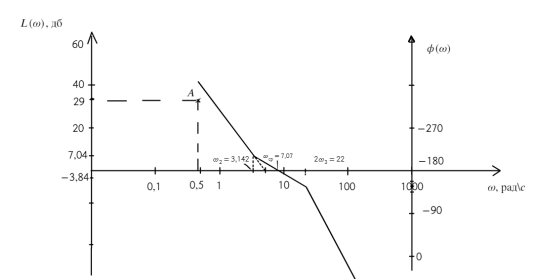
Рис. 4. ЖЛАЧХ в области НЧ-СЧ-ВЧ

Построение ЛФЧХ и запретной зоны

Желаемая передаточная функция определяется по формуле:

, тогда в нашем случае

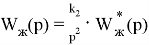
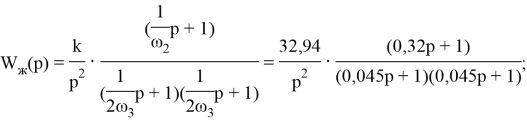
Желаемая передаточная состоит из двойного интегратора, двух апериодических звеньев и одного идеального дифферинцирующего звена.

Запретная зона строится следующим способом:

1. На оси ординат откладываются амплитуды и .

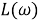
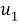
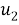
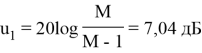
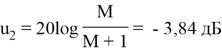
2. На отрезке , как на диаметре, строится полуокружность. На оси откладывается величина

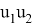
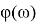
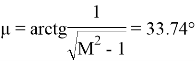
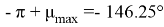
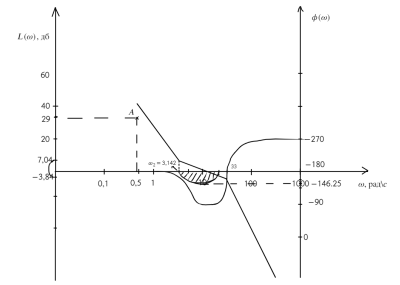
Рис. 5. ЖЛАЧХ в области НЧ-СЧ-ВЧ и запретная зона для ЛФЧХ

Моделирование в MATLAB для проверки параметров переходного процесса

Соберём нашу систему в Simulink с обратной связью:

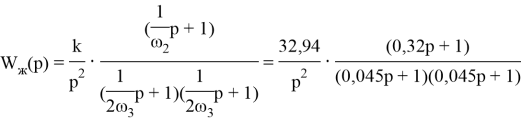
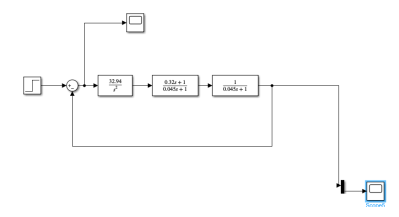
Рис. 6. Спроектированная САУ в Simulink

Проверим, удовлетворяет наша САУ заданным требованиям:

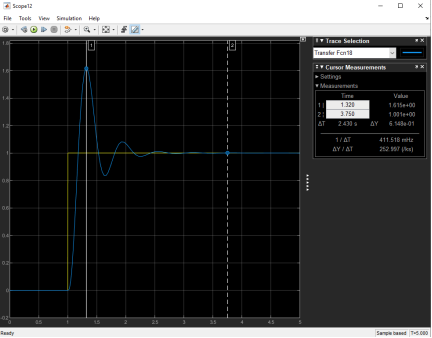
Рис. 7. Переходной процесс

По переходному процессу видно, что наша система на удовлетворяет требованию (коэффициент перерегулирования слишком большой). Немного скорректируем ЖЛАЧХ:

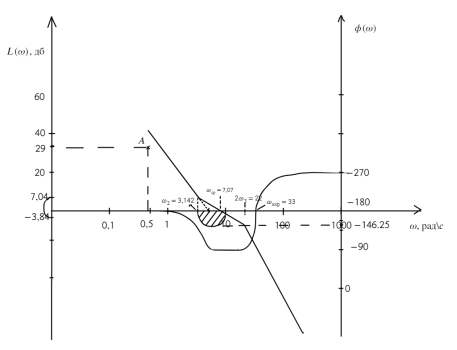
Рис. 8. Скорректированная ЖЛАЧХ

Соберём скорректированную ЖЛАЧХ и проверим параметры системы:

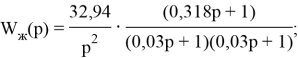
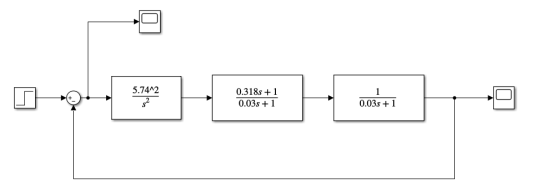
Рис. 9. Скорректированная САУ

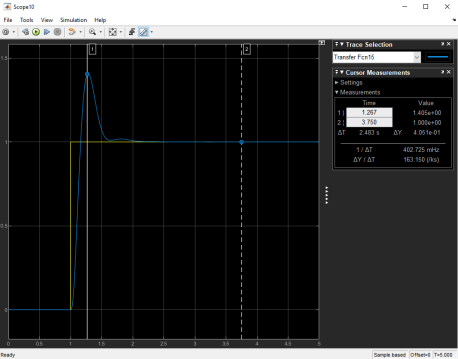
Рис. 10. Переходной процесс скорректированной САУ

По полученным параметрам, видно, что наша скорректированная САУ удовлетворяет требования задания.

Заключение

В результате проведенных в данной статье исследований можно сделать вывод, что метод желаемой логарифмической характеристики является применимым при синтезе регуляторов с заданным объектом управления. Поэтому этот метод следует использовать для определения параметров регулятора, т. к. метод очень наглядно показывает все этапы построения ЖЛАЧХ, позволяет сократить время синтеза и поддерживает внесение корректировок.

Литература:

1. В. Л. Земляков Основы автоматического управления, 2017. — 103 с

2. Теория систем автоматического регулирования. Издание третье, исправленное. Бесекерский В. А., Попов Е. П., 1975–768 с

3. Лазарева Т. Я., Мартемьянов Ю. Ф. Основы теории автоматического управления, 2004–352 с.