В статье рассматриваются методы решения задач оптимального управления с точки зрения применимости отдельных методов синтеза оптимальных САУ в зависимости от структуры и характеристик системы.
Ключевые слова: оптимальные САУ, классификационные признаки оптимальных САУ, методы синтеза и анализа.
Задача оптимального управления включает в себя цель управления, управляемый объект, измерительную систему и вычислительное устройство, осуществляющее расчет оптимального управления, которое находит связи,
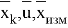
Решение задач оптимального управления предполагает выбор критерия оптимальности, который формирует цель управления, например, достижение определенного значения скорости трактора при автоматическом управлении ходоуменьшителем, минимизация времени регулирования, оптимизация тепловых потерь и т. д. При этом, необходимо учитывать ограничения — так, при минимизации времени регулирования, должны быть в допустимых пределах другие показатели качества переходного процесса. При этом, оценка свойств системы должна быть объективной, формализованной.
В целом, среди практических задач синтеза оптимального управления выделяются следующие: определение оптимальных значений параметров и синтез структуры и параметров регулятора при заданных параметрах и структуры объекта управления.
Решение задач определения параметров возможно различными аналитическими методами при минимизации интегральных оценок, а также с помощью моделирования, в том числе в Matlab, Scilab, Winmass, программный комплекс ТАУ, система компьютерной алгебры Maxima и др. Решение задач второго типа основано на использовании специальных методов: методы классического вариационного исчисления, принципа максимума Понтрягина и др, которые также могут быть успешно реализованы в одной из программ моделирования и/или расчета. Например, для синтеза оптимальных систем при случайных сигналах используются методы Винера, также вариационные и частотные методы. В современных условиях, достаточно актуально развитие адаптивных САУ, в которых неопределенность, в том числе, связанная с не стационарностью объекта, играет ключевую роль при выборе метода синтеза и обеспечения управления. Так, при формализации критерия качества, требуется определить законы изменения настраиваемых параметров. Данная задача связана с синтезом наблюдателей, также в ряде учебных пособий отмечаются возможности применения градиентных методов для данной цели [2,3]. Таким образом, проектирование оптимальных адаптивных САУ предполагает изменение критерия качества и вычисление параметров регулятора, что требует синтеза наблюдателя и сопровождается другими особенностями, связанными с адаптивным управлением [2,5].
При этом, практически все математические постановки задачи оптимального управления сводятся к следующим [5]: достижение максимального быстродействия, управление конечным состоянием, задача управления по минимуму интеграла, которые в свою очередь возможно преобразовать, например, с помощью инвариантного вложения, в задачу оптимизации по отношению к координатам или переменным состояния объекта.
Рис 1. иллюстрирует классификацию оптимальных САУ, которая основана на анализе литературы [1,2,3,4,5] и построена на следующих признаках: оптимизируемые показатели, характер переходных процессов, протекающих в системе, тип дифференциальных уравнений, описывающих систему, характер критерия оптимальности.

Рис. 1. Классификация оптимальных САУ
Равномерно оптимальные — это наилучшие системы в каждом отдельном случае, то есть при каждом проведённом эксперименте, статистически оптимальные системы — наилучшие при усреднении многих экспериментов, минимаксно-оптимальные системы, дающие наилучший результат в наихудших условиях. С точки зрения синтеза, также важно детерминированная система или стохастическая, дискретная или непрерывная.
Так, критерий оптимальности может представлять собой технический или технико-экономический критерий, математическое выражение которого является функцией или функционалом координат процесса и управляющих воздействий. Требования к системе, как правило, противоречивы. В управлении техническими системами, наиболее распространенными являются различные интегральные критерии. Определяющим является показатель точности, который выражается через характеристики, описывающие стохастический характер реальных условий взаимодействия объекта и среды и зависящие от управления.
На данный момент в вариационном исчислении существует три задачи, выражающие критерий оптимальности — это задача Лагранжа, Больца, Маера. Задача Лагранжа является наиболее общей, однако, данные задачи взаимозаменяемы с точки зрения математических операций.
Основные методы, используемые в теории оптимизации, следующие: классическое вариационное исчисление, принцип максимума Понтрягина, динамическое программирование Беллмана, алгоритмы Винера-Колмогорова и Калмана-Бьюси, функциональный анализ, метрический анализ.
Для решения задач оптимального управления используют косвенные (аналитические) методы, а также прямые (численные)методы оптимизации. Прямые методы оптимизации — это методы математического (линейного) программирования, такие как симплекс-метод.
Косвенные методы оптимизации включают в себя методы дифференциального и интегрального исчисления, классическое вариационное исчисление, принцип максимума Понтрягина и метод динамического программирования Беллмана [3].
Для косвенных методов оптимизации ключевым является определение вида оптимальной функции и её структуры на основе необходимых условий оптимальности.
Таким образом, теория оптимизации и математический аппарат, применяемый в методах решения задач оптимального управления предполагает формализацию цели и ограничений для каждой задачи. Выбор критерия оптимальности, как единого показателя проектирования, способствует структурированию и формированию определенного алгоритма синтеза.
В целом, основные этапы построения оптимальных систем состоят в следующем [5]: составление номинальной модели, моделирование САУ, формирование критерия оптимальности, определение оптимальных управляющих воздействий, синтез регулятора.
Так, принцип максимума Понтрягина [1,2,5] позволяет создать САУ оптимальную по быстродействию, при этом, используя данный метод и имея дополнительную задачу, например, оптимизация тепловых потерь, появляется ограничение по оптимальному току, которое замедляет время регулирования. Таким образом, задача проектирования оптимальной САУ — это задача синтеза. Так, для детерминированных и стохастических систем применяется рассмотренная методология, но с некоторыми изменениями. Говоря о непрерывных детерминированных системах, для нахождения оптимального программного управления применяется принцип максимума, при наличии полной обратной связи — уравнение Беллмана. Синтез детерминированной оптимальной САУ с неполной обратной связью предполагает нахождение и применение синтезирующей функции. Предполагается, что при управлении используется информация только о времени
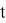
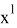
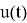
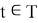
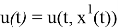
![Задача синтеза детерминированной оптимальной САУ с неполной обратной связью [4, c. 389]](https://moluch.ru/blmcbn/98183/98183.008.png)
Рис. 2. Задача синтеза детерминированной оптимальной САУ с неполной обратной связью [4, c. 389]
Для стохастических непрерывных САУ существует стохастический принцип Максимума, для систем совместного оценивания и управления также предполагается синтез наблюдателя [1,2,3,4]. При решении практических задач часто встречаются случаи, когда часть переменных вектора состояния оказываются неизмеримыми. Если имеется математическая модель системы, то можно вычислить ее состояние по наблюдаемым входам и выходам. Восстановление вектора состояния
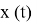
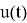
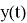
![Структура САУ с накоплением информации о состоянии [4]](https://moluch.ru/blmcbn/98183/98183.011.png)
Рис. 3. Структура САУ с накоплением информации о состоянии [4]
Синтез оптимальных дискретных стохастических систем основан на уравнениях фильтра Калмана для дискретных линейных систем, обеспечивающего нахождение оптимальной оценки вектора состояния модели объекта управления с минимальной нормой ковариационной матрицы ошибки оценивания и на соотношениях определения оптимального управленяи линейной дискретной детерминированной системы при полной информации о векторе состояния [1,4].
Таким образом синтез оптимальных САУ зависит от структуры и характеристик системы. Методы проектирования регуляторов, разработанные для малых областей фазового пространства (вблизи траекторий, соответствующих номинальным режимам), являются неприемлемыми применительно к большим областям фазового пространства в случае нелинейных систем [5]. На практике, существует несколько основных проблем, которые решаются, но требуют определенного внимания при синтезе САУ.
- Формирование значимого на языке математике критерия качества из различных требований проектирования c учетом возможной чувствительности критерия качества к ошибочным предположениям для адаптивных систем, многосвязных объектов и др. [1,5];
- Для нелинейных оптимальных адаптивных систем, актуальна задача упрощения расчета алгоритма управления.
- Синтез оптимальных цифровых регуляторов и методика перехода от непрерывной системы к цифровой.
Литература:
1. Афанасьев В. Н. Математическая теория конструирования систем управления: Учеб. для вузов. / В. Н. Афанасьев, В. Б. Колмановский, В. Р. Носов. — з-е изд., испр. И доп. — М.: Высш. Шк., 2003. — 614 с.
2. Деменков Н. П. Вычислительные методы решения задач оптимального управления на основе принципа максимума Понтрягина: учебное пособие / Н. П. Деменков. — Москва: Издательство МГТУ им. Н. Э. Баумана, 2015. — 75с.
3. Деменков Н. П., Микрин Е. А. Управление в технических системах: учебник / Н. П. Деменков, Е. А. Микрин. — Москва: Издательство МГТУ им. Н. Э. Баумана, 2017. -452с.
4. Пантелеев А. В. Теория управления в примерах и задачах: Учеб. Пособие / А. В. Пантелеев, А. С. Бортаковский. — М.: Высш. Шк., 2003. — 583 с.
5. Шурыгин Ю. А., Карпов А. Г. Современные проблемы теории управления. — Томск: Изд-во Том. Ун-та, 2017. — 80с.







