Мақалада комбинаторика тақырыбы бойынша оқушыларды олимпиадаға дайындауға арналған тапсырмалар түрлері берілген. Комбинаториканың классикалық мәселесі қайталанбайтын комбинациялар саны туралы мәселе болып табылады, оның мазмұны мына сұрақпен көрсетілуі мүмкін: m әртүрлі n нысанның ішінен қанша тәсілмен таңдауға болады? Комбинаторика — бұл кейбір дискретті объектілер жиынтығынан жасалуы мүмкін әртүрлі комбинацияларды санау. Олимпиада математикасының бұл бөлімі дерлік ең классикалық болып табылады. Дегенмен, мектептерде, тіпті математикалық мектептерде де олар өте аз.Мақалада комбинаториканың олимпиадалық есептері толық шешімімен берілген, ол студенттерге өздігінен дайындалуда қажет.
Түйінді сөздер: комбинаторика, олимпиада, орналастыру, алмастыру, терулер, конфигурациялар.
В статье представлены виды заданий для подготовки учащихся к олимпиаде по теме комбинаторика. Классическая проблема комбинаторики — это вопрос о количестве повторяющихся комбинаций, содержание которых может быть выражено следующим вопросом: сколькими способами можно выбрать m из n различных предметов? Комбинаторика — это подсчет различных комбинаций, которые могут быть созданы из некоторого дискретного набора объектов. Этот раздел олимпийской математики является почти самым классическим. Однако в школах, даже в математических, их очень мало. В статье представлены олимпиадные задачи по комбинаторике с полным решением, что необходимо студентам для самостоятельной подготовки.
Ключевые слова: комбинаторика, олимпиада, размещение, подстановка, циферблаты, конфигурации.
Менің мақаламның тақырыбы «Комбинаторика бойынша олимпиада есептерін шешу». Бұл мақаламда оқушылардың осы тақырып бойынша олимпиадаға дайыналуға бастама есептері жинақтақталған. Ғылым мен техниканың даму дәрежесі мектептерге математиканы оқытуды қазіргі заман талаптарына сәйкес жүргізуді талап етеді. Ерекше талантты оқушыларды анықтау қазіргі заманның маңызды проблемалары мен әдістемелеріне,оның соңғы жылдардағы жетістіктері мен нәтижесіне жастардың қалың көпшілігін тарту мақсатында соңғы жылдары Республика мектептерінде әр түрлі деңгейдегі математикалық олимпиадалар өткізу дәстүрге айналды. Мұндай жарыстар алдымен мектепте,ауданда,облыста,республикада одан кейін Халықаралық деңгейде өткізіліп келеді. Әр түрлі деңгейдегі математикалық олимпадаларды ұйымдастыру мәселелері мен оны өткізу әдістемесі қазіргі кездегі өзекті мәселенің бірі болып табылады. Олимпиадалық есептер шығарудың математиканы оқып үйренуде алатын орны ерекше.
«Комбинаторика» (кейде комбинаторлық талдау деп те аталады) — берілген ережелерге сәйкес кейбір (көбінесе ақырлы) жиынның элементтерін таңдауға және орналастыруға байланысты есептерді шешуге арналған математика бөлімі. Әрбір осындай ереже бастапқы жиынның элементтерінен белгілі бір таңдауды анықтайды, ол комбинаторлық конфигурация деп аталады. Комбинаторлық конфигурациялардың қарапайым мысалдары: ауыстырулар,комбинациялар және орналастырулар болып табылады. Комбинаториканың типтік тапсырмалары: берілген ережелерге сәйкес келетін комбинаторлық конфигурациялардың санын анықтаңыз (атап айтқанда, олардың бар екенін дәлелдеңіз немесе жоққа шығарыңыз).
— Олардың толық құрылысы үшін іс жүзінде қолайлы алгоритмді табыңыз.
— Комбинаторлық конфигурациялардың берілген класының қасиеттерін анықтаңыз. Комбинаторика математиканың көптеген басқа салаларымен — алгебра, геометрия, ықти-малдықтар теориясы, сандар теориясы және т. б. тығыз байланысты. Ол білімнің әртүрлі салаларында (мысалы, генетикада, информатикада, статистикада, статистикалық физикада лингвистикада) қолданылады.«Комбинаторика» терминін математикалық қолданысқа Лейбниц енгізді, ол 1666 жылы «Комбинаторлық өнер туралы дискурстар» еңбегін жариялады.
Жалпы комбинаторика тақырыбының есептері 5-сыныптан бастап енгізіле бастайды. Ал жоғары сыныптарда 9-сыныптан бастап комбинаторика тақырыбы толығымен түсіндіріледі.Енді осы тақырыпта оқушыларды олимпиадаға дайындауға бастама ретінде мына есеп-терді қарастыруға болады.
Мысыал 1. Цифрларының қосындысы 4-тен кіші 4 таңбалы неше сан бар?
Шешімі: Мұнда белгілейтін ештеңе жоқ — біз қазірдің өзінде сандармен айналысамыз. Цифрларының қосындысы 1, 2 немесе 3 болатын барлық төрт таңбалы сандарды өсу ретімен жазу ғана қалады:
1000, 1001, 1002, 1010, 1011, 1020, 1100, 1101, 1110, 1200, 2000, 2001, 2010, 2100, 3000.
Барлығы 15 сан бар.Опциялар өте көп болуы мүмкін, бірақ кейбір жағдайларда мәселені шешудің ең жылдам жолы — саналы түрде ұйымдастырылған санау.
Тапсырма 2. «Ыдыс аяқ» дүкенінде 5 түрлі кесе және 3 түрлі тәрелке бар.Кесе мен табақшаны неше тәсілмен сатып алуға болады?
Шешуі: Кесе таңдап алайық.Ол үшін жиынтықтағы үш табақшаның кез келгенін таңдай аласыз.Сондықтан таңдалған кеседен тұратын 3 түрлі жиынтық бар.Бар болғаны 5 кесе болғандықтан, әртүрлі жиынтықтардың саны 15 (15= 5*3)
Тапсырма 3. «Ыдыс аяқ» дүкенінде тағы 4 шай қасық бар. Тостағандар, табақшалар мен қасықтар жиынтығын қанша жолмен сатып алуға болады?
Шешуі: Алдыңғы есептің 15 жиынының кез келгенін таңдаймыз.Оны қасықпен төрт түрлі жолмен толықтыруға болады.Сондықтан мүмкін болатын жиындардың жалпы саны 60 (15*4=5*3*4)
Тапсырма 4. Ғажайыптар елінде үш қала бар: А, В және С.А қаласынан В қаласына дейін 6 жол, В қаласынан С қаласына дейін 4 жол бар (1-сурет).А-дан C дейін неше жолмен баруға болады.? Шешуі: 24=6*4
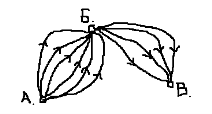
Сурет 1
Өзіндік жұмысқа арналған тапсырмалар:
- Үшбұрыштың әр жағына 5 нүкте боялған. Осы нүктелерден барлығы неше үшбұрыш құрауға болады?
- Күн жүйесінің 9 планетасы арасында ғарыштық байланыс енгізілді. Ракеталар келесі мынадай бағыт бойынша ұшады. Жер-Меркурий, Плутон-Венера, Жер-Плутон, Плутон-Меркурий, Меркурий-Венера, Уран-Нептун, Нептун-Сатурн, Сатурн-Юпитер, Юпитер- Марс, Марс-Уран. Жерден Марсқа ұшып баруға болада ма?
- Бірінші суретте көрсетілген бастапқы позициядан рыцарлармен бірнеше қимыл жасағаннан кейін оларды екінші суретте көрсетілгендей ретке келтіруге болады ма?
- Сан елінде 1,2,3,4,5,6,7,8,9 атаулары бар 9 қала бар. Саяхатшы осы қалалардың атауларының цифрларынан тұратын екі таңбалы сан 3-ке бөлінетін болса ғана, екі қаланы әуе компаниясы байланыстыратынын біледі. 1 қаладан 9 қалаға жетуге бола ма?
Қортынды : Комбинаторика — бұл опцияларды санау. Ол үшін мектеп оқушыларына қосынды мен көбейтіндінің ережелерін, сондай-ақ тапсырмаларда тану және классикалық комбинаторлық объектілерді нұсқаларды — ауыстыруларды, комбинацияларды, орналастыруларды (қайталаусыз және қайталаумен) есептеуге үйрету қажет. Эйлер-Венн шеңберлерін, ағаштарды, диграфтарды, Паскаль үшбұрышын, Ньютон биномын, Рэмси теориясын, каталан сандарын және т. б. Осындай типті есептер оқушыны комбинаторика тақырыбы бойынша олимпиадауға дайындалуға үлкен септігін тигізеді.
Әдебиет:
- «Ленинградские математические кружки: пособие для внекласной работы». С. А. Генкин, И. В. Итенбург, Д. В. Фомин:Киров, издательство АСА, 1994.-18 ст.
- А.Шахмейстер. Комбинаторика, статистика, вероятность, 2012,-544 с.
- https://studbooks.net/2558224/matematika_himiya_fizika/elementy_kombinatoriki
- «Задачи по комбинаторике»/ Н. Я. Виленкин.2015,-328ст.
- Алимов А. Ш., Колягин Ю. М., Ткачева М. В. и др. Алгебра и начала математического анализа. 10–11 классы. Базовый и углубленный уровни / Учебник. — 3-е изд. — М.: Просвещение, 2016,-385ст.
- Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике / М. — «Высшая школа», 2004,-398.







