В статье рассмотрен пример полносвязной сети, для которой составлена математическая модель расчета оптимального прохождения трафика по каналам связи контурным методом.
Ключевые слова: математическая модель, полносвязная сеть.
Определение оптимальности распределения трафика, который идет от источника к приемнику, в сетях связи позволяет нам снизить количество теряемой информации, а значит повышает эффективность использования данной сети. Управление трафиком охватывает задачу анализа, оптимизации и синтеза телекоммуникационных сетей, что ведет к необходимости получить математическую модель сети, которая описывается набором линейно-независимых переменных [1]. Математическое моделирование является мощным и эффективным инструментом исследования разнообразных объектов, систем и процессов в различных областях. Решение задачи управления трафиком является одной из ключевых задач телекоммуникационной индустрии [2]. Решение этой задачи позволяет снизить потери трафика, следовательно, повысить качество передаваемой информации. При постоянно возрастающем входном трафике, расширении границ пользователей и количестве предоставляемых им услуг особое значение имеет информационная эффективность информационной сети, заключающаяся в своевременном и без потерь доведении большого количества информации до адресатов. Выяснение оптимального распределения трафика позволит снизить потери, которые происходят на каждом из узлов. Сеть можно рассматривать как совокупность геометрических объектов в пространстве, размерность которого определяется топологией сети [3]. Такой подход облегчает получение математической модели для расчетов.
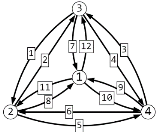
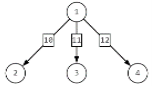
Пусть имеется некоторая полносвязная сеть, представленная в виде направленного графа, для которой необходимо определить прохождение трафика (рис. 1). Предполагаем, что узел 1 является источником и приемником одновременно. Поскольку сумма потоков, которые поступают в сеть и выходят из неё равны между собой, то это эквивалентно объединению рёбер истоков и стоков между собой. Так как количество контурных интенсивностей равно количеству хорд, для их поиска необходимо определить дерево данного графа (рис 2).
|
Рис. 1. Пример некоторой сети, представленной в виде направленного графа. |
Рис. 2. Дерево рассмотренного графа |
Из имеющегося дерева можно сделать вывод, что имеется 3 ветви 10, 11, 12, что можно определить, как 3 источника потока трафика. Остальные ребра графа являются хордами. Поскольку каждый источник, генерирующий трафик, является независимым от других источников, то поток в каждом ребре, создаваемый i-м источником, будет выражен линейной комбинацией контурных интенсивностей для соответствующего источника. Под контурной интенсивностью, понимается поток, циркулирующий в линейно-независимом контуре графа. Контурная интенсивность, создаваемая источником i числено равна потоку в соответствующей хорде [5]. Количество линейно-независимых контуров в графе определяется его цикломатическим числом
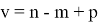

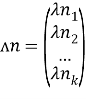
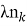

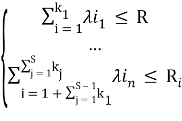
Также необходимо определить целевую функцию с условием минимума. В более общем виде можно разбить все каналы на G групп, и задать, что скорости каналов в рамках этой группы одинаковые, в этом случае целевая функция будет выглядеть следующим образом:
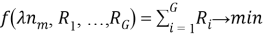
В итоге была получена математическая модель, с помощью которой возможно определить оптимальное распределение трафика при минимальной сумме пропускных способностей в полносвязной сети. Она является базовой так как может быть расширена путем добавления дополнительных ограничений на загрузку каналов, задержки и/или потери информации.
Литература:
- Демичев М. С., Гаипов К. Э. «Алгоритм поиска беспетельных маршрутов» [Электронный ресурс]. URL: https://cyberleninka.ru/article/n/algoritm-poiska-bespetelnyh-marshrutov/viewer
- Гутковская О. Л., Пономарёв Д. Ю. «Применение ортогональной модели телекоммуникационной сети для решения задачи оптимального распределения трафика» [Электронный ресурс]. URL: https://cyberleninka.ru/article/n/primenenie-ortogonalnoy-modeli-telekommunikatsionnoy-seti-dlya-resheniya-zadachi-optimalnogo-raspredeleniya-trafika/viewer
- Гутковская О. Л., Пономарев Д. Ю. «Контурный метод анализа сетей VPN» [Электронный ресурс]. URL: https://elibrary.ru/download/elibrary_25097626_66841561.pdf