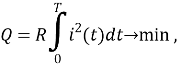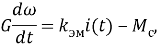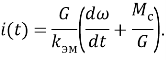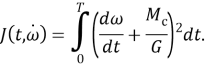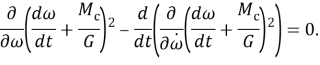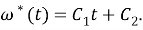В статье рассматривается расчет оптимального тока якоря двигателя постоянного тока, при котором тепловые потери в якоре минимальны, с помощью уравнения Эйлера — Лагранжа. Приведено моделирование уравнения механики электропривода в программном пакете MATLAB с использованием среды моделирования SIMULINK.
Ключевые слова: уравнение Эйлера — Лагранжа, двигатель постоянного тока, минимизация тепловых потерь, MATLAB, SIMULINK.
Одномерное уравнение Эйлера — Лагранжа
Уравнения Эйлера — Лагранжа являются основными формулами вариационного исчисления, c помощью которых ищутся стационарные точки и экстремумы функционалов. Эти уравнения нашли широкое применение в задачах оптимизации, в теоретической физике, в классической механике, римановой геометрии. Эти уравнения используются для нахождения экстремума функционалов [1].
Определим понятие функционала. Пусть дан некоторый класс
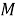
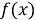
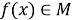
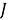
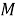
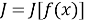
Приведем некоторые примеры функционалов. Рассмотрим множество всех выпрямляемых плоских кривых. С каждой такой кривой связано определенное число –длина. Следовательно, длина кривой – это функционал, определенный на множестве выпрямляемых кривых. Пусть
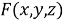
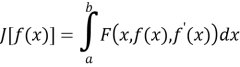
представляет собой функционал, где
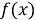
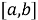
Если функционал
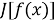
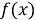
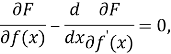
которое называется уравнением Эйлера — Лагранжа.
Также целевая функция
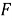
Расчет оптимального значения тока якоря в двигателе постоянного тока
Рассмотрим задачу нахождения функции тока якоря двигателя постоянного тока, при которой тепловые потери в якорной цепи минимальны. Пусть двигатель разгоняется с угловой скорости
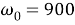
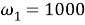
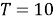
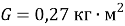
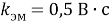
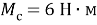
Для решения поставленной задачи необходимо найти такую функцию тока
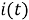
|
|
(1) |
где
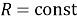
Определим ток в якорной цепи двигателя. Для этого выразим его из уравнения механики электропривода [4]
|
|
(2) |
где
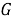
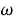
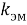
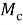
В результате уравнение тока выглядит следующим образом
|
|
(3) |
После этого подставим уравнение тока (3) в выражение (1) и получим тепловые потери в следующем виде
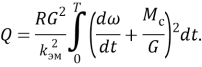
Так как коэффициент перед интегралом есть постоянная величина, то его можно убрать. Тогда функционал
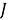
|
|
(4) |
Составим уравнение Эйлера — Лагранжа
|
|
(5) |
Так как
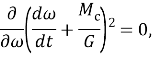
то уравнение (5) примет вид
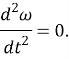
Решение полученного уравнения запишем в виде
|
|
(6) |
С учетом граничных условий определим постоянные
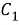
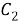
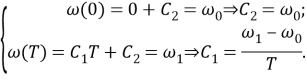
Подставляем найденные
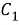
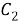
|
|
(7) |
Подставляем функцию угловой скорости (7) в выражение (3) и получаем функцию оптимального тока
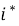
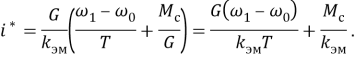
В результате подстановки численных значений величина оптимального тока якоря
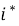
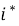
Моделирование в программном пакете MATLAB и SIMULINK
Проверим, действительно ли найденное значение тока
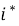
Пусть вариации кривых
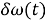
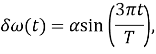
экстремаль имеет вид
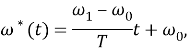
а целевая функция функционала (4) представляет собой выражение вида
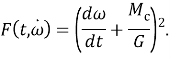
Так как
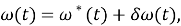
то функция
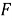
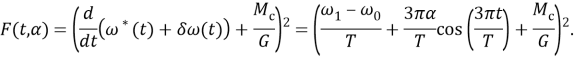
Вычисление функционала (4) реализуем с помощью метода трапеций (листинг 1).
Листинг 1
% функция расчета интеграла
function [I] = Integrate(F, a, b)
n = size(F,2);
I = 0;
for i = 2:1:n-1
I = I + F(i);
end
I = (b - a)/(n - 1)*(F(1)/2 + F(n)/2 + I);
end
% исходные данные
G = 0.27; % момент инерции двигателя, кг*м^2
ke = 0.5; % единый электромагнитный коэффициент, В*с
Mc = 6; % момент сопротивления, Н*м
T = 10; % время разгона, с
w0 = 900; % начальная угловая скорость, рад/с
w1 = 1000; % % конечная угловая скорость, рад/с
n = 100; % количество точек для построения графика
alpha = -30:1:30;
syms t
w_star = t.*(w1 - w0)/T + w0; % экстремаль
delta_w = alpha.*sin(3.*pi.*t./T); % первая вариация
F = (diff(w_star + delta_w, t, 1) + Mc/ke).^2; % целевая функция
% вычисление интеграла
t = linspace(w0,w1,n);
for i=1:1:size(F,2)
if i ~= ceil(size(alpha,2)/2)
J(i) = Integrate(double(subs(F(i))), 0, T);
else
J(i) = Integrate(double(F(i)*ones(1,size(t,2))), 0, T);
end
end
% построение графика
plot(alpha, J);
В результате получили график зависимости функционала
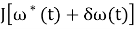
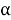
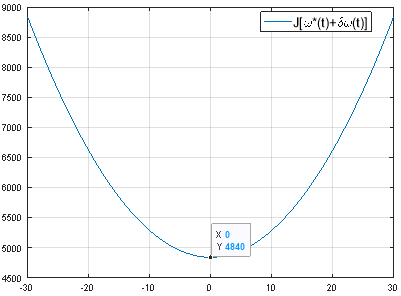
Рис. 1. График зависимости функционала
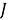
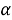
Из рис. 1 видно, что функционал (4) достигает минимума при
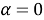
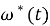
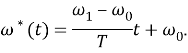
Проведем моделирование системы управления электродвигателем в SIMULINK. Схема моделирования зависимости тока якоря от времени с начальным постоянным током якоря 12 А для соответствующего момента сопротивления 6
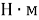
Рис. 2. Схема моделирования уравнения механики электропривода
Напишем код в MATLAB, позволяющий смоделировать схему и построить графики переходных процессов угловой скорости и тока якоря (листинг 2).
Листинг 2
clear;
clc;
G = 0.27; % момент инерции двигателя, кг*м^2
ke = 0.5; % единый электромагнитный коэффициент, В*с
Mc = 6; % момент сопротивления, Н*м
w0 = 900; % начальная угловая скорость, рад/с
i0 = 12; % начальный ток якоря, А
out = sim('bdz1.slx'); % моделирование схемы
figure;
subplot(2,1,1);
plot(out.tout, out.data.signals(1).values); % построение графика w(t)
legend('\omega(t)'); %легенда
set(gca,'FontSize',12); % установка размера шрифта
title('Переходные процессы'); % заголовок
xlabel('Время t, с'); %надпись оси абсцисс
ylabel('Угловая скорость \omega, рад/c'); % надпись оси ординат
ylim([880,1020]); % пределы построения графика по оси ординат
grid on; % включение сетки
subplot(2,1,2);
plot(out.tout, out.data.signals(2).values); % построение графика i(t)
legend('i(t)');
set(gca,'FontSize',12);
xlabel('Время t, с');
ylabel('Ток якоря i, А');
ylim([10,20]);
grid on;
Результат моделирования представлен на рис. 3.
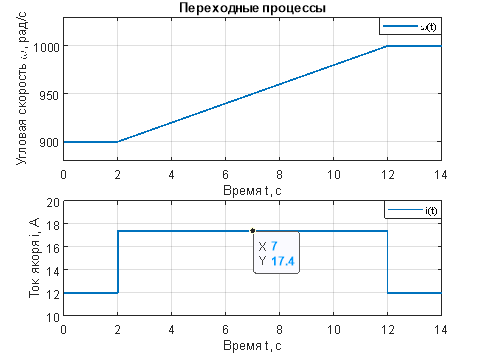
Рис. 3. Зависимости угловой скорости от времени и тока якоря от времени
В результате моделирования системы получили, что при постоянном заданном токе якоря 12 А и постоянном моменте сопротивления 6
Литература:
- Гельфанд И. М., Фомин С. В. Вариационное исчисление. — М.: Государственное издательство физико-математической литературы, 1961.
- Вариационное исчисление, Краснов М. Л., Макаренко Г. И., Киселев А. И. Главная редакция физико-математической литературы изд-ва «Наука», 1973.
- Поникарова И.В. Элементы вариационного исчисления, Учебное пособие. — СПб.: СПбГУ, 2019. — 50 с.
- Усольцев А.А. Электрический привод/Учебное пособие. СПб: НИУ ИТМО, 2012, – 238 с.