В статье показаны способы решения задания № 15 ЕГЭ по информатике.
Ключевые слова: логика, логические операции, законы логики, делимость, Python.
Давно не секрет, что ЕГЭ по информатике достаточно сильно усложнился за последние два года. Теперь от учащихся требуется умение решать задания не только «руками», но с помощью языков программирования. Задача этой статьи помочь разобраться в общем подходе решения заданий № 15 ЕГЭ различными способами.
Рассмотрим пример : ( Демо 2021 ) Обозначим через ДЕЛ( n, m ) утверждение «натуральное число n делится без остатка на натуральное число m ». Для какого наибольшего натурального числа А формула:
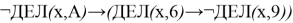
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х )?
Решение:
1) введём обозначения A = ДЕЛ( x , А ) , D 6 = ДЕЛ( x , 6 ) , D 9 = ДЕЛ( x , 9 )
2) введём множества:
A –множество натуральных чисел, для которых выполняется условие A
D 6 –множество натуральных чисел, для которых выполняется условие D 6
D 9 –множество натуральных чисел, для которых выполняется условие D 9
3)
Запишем формулу в новых обозначениях
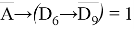
4) Раскроем импликацию по правилу:
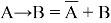
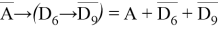
Дизъюнкция истинна, когда хотя бы одно из выражений истинно. Поэтому, чтобы однозначно определить A , рассмотрим «опасный» случай. Назовем «опасными» такие значения х , которые обращают в ложь выражение:
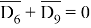
Числа, которые делятся на 6, обращают в ложь утверждение
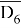
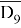
Чтобы дизъюнкция
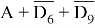
Ответ: 18
Для лучшего понимания изобразим множества чисел с помощью кругов Эйлера (рисунок 1). D 6 — множество чисел на которые делится число 6. D 9 — множество чисел на которые делится число 9.
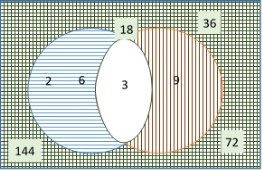
Рис. 1
На рисунке красная вертикальная штриховка обозначает множество чисел
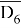
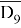
Для истинности всего выражения множество A должно перекрыть белую область. Это обязательный минимум. Для максимального значения, необходимо перекрыть области с одинарной штриховкой. На рисунке это область объединения кругов. Максимальное A=18 . Брать большие значения не имеет смысла, так как при них выражение будет истинно независимо от A .
Первые два метода решения данного задания требуют вдумчивого разбора и глубокого понимания темы. ЕГЭ, проводимый в компьютерной форме, позволяет быстро решить данную задачу с помощью программирования. Ниже представлена программа на языке Python:

Во внешнем цикле в обратном порядке перебираем произвольные значения A , начиная с заведомо большего (выбираем его произвольно и лучше запустить программу с разными значениями). Во внутреннем цикле перебираем значения х , начиная с минимального, равного двум. Конечное значение также выбираем произвольно. В условие записываем преобразованное выражение (см. п. 4). Если переменная flag не поменяет своего значения, то первое найденное значение A , будет выведено на экран.
Пример 2 . Обозначим через ДЕЛ ( n , m ) утверждение «натуральное число n делится без остатка на натуральное число m ». Для какого наибольшего натурального числа А формула
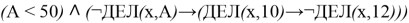
тождественно истинна, т. е. принимает значение 1 при любом натуральном х ?
Решение:
По аналогии с первым заданием введём обозначения: A = ДЕЛ ( x , А ) , D 10 = ДЕЛ ( x , 10 ) , D 10 = ДЕЛ ( x , 12 ) изапишем формулу в упрощенном виде:
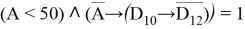
Преобразуем правую часть выражения по правилу:
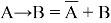
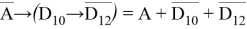
«Опасными» будут такие значения х , которые обращают в ложь выражение:
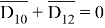
т.е числа, которые одновременно делятся и на 10 и на 12. НОК = 30 и дальше числа: 60, 90, 120 и т. д.
Чтобы дизъюнкция
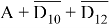
Ответ: 30
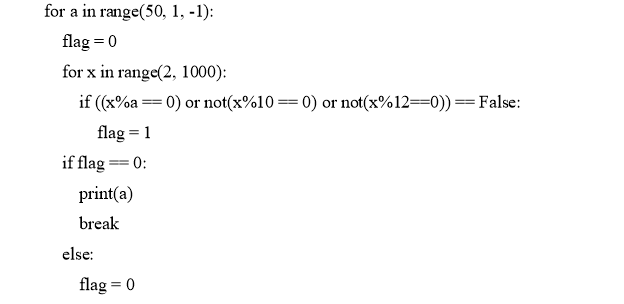
Пример 3 . (СтатГрад 10.12.2020) Обозначим через ДЕЛ ( n , m ) утверждение «натуральное число n делится без остатка на натуральное число m ». Для какого наибольшего натурального числа А формула
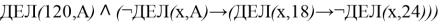
тождественно истинна, то есть принимает значение 1 при любом натуральном х ?
После преобразований правая часть выражения примет вид:
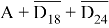
НОК = 72.
Все возможные делители числа 72: 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72. Учитывая левую часть выражения
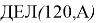
Ответ: 24
Решение на Python:
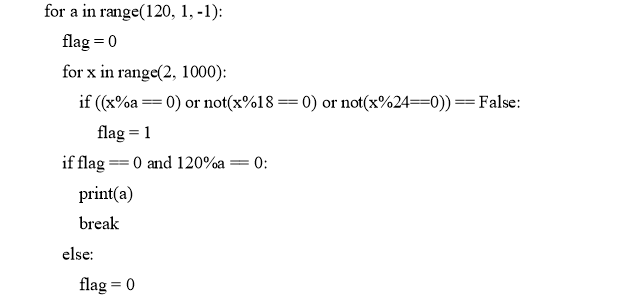
Пример 4 . Обозначим через ДЕЛ( n , m ) утверждение «натуральное число n делится без остатка на натуральное число m ». Для какого наименьшего натурального числа А формула
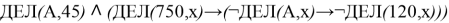
тождественно истинна, то есть принимает значение 1 при любом натуральном х ?
В отличие от предыдущих заданий, в этом примере число делится на х . Необходимо учесть, что числа должны одновременно разделиться на х , поэтому в заданиях такого типа необходимо найти НОД.
После преобразований правая часть выражения примет вид:
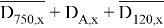
НОД = 30.
Для наглядности изобразим множества делителей с помощью кругов Эйлера.
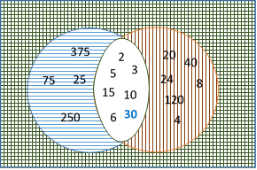
Рис. 2
На рисунке 2 красная вертикальная штриховка обозначает множество чисел
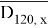
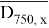
Для истинности всего выражения множество A должно перекрыть белую область. Из всех возможных чисел, выбираем максимальное 30, так как если А делится на 30, то оно разделится и на остальные числа.
Но в задании есть еще левая часть:
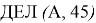
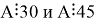
Минимальное А = 90
Ответ: 90
Решение на Python:
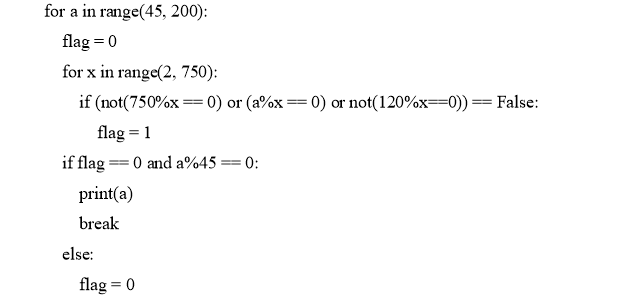
Пример 5 . (Демо 2023) Обозначим через ДЕЛ( n , m ) утверждение «натуральное число n делится без остатка на натуральное число m ». Для какого наименьшего натурального числа А формула
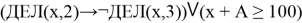
тождественно истинна (т. е. принимает значение 1) при любом натуральном значении переменной х ?
Преобразуем левую часть выражения:
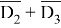
Для того чтобы все выражение было истинным, достаточно чтобы была истинна любая часть выражения. Поэтому, чтобы однозначно определить A , рассмотрим «опасный» случай. Назовем «опасными» такие значения х , которые обращают в ложь выражение:
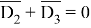
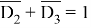
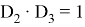
Таким образом, в ложь дизъюнкцию обращают числа, которые одновременно делятся и на 2 и на 3. Для нашего примера НОК = 6 .
Подставляем найденное значение х в правую часть выражения:
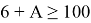
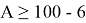
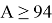
Ответ: 94
Решение на Python:
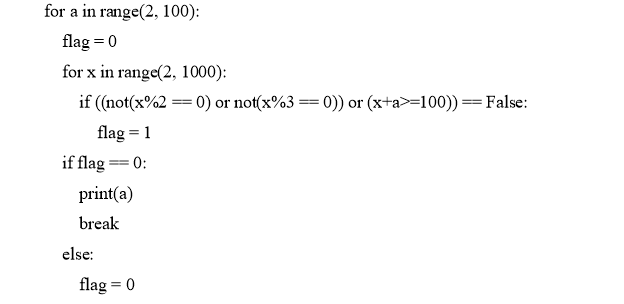
Пример 6 . Обозначим через ДЕЛ ( n , m ) утверждение: «Натуральное число n делится без остатка на натуральное число m ». Для какого наименьшего натурального числа А формула:
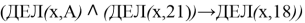
тождественно истинна (т. е. принимает значение 1 при любом натуральном значении переменной х )?
Введем обозначения и преобразуем данное выражение:
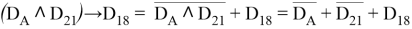
Чтобы однозначно определить А, необходимо чтобы
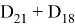
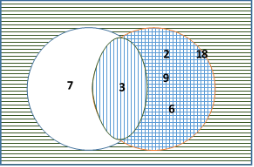
Рис. 3
Ответ: 18
Решение на Python:
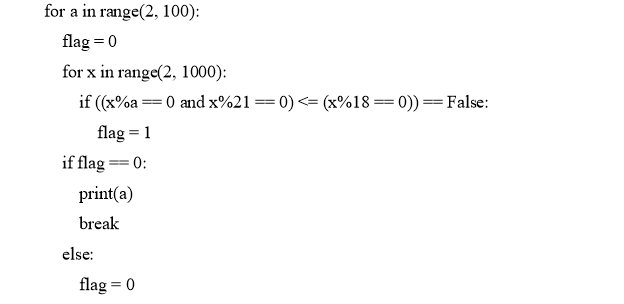
Литература:
- Мирончик Е. А., «Алгебра предикатов и построение геометрических моделей на ЕГЭ по информатике» — URL: https://kpolyakov.spb.ru/download/mea-2019–03.pdf (дата обращения: 25.11.2022). — Текст: электронный.
- Поляков К. Ю., «Множества и логика в задачах ЕГЭ» — URL: https://kpolyakov.spb.ru/download/inf-2015–10.pdf (дата обращения: 25.11.2022). — Текст: электронный.
- ФГБНУ «Федеральный институт педагогических измерений»: официальный сайт. Москва. — URL: https://fipi.ru/ (дата обращения: 21.11.2022). — Текст: электронный.







