В древности наши предки строили круглые белые дома. Потому что они знали, что, делая это, можно покрыть больше площадей с меньшим количеством материала. Движения Земли, Луны, планет и спутников также осуществляются по орбитальным путям. Дороги в виде круга, окружающие территории очень важны в жизни. Для всего этого есть несколько причин, например, тот факт, что круглые дороги в целом более удобны и требуют меньшего количества материала для создания.
Круги также широко используются в декоративных работах. Круги — одна из наиболее часто используемых геометрических фигур в человеческой деятельности. Древнегреческий философ (570–500 гг. до н. э.) Пифагор Самосский также говорил: «Самая прекрасная из всех фигур — это круг». Имея это в виду, в данной статье рассматривается вопрос о важности развития городов с помощью кольцевых дорог.
Городские дороги удобнее, когда они построены концентрическими окружностями (кольцами), чем другие типы. Во-первых, если дороги будут построены по кругу, длина дорог сократится. Стоит рассмотреть несколько примеров, чтобы убедиться в этом.
Периметр любого правильного многоугольника, вписанного в окружность, является приблизительной длиной окружности. Чем больше число сторон такого многоугольника, тем выше точность этого приближения.
Потому что с увеличением количества сторон, правильный многоугольник меньше отличается от круга (рис. 1).

Рис. 1
Когда число сторон правильного многоугольника, вписанного в окружность, умножается на бесконечность, предел стремления его периметра является точным значением длины окружности.
Теперь сравним периметры правильных многоугольников равной площади. Для этого определим периметр правильных многоугольников через их площадь.
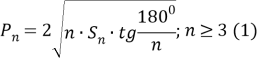
(Здесь n — число сторон правильного многоугольника, S n — площадь правильного многоугольника, a n — его сторона, P n — периметр, r и R — соответственно радиусы вписанных окружностей внутри и снаружи).
Действительно, мы можем использовать формулы
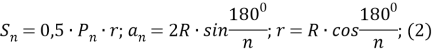
для вычисления площади, стороны и радиуса круга, вписанного в правильный многоугольник.

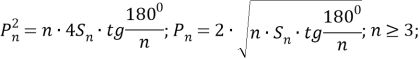
Теперь примем площади правильных многоугольников за 100 квадратных метров (S n = 100 кв.м.). В этом случае наша формула (1) будет выглядеть так.
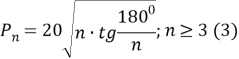
Тогда, если посчитать по формуле
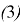
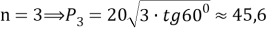
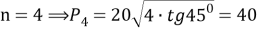

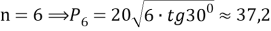
Таким образом:
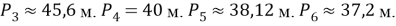

Рис. 2
Теперь построим круг площадью в 100 квадратных метров и рассчитаем ее длину (рис. 2).

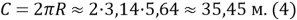
Как видно из этого, длина окружности будет меньше периметра любого правильного многоугольника при равенстве площадей, то есть длина пути будет меньше, если пути будут круговыми.
Итак, если сравнить круговые пути вокруг квадратной формы, то строительство будет менее затратным и получится путь

Литература:
- Беклемишев, Д. В. Курс аналитической геометрии и линейной алгебры: учебник для вузов / Д. В. Беклемишев. — 19-е изд., стер. — Санкт-Петербург: Лань, 2022. — 448 с. https://e.lanbook.com/book/189312
- Клетеник, Д. В. Сборник задач по аналитической геометрии: учебное пособие для вузов / Д. В. Клетеник; Под редакцией Н. В. Ефимова. — 17-е изд.,стер. — Санкт-Петербург: Лань, 2022. — 224 с. https://e.lanbook.com/book/187823
- Проскуряков, И. В. Сборник задач по линейной алгебре: учебное пособие для вузов / И. В. Проскуряков. — 16-е изд., стер. — Санкт-Петербург: Лань, 2022— 476 с. https://e.lanbook.com/book/183752







