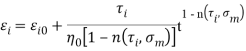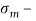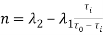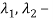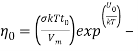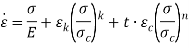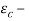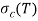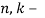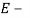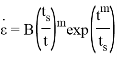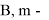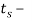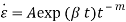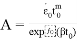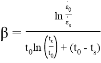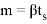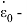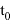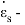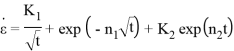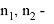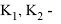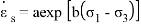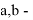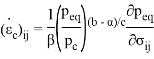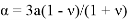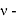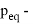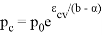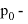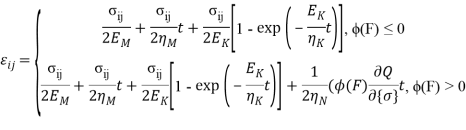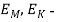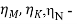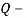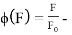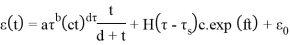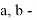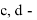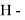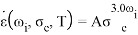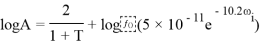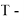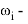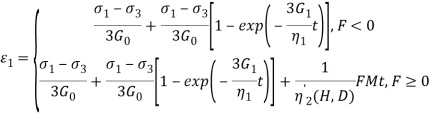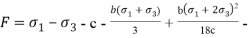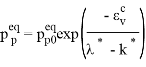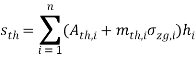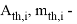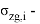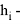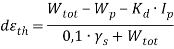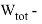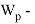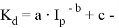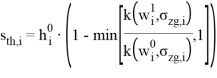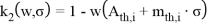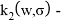Реологические модели мерзлых грунтов



В статье проанализированы существующие исследования в области математических реологических моделей мерзлых грунтов. Рассмотрены имеющиеся варианты моделирования реологических процессов в мерзлых грунтах, теории деформирования и соответствующие им уравнения деформирования. Проанализированы параметры численных моделей, описывающих поведение немерзлых грунтов (Soft Soil Creep Model), также модифицированную модель оттаивающего грунта по СП 25.13330, реализованную в ПК Frost 3D. Рассмотрены имеющиеся термомеханические модели в действующих нормативных документах. Выявлены неточности моделирования процесса деформирования мерзлых грунтов и необходимость дальнейшего исследования высокотемпературных грунтов и усовершенствования как моделей, так и существующей нормативной базы.

Ключевые слова: мерзлые грунты, теории деформирования, реологические свойства, модели поведения мерзлого грунта

1 Введение

Нелинейные модели поведения немерзлых грунтов разрабатывались примерно с 1950-х гг/ различными исследователями [1, 2, 3, 4, 5 и др.].], и на сегодняшний день используются в практике численного моделирования довольно успешно в различных проектах. Однако, неоднократно отмечалось [6, 7, 8, 9, 10 и др. что эти модели требуют несколько иного подхода к инженерным изысканиям, по сравнению с традиционными методами проектирования и расчета оснований. Нелинейные модели для мерзлых грунтов также разрабатывались, однако широкого распространения не получили. На сегодняшний день в России чаще всего применяется аналитическая модель оттаивающего грунта [11, 22], в которой рассматривается только случай полностью оттаявшего грунта. Расчет температурного поля грунтов представляет собой отдельную теплофизическую задачу, решение которой базируется на уравнениях Фурье и Стефана [12 и др.]. В связи с этим, авторами произведена попытка анализа существующих механических и реологических моделей мерзлых грунтов и оценка их применимости в задачах, связанных с расчетом НДС пластичномерзлых грунтов.

2 Реологические модели грунта

Для твердомерзлых и пластичномерзлых грунтов при деформировании характерно проявление ползучести: развитие деформаций грунта с течением времени под действием постоянной нагрузки. Это обусловлено наличием льда и незамерзшей воды [11, 13 и др.]. На кривой выделяют три характерных участка (стадий): I–первичная затухающая ползучесть с затухающей скоростью деформации; II– вторичная ползучесть с почти постоянной скоростью деформации; III–третичная ползучесть с увеличивающейся скоростью деформации.

Стадии ползучести в основном определяются совокупностью эффектов разрушения начальной структуры, появления и последующего развития трещин и упрочнения мерзлого грунта.

Базисная (характерная) кривая ползучести представлена на рис.1.

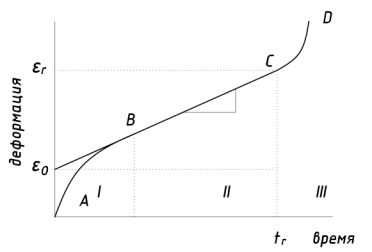
Рис. 1. Базисная кривая ползучести: I, II, III — стадии ползучести

В значительной степени ползучесть зависит от колебания температуры, скорости деформации, а также величины внешней нагрузки. Из-за чувствительности мерзлых грунтов к температуре и уровню напряжения их механические свойства более сложны, в сравнении с немерзлыми грунтами.

В настоящее время для описания ползучести мерзлых грунтов применяются механические модели, а также микроскопическая и феноменологическая теории деформирования. Для микроскопических моделей свойственно введение параметров термодинамики и механики повреждений [14, 15, 16 и др.], однако получение значений данных параметров в лабораторных условиях затруднено. Большее применение имеют феноменологические модели. Для расчета деформаций на стадиях ползучести были получены эмпирические и полуэмпирические модели [17, 18, 19, 20 и др.], тем не менее они не пригодны для задач со сложными условиями, так как выведены для определенных условий опыта.

При описании ползучести мерзлых грунтов в механических моделях используют различные комбинации упругого, вязкого и пластичного элементов (рис. 2).

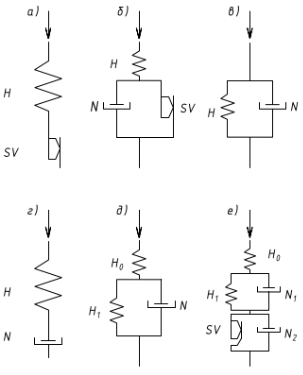
Рис. 2. Механические реологические модели: а) Прандтля; б) Бингама; в) Кельвина– Фойгта; г) Максвелла; д) Хохэнемзера–Прагера; е) Вялова

Так как реальные свойства мерзлых грунтов описать трудно, то теорию механических моделей необходимо применять только с использованием опытных данных.

3 Анализ математических моделей деформирования мерзлых грунтов

Большое количество численных моделей немерзлых грунтов, описывающих поведение грунта при деформировании, не зависят от фактора времени. Для слабых грунтов фактор времени является значимым, так как при продолжительном нагружении грунт продолжает деформироваться в следствие ползучести.

Согласно действующим нормативным документам, расчет осадки основания производится только для грунта в полностью оттаявшем состоянии, без учета незавершенных фазовых переходов. Так же необходимо отметить, расчет производится только для конечного момента времени.

Из рассмотренных моделей грунта можно сделать вывод, что не существует единой модели для описания учета изменения как температуры, так и свойств мерзлых и талых грунтов. Большое число уравнений основываются на подобных зависимостях для металлов. Также описание изменяемости структуры в процессе деформирования происходит за счет процессов, приводящих к упрочнению или расслаблению грунта на основе макроскопических опытов, то есть вносится элемент эмпирики. Нахождение значений в основном осуществляется путями итерации и интерполяции значений, полученных из серии испытаний в соответствующем диапазоне. Расчетные реологические параметры согласуются с данными испытаний, в то время как параметры прочности и свойств изменяются или не учитываются. Совместное влияние факторов предусматривается лишь в некоторых моделях, что увеличивает их достоверность и практическую значимость.

В таблице 1 приведено математическое выражение имеющихся моделей и зависимостей процесса деформирования отечественного и зарубежного опыта.

Таблица 1

Автор	Выражение	Параметры	Учет изменения температуры	Учет изменения свойств
1. Вялов С. С		отражает влияние среднего нормального напряжения; , структурные параметры; исходная вязкость	Да	Нет
3. Ladanayi		произвольная скорость деформирования при заданном напряжении и температуре ; постоянные грунта; модуль упругости	Да	Нет
4. A. Assur		параметры, зависящие от напряжений и температуры; время до начала минимума скорости ползучести	Да	Н/д
5. A. Fish, J.Ting		; ; ; скорость деформации на начальное ненулевое время ; минмум скорости деформации ползучести	Н/д	Н/д
6. R.Goughnour, O.Andersland		параметры грунта в зависимости от температуры; коэффициенты, зависящие от напряжения и температуры соответственно	Да	Н/д
7. Jia et al., Zhao. X et al.		где параметры, связанные со временем и давлением консолидации	Нет	Нет
9. X. Yao, J. Qi, M. Liu, F.Yu		; коэффициент Пуассона; эквивалентное напряжение, принимаемое как функция пластического потенциала; , начальное изотропное напряжение предварительного уплотнения	Н/д	Да
10. S. Wang, J. Qi, Z. Yin, J. Zhang, W. Ma		модули упругости тел Максвелла и Кельвина соответственно; коэффициенты вязкости для тел Максвелла, Кельвина и Бингама соответственно; вязкопластическая потенциальная функция; масштабирующая функция	Да	Да
11. M. Liao, Y. Lai, J. Yang, S. Li		температурный параметр и параметр реологической чувствительности напряжения; параметры реологии; параметр упрочнения	Да	Н/д
12. Glen		абсолютное значение температуры в градусах Цельсия ниже 0ºС; объемная льдистость функция температуры и объемной льдистости; инвариант напряжения	Да	Да
13. Xin Li, Enlong Liu, Bingtang Song, Xingyan Liu		; функция текучести; модуль сдвига упругого тела; модуль сдвига вязкоупругого тела; коэффициент вязкости; коэффициент эффективной вязкости в вязкопластичном теле	Да	Да
14. Soft Soil Creep Model		матрица упругости; функция пластического потенциала;	Нет	Да
15. СП 25.13330.2020		коэффициент оттаивания и коэффициент сжимаемости; вертикальное напряжение от собственного веса грунта в середине i -того слоя; толщина i -того оттаивающего слоя	Н/д	Н/д
16. Киселев М. Ф		суммарная влажность грунта; влажность на границе раскатывания; коэффициент уплотняемости	Нет	Да
17. Frost 3D (модифицированная методика СП 25.13330.2020)		функция безразмерной высоты грунта, зависящий от доли незамерзшей воды и нагрузки на образец грунта	Н/д	Да

4 Вывод

Результаты изучения отечественных и зарубежных исследований показывают, что число реологических моделей с точным описанием всего процесса деформирования мерзлых и талых ограничено. Кроме того, существует меньше доступных моделей ползучести, учитывающих влияние температуры, напряжения и времени в совокупности, что снижает достоверность и практическую значимость моделей.

Большинство моделей описывает поведения мерзлых грунтов или талых, в то время как наиболее актуальным вопросом сейчас является явление рассмотрение деформирования пластично-мерзлых грунтов. Поэтому необходимы дальнейшие исследования моделей поведения пластичномерзлых грунтов и усовершенствование нормативной базы в данном направлении.

Литература:

1. Drucker, D. C., Prager, W. Soil mechanics and plastic analysis for limit design. Quarterly of Applied Mathematics, vol. 10, no. 2, 1952.
2. Цытович Н. А. Механика грунтов. Учебное пособие. Изд. 4-е перераб. доп. М.: Стройиздат, 1963.
3. Roscoe, K.H., Burland, J. B. On the generalized stress-strain behaviour of ‘wet’ clay, in: J. Heyman, F. Leckie (Eds.), Engineering plasticity, Cambridge University Press, Cambridge, 535–609, 1968.
4. Drucker, D. C., Prager, W. Soil mechanics and plastic analysis for limit design. Quarterly of Applied Mathematics, vol. 10, no. 2, 1952.
5. Vermeer P. A., De Borst R. Non-associated plasticity for soils, concrete and rock. Heron. Vol. 29. № 3, 1984.
6. Бате К., Вилсон Е. Численные методa анализа и метод конечных элементов. Под ред. А. Ф. Смирнова.–М.: Стройиздат, 1982.
7. Шашкин А. Г., Шашкин К. Г. Упруго-вязкопластическая модель структурно-неустойчивого грунта. Развитие городов и геотехническое строительство. № 9. СПб.: Изд-во «Геореконструкция–Фундаментпроект», 2005.
8. Мирный А. Ю., Тер-Мартиросян А. З. Области применения современных математических моделей. Геотехника. № 1, 2017.
9. Бершов А. В. Особенности проведения инженерно-геологических изысканий для обеспечения конечно-элементных геотехнических расчетов в нелинейной постановке. Всеросс. Форум высотного и уникального строительства 100+, 2019.
10. Бершов А. В., Мирный А. Ю., Усов А. Н. Определение модуля деформации разгрузки в дисперсных грунтах и методы его учета при проектировании. ОФМГ, № 1, 2020.
11. Цытович Н. А. Механика мерзлых грунтов. Учебн. пособие. М., «Высш. школа», 1973.
12. Ершов Э. Д. Общая геокриология. Учебник–М., Из-во МГУ, 2002.
13. Вялов С. С. Реологические процессы в мерзлых грунтах и условие их предельного равновесия. Изд-во АН СССР, 1957.
14. Fish, A. M. Comparison of USSR codes and US Army manual for design of foundation on permafrost. Cold Reg. Sci. and Techn., Vol.8, No. 1, 1983.
15. Miao T, Wei X, Zhang C. Micro-stuctural damage theories of creep of frozen soil. Science in China (Series B) 25(03), 1995.
16. He P, Cheng G, Zhu Y. Viscoelastic plastic damage constative theory of frozen soil. Science in China: Series D 29(S1), 1999.
17. Goughnour R. R., Andersland O. B. Mechanical properties of a sand-ice system. Journal of the Soil Mechanics and Foundation Division, ASCE, 94 (SM 4), 1968.
18. Ting, J.M, R.T Martin. Application of the Andrade Equation to Creep Data for Ice and Frozen soil. Cold Reg. Sci. and Techn., 1(1), 1979.
19. Assur, A. Some promising trends in ice mechanics. Physics and Mechanics of Ice. Springer, Berlin, 1980.
20. Zhu, Y.L., Carbee D. L. Creep behavior of frozen silt under constant uniaxial stress. In: Priceedinggs of the 4th International Conf. on Permafrost, Fairbanks, Alaska, 1983.
21. Сахаров И. И, Кудрявцев С.А, Парамонов В. Н. Промерзающие, мерзлые и оттаивающие грунты как основания зданий и сооружений/Под ред. Сахарова И.И, Москва, Изд-во Ассоциации строительных вузов, 2021.
22. СП25.13330.2020. Основания и фундаменты на вечномерзлых грунтах.