В настоящей статье на основе разработанной методики и алгоритма расчета на прочность и устойчивость внезапно повреждаемых рамных систем, рассмотрено развитие этого решения с учетом особенностей разрушения железобетонных элементов. Рассматриваются нагружения рамной системы и изменения конструктивных и расчетных схем, которые вызваны образованием пластических шарниров, в таких системах возникают односторонние моментные связи. В основу расчета рамы положена идея построения расчетной схемы по аналогии с расчетными схемами многосвязных пространственных систем коробчатого типа, обеспечивающие неизменяемость структуры исходных уровней при видоизменении расчетной схемы.
Ключевые слова: конструктивная безопасность , устойчивость, проблема, запроектные воздействия, метод расчета, пластический шарнир, конструктивно-нелинейное система,статико-динамическая нагружения, вантовая система, локальное разрушение.
Введение
В настоящее время с развитием индустриализации, здания и сооружения с многофункциональным и высоким уровнем архитектурной сложности зданий, а также с постоянным увеличением воздействий техногенного и природного характера, решение задач их безопасности все более усложняется. На сегодняшний день метод предельных состояний, используемый для оценки надежности строительных конструкций, является основой для расчета безопасности конструкций и конструктивных систем. Однако, конструкции, построенные в соответствии с требованиями традиционного метода предельных состояний, не всегда бывают достаточно устойчивыми под действием неожиданных « запроектных » воздействий.
В основу критериев для рассматриваемого особого предельного состояния железобетонных элементов статически неопределимых конструктивных систем зданий и сооружений исследованы научных публикациях [1,2]. По результатами исследования было принято условие ограничения предельных прогибов конструкции после удаления одного из элементов. Превышение этого прогиба конструкции принимается как исчерпание несущей способности. В то же время расчет прогибов железобетонных элементов рассматриваемых рамных систем с использованием традиционных диаграмм состояния «момент-кривизна», тем более статических, может быть выполнен до уровня нагрузки, когда железобетонный элемент разрушается по сжатому бетону, разделяется на отдельные блоки и превращается в висячую систему [3]. Но такие методы решения ограничиваются первыми двумя критериями разрушения, которые определяются ограничением предельных деформаций материалов конструкции. Работ, посвященных исследованию деформирования железобетонных конструктивных систем при их трансформировании из жёстких в висячие системы крайне мало, а имеющиеся решения, даже такие обстоятельные как [4,5] также используют диаграммы статического деформирования бетона и арматуры.
В связи с этим, в рассматриваемой статье приведен алгоритм и методика определения параметров статико-динамических диаграмм деформирования железобетонных элементов статически неопределимых конструктивных систем при их внезапной структурной перестройке от особого воздействия, вызванного внезапным удалением из конструктивной системы одной из несущих конструкций.
Методы расчета
Рассмотрим диаграмму состояний сечения железобетонного элемента «параметрическая нагрузка-прогиб ( m f )». Конструктивно-нелинейное система при статическом и статико-динамическом нагружении на всех уровнях ее деформирования в общем виде можно представить графиками рисунка 1.
По мере нагружения рамно-стержневой системы до уровня crc Pi (рис. 1) в напряженном сечении одного из элементов конструктивной системы начинается образование трещин. В последствии происходит изменение жесткости сечении элемента с начальной жесткости B0=tgα0 на жесткость элемента с трещинами Bcrc=tgαcrc . Расчеты этой жесткости элемента вычисляются по известным в теории железобетона зависимостям, например по формулам работы [6].
При дальнейшем нагружении рамной конструкции статистической нагрузкой продолжается процесс трещинообразования элементов рамы, после некотором уровне нагрузки λ1 Pi в одном из сечений наиболее напряженного элемента образуется первый пластический шарнир. Дальнейшее увеличение нагрузки на раму приведет к образованию в ригеле второго λ2 Pi и затем третьего λ3 Pi пластических шарниров после которого рассматриваемый элемент превращается из жесткого в гибкий. Арматурные стержни ригели начинают работать на растяжение как вант.
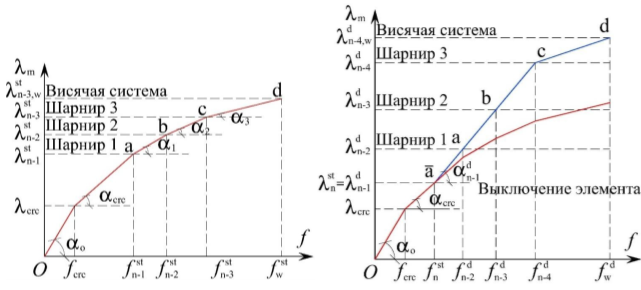
а б
Рис. 1. Диаграммы состояний сечения железобетонного элемента «параметрическая нагрузка-прогиб ( λm – f )» физически и конструктивно нелинейной системы: а — при статическом нагружении; б — при статическом нагружении и динамический догруженный
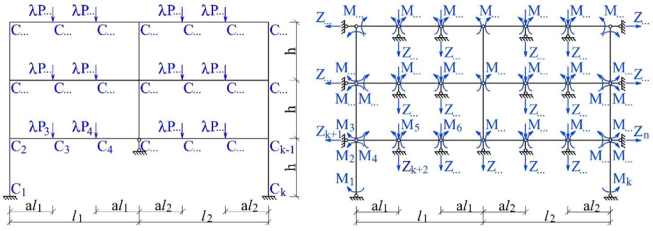
а б
Рис. 2. Заданная (а) и основанная (б) система смешанного метода для определения параметрической нагрузки
После приложения к нагруженной конструктивной системе особого воздействия в виде внезапного удаления стойки из рамной системы происходит уменьшение ее статической неопределимости и перераспределение силовых потоков от структурной перестройки конструктивной системы. Соответственно изменяются усилия M j в сечениях ригелей рамы и изменяется режим нагружения сечения ригеля со статического на динамический. Для определений усилий M j после воздействия может быть выполнено с использованием неординарного варианта смешанного метода, разработанного И. Е. Милейковским, В. И. Колчуновым [7]. Суть метода состоит в том, что основная система смешанного метода расчета выбирается в виде шарнирно-стержневого полигона с удаленными в местах возможного выключения связями и заменой их неизвестными Mj ( j =1,2,..., k ) (рис. 2.). Если при удалении связей образуется геометрически изменяемая основная система, то накладываются дополнительные связи Zi ( i = k +1, k +2,..., n ). Выбор смешанного метода для решения поставленной задачи хотя и приводит к увеличению числа неизвестных исходной системы уравнений, но при этом значительно сокращается трудоемкость расчетов, связанных с выявлением последовательности выключения связей и анализом геометрической неизменяемости системы. При применении смешанного метода нами виде выключение связей не приводит к изменению основной системы уравнений с учетом того, что независимо от местоположения сечения, где произошло выключение связи, число неизвестных всегда уменьшается на единицу.
При этом этап статического нагружения при начальной жесткости элемента до уровня λcrcPi остается неизменным. Затем, при дальнейшем нагружении n-раз статической неопределимой конструктивной системы до уровня заданной статической нагрузки λstn (рис. 1б) сечение ригеля деформируется, как и в случае статического нагружения исходной n-раз статически неопределимой рамы.
С использованием выбранной описанным образом основой системы может быть определена относительная параметрическая нагрузка mPi при которой в наиболее напряженном сечении ригеля достигаются один из критериев особого предельного состояния при статико-динамическом нагружении рамы. Как и при статическом нагружении, индекс m определяет уровень относительной нагрузки λmPi при которой после приложения особого воздействия в виде удаления одной из стоек рамы в одном из сечений наиболее нагруженного ригеля примыкающего к удаляемой стойке достигается предельный момент, т. е. образуется первый пластический шарнир. Затем по мере роста динамической нагрузки образуется второй и третий шарниры. Если после образования третьего пластического шарнира деформации арматуры не достигают предельных значений и не нарушается ее анкеровка в опорных сечениях ригеля, то конструкция неразрезного ригеля из жесткой превращается в изменяемую вантовую систему, сопротивляющуюся только растяжению. На диаграмме ( λm – f )» эта относительная нагрузка обозначена λdт-4,w . В этом случае производится проверка третьего критерия особого предельного состояния — критерия предельно допустимого прогиба конструкции fwd .
Критериальная проверка устойчивости физический и конструктивно нелинейной системы при особом воздействии производится на основе расчета параметров диаграммы «( λm – f )». Выключение моментной связи (образование пластического шарнира с ограниченной ветвью деформирования) в одном из элементов рамной системы после удаления одной из стоек рамы произойдет в случае, когда при предельном моменте
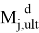
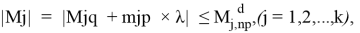
где
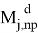
В левой части системы неравенств (1) значение
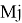
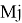
Минимальное значение параметрической нагрузки λ m(m=1,2,3) при которой в наиболее нагруженном сечении ригеля С j при рассматриваемом особом воздействии достигается предельное значение момента может быть определено по формуле:
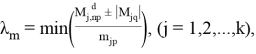
Знак «минус» в числителе принимается если M jq и m jp совпадают и наоборот.
Критерием прогрессирующего обрушения рамы будет образование геометрически изменяемой вантовой системы после выключения очередной связи. Для выявления этого критерия на каждом шаге после выполнения преобразований системы уравнений вычисляется определитель матрицы коэффициентов при неизвестных. Если определитель равен нулю, то имеем геометрически изменяемую вантовую систему. В противном случае живучесть системы не исчерпана и решение следует продолжать.
Окончание стадии деформирование ригелей рамы как неизменяемой конструкции λ = λ m(m=n-2, n-3, n-4) происходит тогда, когда в трёх сечениях ригеля достигаются предельные значения моментов и происходит локальное разрушение сечений по сжатому бетону при ε b = ε bu (рис. 3.).
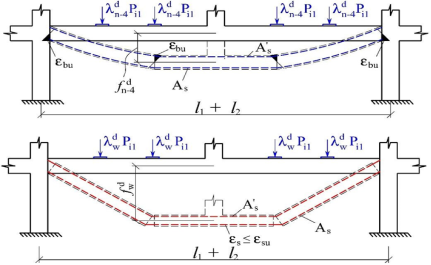
Рис. 3. Схемы перемещений в рассматриваемой подконструкции ригеля как упруго-жестко-пластического тела (a) и как ванта (б)
До этого момента перемещения (прогибы) сечений, где достигаются предельные деформации бетона ε b = ε bu происходят как в жестко-пластическом теле от изгиба и поворота сечений. Если деформации арматуры не достигают предельных значений ε s = ε su то работа конструкции ригеля переходит из стадии упруго-жестко-пластического деформирования в стадию работы как висячей системы, когда в качестве растянутых вант выступает арматура A s и A s ’ (рис. 3б)
Жесткие бетонные блоки «зависают» на арматурных стержнях (вантах) и предельное значение прогиба ригеля на этом этапе определяется как для вантовой системы по известным зависимостям строительной механики. Критерием особого предельного состояния в этом случае становится максимальный прогиб f = f w d определяемый расчетом как для висячей системы. Опытные данные об относительном значении этого прогиба до разрыва арматуры в испытаниях разных авторов существенно разнятся и составляют от 1/30 пролета в исследованиях [8] до 1/20 и даже 1/10 в исследованиях [4]. Все измеряемые величины были получены с применением элементов упругих оболочек [9,10].
Заключение
Рассматривалась методика определения параметров диаграммы состояний сечений «относительная нагрузка-прогиб» и деформационный критерий особого предельного состояния железобетонного элемента статически неопределимых рамно-стержневых конструктивных систем железобетонных элементов при особом воздействии, вызванном удалением из конструктивной системы одного из несущих элементов. Рассмотрены два этапа нагружения таких систем: нагружение статической нагрузкой до заданного проектного уровня и догружение динамической нагрузкой, вызванной внезапной структурой.
Литература:
- Алмазов В. О. Проблемы прогрессирующего разрушения / Алмазов В. О. // Строительство и реконструкция — 2014. — Т. 6 — № 56 — С.3–10.
- Травуш В. И. Проектирование защиты крупнопанельных зданий от прогрессирующего обрушения / Травуш В. И., Шапиро Г. И., Колчунов В. И., Леонтьев Е. В., Федорова Н. В. // Жилищное строительство — 2019. — № 3 — С.40–46.
- Choi H. Progressive collapse-resisting capacity of RC beam–column sub- assemblage / Choi H., Kim J. // Magazine of Concrete Research — 2011. — Т. 63 — № 4 — С.297–310.
- Alogla K. Theoretical assessment of progressive collapse capacity of reinforced concrete structures / Alogla K., Weekes L., Augusthus-Nelson L. // Magazine of Concrete Research — 2017. — Т. 69 — № 3 — С.145–162.
- Mohajeri Nav F. Analytical investigation of reinforced concrete frames under middle column removal scenario / Mohajeri Nav F., Usefi N., Abbasnia R. // Advances in Structural Engineering — 2018. — Т. 21 — № 9 — С.1388–1401.
- Kolcunov V. I. Deformation and failure of a monolithic reinforced concrete frame under accidental actions / Kolcunov V. I., Tuyen V. N., Korenkov P. A. // IOP Conference Series: Materials Science and Engineering — 2020. — Т. 753 — С.032037.
- Травуш В. И. Расчет параметра живучести рамно-стержневых конструктивных систем / Травуш В. И., Федорова Н. В. // Научный журнал строительства и архитектуры — 2017. — № 1 — С.21–28.
- Alshaikh I. M. H. Progressive collapse of reinforced rubberised concrete: Experimental study / Alshaikh I. M. H., Abu Bakar B. H., Alwesabi E. A. H., Akil H. M. // Construction and Building Materials — 2019. — Т. 226 — С.307–316.
- I. Polyakova, R. Imambayeva, B. Aubakirova. Determination of dynamic characteristics of elastic shell structures. Eastern-European Journal of Enterprise Technologies ISSN 1729–3774. 6/7 (114) 2021.DOI: 15587/1729–4061.2021.245885
- I. Polyakova, R. Imambayeva, B. Aubakirova, N. Shogelova, Y. Glyzno, A. Zhumagulova. Determining static characteristics of corrugated shell elements made from composite materials. DOI: 10.15587/1729–4061.2022.269399. «Eastern-European Journal of Enterprise Technologies» (№ 6/7 (120) 2022).







