В данной статье рассматриваются современные взгляды развития математического анализа и его значение в других научных дисциплинах. Проведен перекрестный и сравнительный анализ влияния методик и различных факторов на развитие математики.
Ключевые слова: анализ, метод, образование, математика, наука.
Математика — это и искусство, и наука, и в ее основе лежит чистая математика. Чистая математика исследует границу математики и чистого разума. Это было описано как «та часть математической деятельности, которая выполняется без явного или непосредственного рассмотрения прямого применения», хотя то, что «чисто» в одну эпоху, часто становится применимым позже. Финансы и криптография — современные примеры областей, в которых чистая математика применяется существенным образом.
Грубо говоря, анализ имеет дело с аппроксимацией определенных математических объектов, таких как числа или функции, другими объектами, которые легче понять или с которыми легче обращаться. Например, если вы хотите узнать первые несколько десятичных знаков числа пи, то, скорее всего, вы захотите записать число пи как предел последовательности чисел, которую вы уже знаете, как вычислить. Или пример наоборот: последовательность факториалов n! выглядит эстетично, но в расчетах часто требуется приближение n! что более четко показывает его порядок роста; такое приближение дается классической формулой Стирлинга:
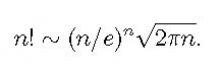
Если вы хоть немного были знакомы с исчислением, то вы уже знаете по крайней мере одну из основных идей анализа — дифференцируемые функции локально аппроксимируются линейными. Можно утверждать, что эта идея послужила реальной отправной точкой анализа около трехсот лет назад.
Но вы можете быть уверены, что анализ, который вы изучаете сегодня, выглядит совсем не так, как три (или сто) лет назад. Как и в случае с другими жизненно важными разделами математики, анализ постоянно развивался и сегодня имеет важные приложения в науке, технике и экономике. Например, финансовая отрасль стала крупным работодателем математиков из-за использования анализа.
В настоящее время анализ накопил такой огромный массив результатов, что «краткий обзор» области буквально невозможен. Основные области, представляющие интерес для аналитиков отдела чистой математики, включают реальный анализ, анализ Фурье (и вейвлеты), функциональный анализ, теорию операторов и алгебры, гармонический анализ, теорию вероятностей и теорию меры. Дифференциальные уравнения — еще одна важная область анализа, изучаемая многими прикладными математиками в Ватерлоо.
Греческие математики, такие как Евдокс и Архимед, неформально использовали концепции пределов и сходимости, когда они использовали метод исчерпывания для вычисления площади и объема областей и твердых тел.
В Индии математик XII века Бхаскара придумал дифференциальное исчисление и привел примеры производной и дифференциального коэффициента, а также формулировку того, что сейчас известно, как теорема Ролля. В 14 веке математический анализ зародился у Мадхавы в Южной Индии, который развил основные идеи разложения функции в бесконечный ряд, степенного ряда, ряда Тейлора и рациональной аппроксимации бесконечного ряда. Он разработал ряд Тейлора тригонометрических функций синуса, косинуса, тангенса и арктангенса и оценил величину ошибок, возникающих при усечении этих рядов. Он также разработал бесконечные цепные дроби, почленное интегрирование, аппроксимацию синуса и косинуса рядами Тейлора и степенные ряды радиуса, диаметра, длины окружности, π, π/4 и угла θ. Его последователи в школе Кералы еще больше расширили его работы до 16 века.
В Европе во второй половине 17 века Ньютон и Лейбниц разработали исчисление, которое под влиянием прикладной работы, продолжавшейся в 18 веке, превратилось в такие темы анализа, как вариационное исчисление, обыкновенные уравнения и уравнения в частных производных, Анализ Фурье и производящие функции. В этот период методы исчисления применялись для аппроксимации дискретных задач непрерывными.
В 18 веке Эйлер ввел понятие функции, и оно стало предметом споров среди математиков. В 19 веке Коши первым поставил исчисление на прочную логическую основу, введя понятие последовательности Коши. Он также начал формальную теорию комплексного анализа. Пуассон, Лиувилль, Фурье и другие занимались уравнениями в частных производных и гармоническим анализом.
В середине века Риман представил свою теорию интегрирования. Последняя треть XIX века была отмечена арифметизацией анализа Вейерштрассом, который считал, что геометрические рассуждения по своей сути вводят в заблуждение, и ввел определение предела «эпсилон-дельта». Затем математики начали беспокоиться о том, что они бездоказательно предполагают существование континуума действительных чисел. Затем Дедекинд построил действительные числа с помощью разрезов Дедекинда. Примерно в то же время попытки уточнить теоремы интегрирования Римана привели к изучению «размера» множества разрывов реальных функций.
Также стали создаваться «монстры» (нигде непрерывные функции, непрерывные, но нигде не дифференцируемые функции, заполняющие пространство кривые). В этом контексте Жордан разработал свою теорию меры, Кантор разработал то, что сейчас называется наивной теорией множеств, а Бэр доказал теорему Бэра о категориях. В начале 20 века исчисление было формализовано с использованием аксиоматической теории множеств. Лебег решил проблему меры, а Гильберт ввел гильбертовы пространства для решения интегральных уравнений. Идея нормированного векторного пространства витала в воздухе, и в 1920-х гг. Банах создал функциональный анализ.
Математический анализ включает в себя следующие подполя:
— Реальный анализ, строгое изучение производных и интегралов функций действительных переменных. Это включает в себя изучение последовательностей и их пределов, рядов и мер.
— Функциональный анализ изучает пространства функций и вводит такие понятия, как банаховы и гильбертовы пространства.
— Гармонический анализ имеет дело с рядами Фурье и их абстракциями.
— Комплексный анализ, изучение функций из комплексной плоскости в комплексную плоскость, которые являются комплексно дифференцируемыми.
— р -адический анализ, изучение анализа в контексте р -адических чисел, который некоторыми интересными и неожиданными особенностями отличается от своих реальных и сложных аналогов.
— Нестандартный анализ, который исследует гипердействительные числа и их функции и дает строгое рассмотрение бесконечно малых и бесконечно больших чисел. Обычно ее относят к теории моделей.
— Численный анализ, изучение алгоритмов аппроксимации задач непрерывной математики.
Под классическим анализом обычно понимают любую работу, в которой не используются методы функционального анализа, и иногда его также называют жестким анализом ; это также, естественно, относится к более традиционным темам. Изучение дифференциальных уравнений теперь используется совместно с другими областями, такими как динамические системы, хотя совпадение с «прямым» анализом велико.
Литература:
1. Бабенко, К. И. Основы численного анализа / К. И. Бабенко. — М.: Главная редакция физико-математической литературы издательства «Наука», 1986. — 744 c.
2. Бакушинский, А. Элементы высшей математики и численных методов / А. Бакушинский, В. Власов. — М.: Просвещение, 2014. — 336 c.
3. Босс, В. Лекции по математике. Том 1. Анализ. Учебное пособие / В. Босс. — М.: Либроком, 2016. — 216 c.
4. Воробьев, Н. Н. Теория рядов / Н. Н. Воробьев. — М.: Главная редакция физико-математической литературы издательства «Наука», 1986. — 408 c.
5. Гусак, А. А. Задачи и упражнения по высшей математике. Часть 2 / А. А. Гусак. — М.: Вышэйшая школа, 2013. — 384 c.







