В статье описываются формирование потребности в логическом доказательстве, а также примеры составленных задач на доказательство. Основные виды задач на доказательство, используемые в 5классе, опираясь на основные направления пропедевтической работы, описанные В. А. Далингером.
Ключевые слова: доказательство, пропедевтическая работа.
Проблема в логическом доказательстве встает при переходе учащихся в 7 класс, когда перед детьми возникает вопрос о поведении первых доказательств. Трудности появляются из-за не подготовки учащихся к доказательствам. Многие из нас считают, чтобы избежать доказательству теорем, целесообразно начинать данную работу в 5–6 классах.
Дети данного возраста (10–11 лет) уже осмысливают закономерности и связи, опираясь на восприятие. При этом важная роль учителя — познакомить детей с тем как доказывать и вовлечь их в учебную деятельность. При этом содержание должно быть таким, чтобы теоретические факты были получены эмпирическим путем.
Современные учебники содержат задания на доказательство, но их мало, в основном упражнения направлены на формирование навыка решения задач. Поэтому возникает необходимость в составлении упражнений, направленных на формирование потребности в логическом доказательстве.
Задания составленного нами комплекса опираются на основные направления пропедевтической работы, описанные В. А. Далингером
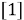
Таблица 1
В пятом классе разработаны задания по 7 темам «Простые и составные числа», «Признаки делимости», «Углы. Многоугольники», «Наибольший общий делитель (НОД) и наименьшее общее кратное (НОК)», «Умножение десятичных дробей», «Множества», «Делители и кратные».
№ 1. Тема «Простые и составные числа».
Задания:
- Найди среди рядов чисел лишний:
а) 5,7,13,19;
б) 3,23,41,53;
в) 8,10, 14,26;
г) 2,17, 61,67.
Ответ: в
2. Сравни ряд чисел и найди лишний:
а) 4,12,44,56;
б) 6,8,16,25;
в) 3,23,41,59;
г) 10,22,64,85.
Ответ: в.
- Исключи лишнее слово:
Делитель, простое число, переменная, кратное, составное число.
Ответ: переменная
- Установи закономерность и укажи недостающее число:
111931
132337
1729?
Ответ: 41 (закономерность простых чисел, следующее за 37).
№ 2. Тема «Умножение десятичных дробей»
Задания.
- Умножь числа, используя правило умножения десятичных дробей:
а) 4,367



б) 0,051



Ответьте на вопросы: чем отличается положение запятой в значении произведения от её положения в первом множителе? Сколько нулей во втором множителе?
- Вставь пропущенное число:
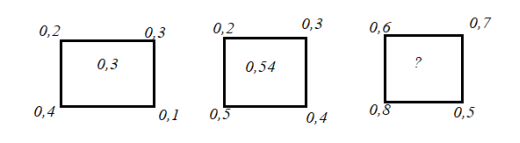
Ответ: 1,74 (
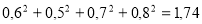
- Вставь пропущенное число

- Продолжи числовой ряд: 1,8; 2,0; 2,4; 3,2; ?
Ответ: 4,8 (
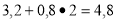
№ 3. Тема «Признаки делимости».
- Выделите в математических утверждениях условие и заключение:
а) если запись числа оканчивается на 4, то число делится на 2;
б) если запись числа оканчивается на 6, то число делится на 2;
в) если запись числа оканчивается на 0, то число делится на 2;
г) если запись числа оканчивается на 2, то оно не делится на 5;
д) число, запись которого оканчивается на 2, не делится на 5;
е) если сумма цифр числа делится на 9, то натуральное число делится на 9.
- Составьте математическое утверждение по его условию «Число, сумма цифр которого делится на 3, …»
- Составьте математическое утверждение по его заключению «….., то числа делятся на 10».
№ 4. Тема «Углы. Многоугольники»
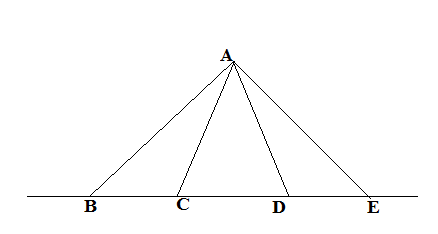
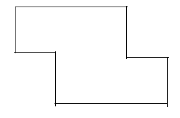
- Определи количество углов, изображенных на рисунке.
- Перечисли четырехугольники, изображенные на рисунке.
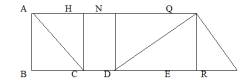
- Определи количество треугольников на рисунке.
- Сделай необходимые измерения и вычисли периметр фигуры, изображенной на рисунке.
№ 5. Тема «Множества».
- Ученики 5 класса во время летних каникул отдыхали в лагерях «Березка» и «Тамань». Из них 14 провели время в лагере «Березка», 8 — посетили лагерь «Тамань», а 5 — посетили оба лагеря. Сколько учащихся в классе?
- У 6 учащихся класса имеются набор для тенниса, а у 7 — набор для баскетбола. Из них 3 учащихся имеют набор для тенниса, но у них нет набора для баскетбола. А у 4 учащихся есть набор для баскетбола, но нет для тенниса. Сколько учащихся имеют наборы для тенниса и баскетбола? Изобрази решение задачи на кругах Эйлера-Венна.
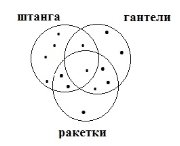
- В классе у учащихся есть бадминтон, штанга и ракетки. Используя рисунок 7, ответь на вопросы:
а) Сколько учащихся имеют бадминтон?
б) Сколько учащихся имеют штангу?
в) Сколько учащихся имеют ракетки?
г) Сколько учащихся имеют бадминтон и штангу?
д) Сколько учащихся имеют бадминтон и ракетки?
е) Сколько учащихся имеют бадминтон, штангу и ракетки?
- Из 50 студентов 40 человек владеют русским языком, 30 — английским, 10 — казахским, 15 — русским и английским языками, 5 — русским и казахским, 5 — английским и казахским. Сколько студентов владеют тремя языками?
№ 6. Тема «Наибольший общий делитель (НОД) и наименьшее общее кратное (НОК)».
- Как измениться наибольший общий делитель двух и более числе, если каждое из них уменьшить в 2 раза? (Ответ: наибольший делитель этих чисел тоже уменьшиться в два раза).
- Если несколько чисел умножить на одно и тоже число, то наибольший общий делитель данных чисел ____________. (Ответ: умножиться на это число)
- Какая связь между наибольшим общим делителем двух чисел с меньшим из данных чисел? (Ответ: наименьший общий делитель равен меньшему из данных чисел).
- Каким числом будет являться наименьший общий делитель двух чисел, если одно из них кратно другому? (Ответ: наименьший общий делитель является наименьшим числом из данных).
- Что можно сказать за наименьшее общее кратное, если числа являются взаимно простыми? (Ответ: наименьшее общее кратное равно их произведению).
- Если каждое из данных чисел умножить на одно и тоже число, то что можно сказать за НОК? (Ответ: наименьшее общее кратное тоже уменьшиться на это число).
№ 7. Тема «Делители и кратные»
-
Если 125 делится на 5, а 368 не делится на 5. Делится ли 125
-
Делится ли число
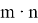
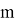

-
Если число
р
делится на
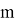
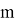
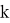
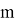
- Получен остаток 9 при делении числа в на 16. Подумай, правильно ли выполнено деление?
- Докажи, что число k кратно 7, если число k кратно 49. Обоснуй свой ответ.
- Докажи, что а кратно в , то в — делитель а . Обоснуй свой ответ.
- Докажи что число а простое, если а:1 и а:а .
- Докажи, если число является простым, то оно имеет два делителя. Обоснуй свой ответ.
- Не выполняя вычислений, докажи, что число 12 является делителем числа 24 и кратным 6.
- Обоснуй высказывание «Число 93 делитель числа 9579».
Литература:
1. Далингер В. А. Методика обучению учащихся доказательству математических предложений: кн. для учителя. — М.: Просвещение, 2006. — 256с.







