К вопросу кривой эллипса



В статье получено уравнение эллипса через длины полуосей и углов треугольника, вписанного в эллипс. При этом основание АВ треугольника АВС совпадает с осью АВ = 2а, а точка С является произвольной точкой эллипса С(Х, У). Получены также выражения координат Х, У через тригонометрические функции углов треугольника АВС.

The article obtained the equation of an ellipse in terms of the lengths of the semiaxes and angles of a triangle inscribed in it. In this case, the base AB of the triangle ABC coincides with the axis АВ = 2а, and the point C is an arbitrary point of the ellipse C (X, Y). Expressions for the coordinates X, Y are also obtained in terms of the trigonometric functions of the angles of the triangle ABC.

Зададимся целью задать уравнение эллипса через длины полуосей ( а и b или а и с ) и углов α и β полученных треугольников, соединяющих точки А(- а ; 0), В( а ; 0) и произвольную точку С( х;у ) эллипса (см. рис.1).

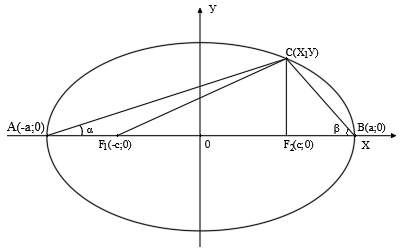
Рис. 1.

Тогда АС = , BC = , AB = 2 a , (1)

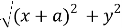
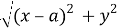
∠A = α, ∠B = β.

С другой стороны, F ₁ C + F ₂ C = 2 a

или

+ = 2 a (2)

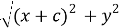
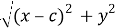
Как известно из (2), получается формула для эллипса:

+ = 1 (3)

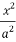
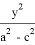
После замены а ² — с ² = b ² получается

+ = 1 (4)

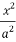
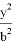
А теперь выразим х через тригонометрические функции α и β.

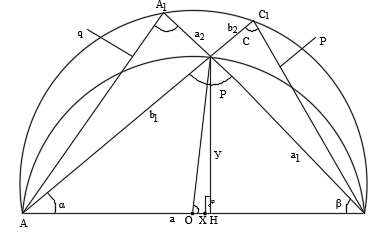
Рис. 2.

Пусть точка С находится на эллипсе, а точки А ₁ , С ₁ на окружности. Точки А ₁ , С ₁ получены пересечением соответственно сторон ВС и АС с окружностью диаметром 2 а . По теореме Пифагора для прямоугольных треугольников АА ₁ В и АС ₁ В можно написать следующие уравнения:

² = (2 ²

² = (2 ² (5)

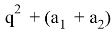
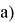
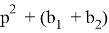
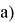
Здесь q ² = ² = ^— ( + 2

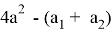
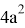
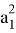
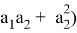
Если в последнем равенстве учесть а ₂ = - b ₁ cosγ, то получаем:

q ² = ² . Аналогичным образом получаем, что b ₂ = a ₁ cosγ

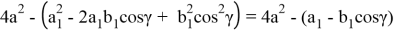
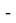
p ² = ² .

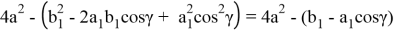
Таким образом имеем:

²

² (6)

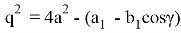
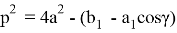
С другой стороны, из треугольников АА ₁ В и АС ₁ В можно получить зависимости q = 2 a sinβ, p = 2 a sinα. Подставляя эти выражения в (6), получаем:

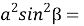
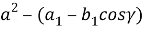
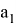
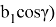
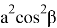
4 4 ²  (

- ² = 4

4 4 ²  ( - ² = 4 (7)

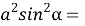
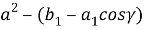
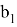
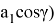
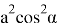
Если эти уравнения разделим друг на друга, то получим

(8)

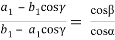
Используя теорему косинусов для треугольника АСВ, получаем

4 = (9)

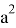
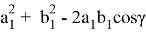
Также можно получить

² + ² -

+2 ax — (10)

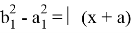
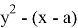
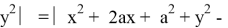
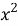
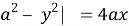
Решая систему уравнений (9) и (10), получаем:

+ 2

2

(

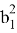
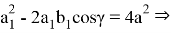
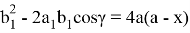
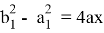
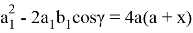
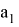
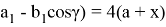
Если разделим последние два уравнения друг на друга, то получим:

(11)

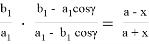
Учитывая (8) в уравнении (11), преобразуем его в следующий вид:

(12)

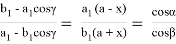
Как известно по теореме синусов:

(13)

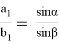
Тогда, учитывая (12), получаем

(14)

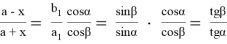
Из (14) имеем

1+

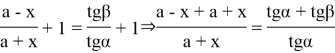
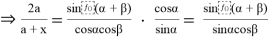
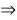
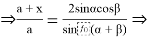
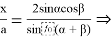
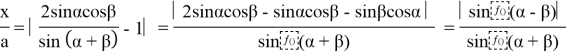
x= (15)

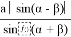
А теперь выразим y через a и углы треугольника АВС. Как видно из

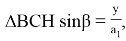
откуда у=а ₁ sin β (16)

С другой стороны, по теореме синусов:

(17)

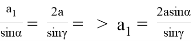
Учитывая (17) в (16), получаем

y = (18)

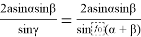
Таким образом мы в формуле эллипса =1 для переменной х получаем

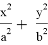
x = (19)

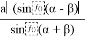
Для переменной у получаем

y =

(20)

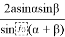
Если подставим (19) и (20) в (4), мы получаем:

β =

=

α)) =

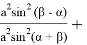
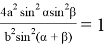
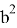
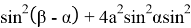
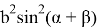
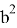
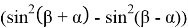
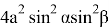
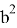
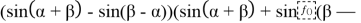
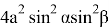
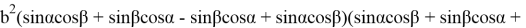
+sinβcosα sinαcosβ) =

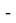
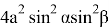
2

= (21)

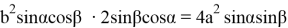
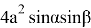
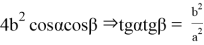
Последнее уравнение является формулой эллипса. Действительно, как видно из рис.2, tgα = .

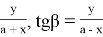
Тогда tgα tgβ = ⇒ =

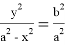
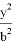
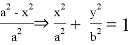
Таким образом в данной статье получены некоторые формулы, связанные с кривой эллипса.

Литература:

1. M. X. Nəsibov. Qəribə əyrilər. Elmi-kütləvi ədəbiyyat. Bakı,”Maarif” nəşriyyatı, 1985-ci il.-156 səh.
2. Овчинников А. В. Алгебра и геометрия в вопросах и задачах: Основы алгебры и аналитической геометрии. Изд. Стереотип. И RSS. 2022, 288 c. ISBN 978–5-9519–2839–9