Задача о дифракции волн в упругих телах, содержащих трещины, включения и другие дефекты, представляют значительный интерес в связи с проблемами различных областей техники. В то же время они сводятся к решению сложных краевых задач, к которым могут быть применены различные математические методы.
Рассмотрим следующую плоскую динамическую задачу теории упругости, моделирующую некоторые динамические явления, возникающие при неразрушающем ультразвуковом контроле сварных соединений.
Пусть в плоскости

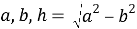
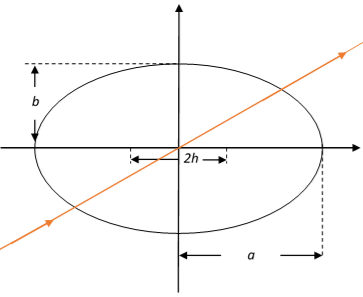
Рис. 1. Выбор декартовой системы координат
Область, занимаемую эллипсом, обозначим
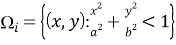
Дополнение
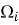
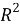

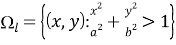
Границу между указанными областями обозначим

Предположим, что области
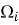

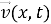
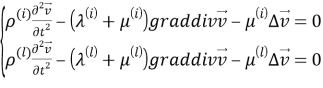
Здесь
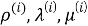
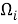
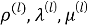
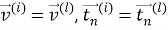
Здесь
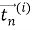
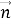
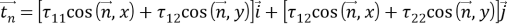
где



Введем потенциалы вектора смещений:
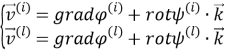
Здесь

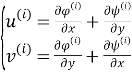
Аналогичные формулы имеют место для
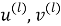
Далее компонент тензора деформаций в системе координат


Аналогичные формулы имеют место для
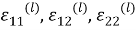
Для компонент тензора напряжений на основании закона Гука получаем:
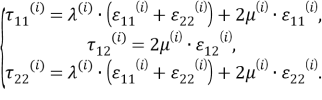
Аналогичные соотношения имеют место для
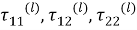
Если подставить (6) в (3), то для потенциалов
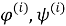
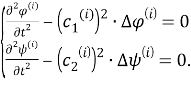
Здесь величины
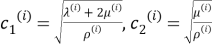
представляют собой скорости распространения продольной и поперечной волны в теле


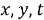
Предположим, что в направлении, указанном на рис. 1 красной стрелкой, движется некоторая заданная «падающая» волна. Она так же описывается некоторыми потенциалами
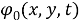
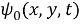
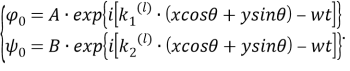
Здесь
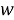
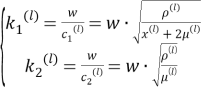
являются волновыми числами падающей волны,
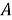

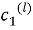

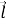


Заметим, что функции

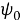
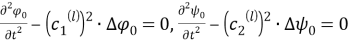
В этом легко убедиться простой подстановкой. Действительно,
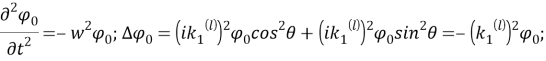

Аналогично
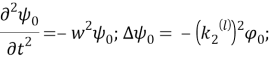
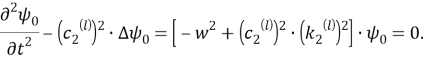
Теперь будем разыскивать

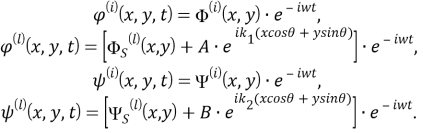
Подставляя (14) в уравнения (10) и аналогичные уравнения для
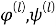
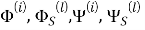
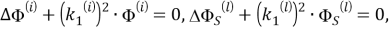
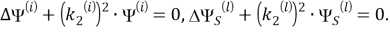
Здесь
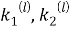
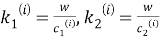
Искомые функции
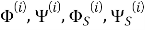
Литература:
- Самарский А. А., Николаев Е. С. Методы решения сеточных уравнений — Москва: Наука, 1978.
- Владимиров В. С. Уравнения математической физики — Москва: Наука, 1971.
- Босс, В. Лекции по математике. Том 1. Анализ. Учебное пособие / В. Босс. — М.: Либроком, 2016. — 216 c.







