Как следует из
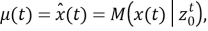
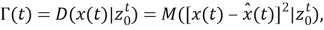
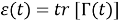
и
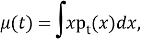
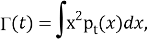
чтобы найти точность
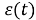
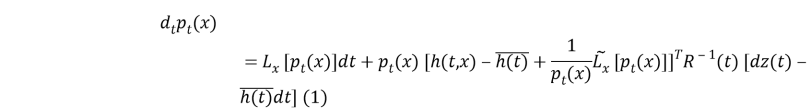
с начальным условием
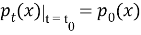
Сущность этого метода заключается в следующем. Пусть
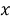
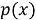
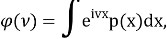
где
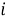
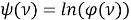
семиинвариантной функцией распределения p(x). Величины
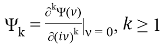
называются семиинвариантами k-го порядка и обладают тем свойством, что
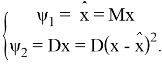
Семиинварианты порядка выше второго уже не совпадают с соответствующими центральными моментами, но быстро убывают до нуля с ростом k, если p(x) близка к гауссовой плотности. А если p(x) гауссова, то
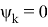
Таким образом Γ(t) может быть найдена как второй семиинвариант апостериорного распределения
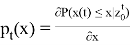
Лемма 1:
Характеристическая функция
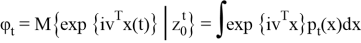
апостериорного распределения (2) удовлетворяет уравнению
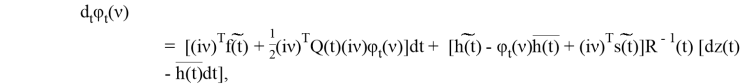
где
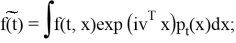
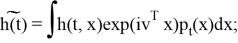
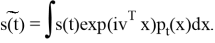
Шумы
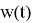
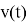
Доказательство:
Воспользуемся формулой (1) ⇒
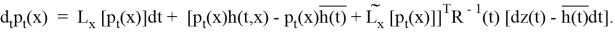
Берем преобразование Фурье от обеих частей:
слева:
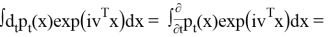
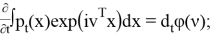
справа:
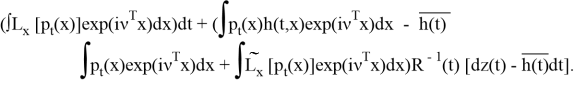
Введем обозначения, пусть
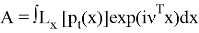
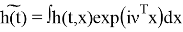
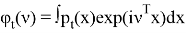
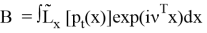
Используя то, что операторы являются сопряженными, получаем, что
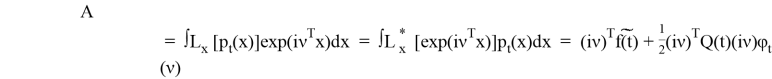
Найдем B аналогично тому, как искали A.
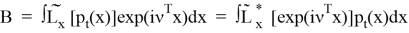
причем
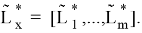
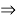
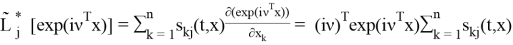
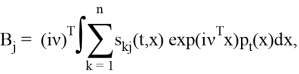
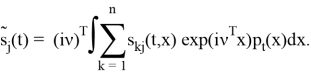
Тогда В можно записать в виде:
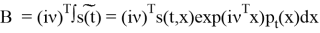
Тогда для
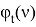
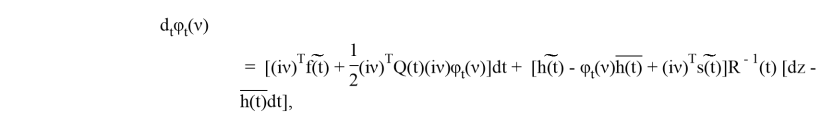
где
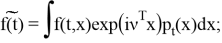
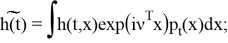
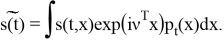
Лемма доказана.
Лемма 2:
Семиинвариантная функция
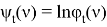
апостериорного распределения (2) удовлетворяет уравнению
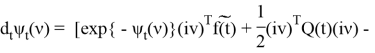
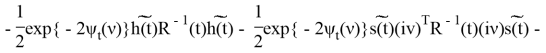
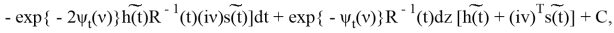
где C(t) — функция, не зависящая от
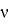
Доказательство:
Стохастически дифференцируя (4) по формуле Ито получаем, что
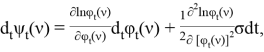
где
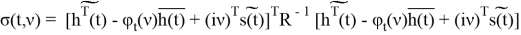
При этом нужно иметь в виду, что в качестве стохастического процесса
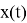
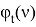
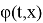
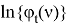
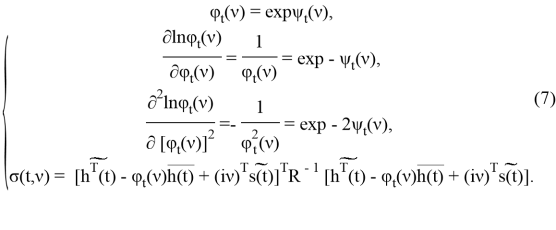
То подставляя (3) и (7) в (6), получаем после ряда алгебраических преобразований уравнение (5), где
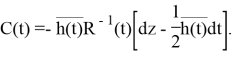
Лемма доказана.
Литература:
- Липцер Р. Ш. Статистика случайных процессов / Липцер Р. Ш., Ширяев А. Н. М.: Наука, 1974. — С. 695.
- Демин Н. С. Теория оценивания и распознавания стохастических сигналов: Учебное пособие.- Томск: Томск. ун-т, 1983. — С. 109.
- Демин Н. С. Фильтр Калмана- Бьюси для коррелированных непрерывно- дискретных наблюдений / Демин Н. С., Петров В. В. // Известия высших учебных заведений. Приборостроение. — 1978. — № 5. — С. 14–19.
- Kalman R. E. A new approach to linear filtering and prediction problems // Journal of Basic Engineering. — 1960. — № 82. С. 35–45.
- Калман Р. Е. Новые результаты в линейной фильтрации и теории предсказания /Калман Р. Е., Бьюси Р. С. // Техническая механика. — 1961. № 1. — С. 123–141.
- Пугачев В. С. Стохастические дифференциальные системы. Анализ и фильтрации/ Пугачев В. С., Синицын И. Н. — М.: Наука, 1990. — С. 630.
- Гихман И. И. Введение в теорию случайных процессов / Гихман И. И., Скороход А. В. — М.: Наука, 1977. — С. 568.
- Гихман И. И. Стохастические дифференциальные уравнения / Гихман И. И., Скороход А. В. — Киев: Наукова думка, 1968. — С. 353.







