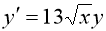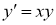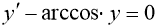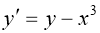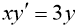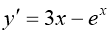Адамның үздіксіз білім алуға дайындығы мен оның әр түрлі ортада өз бетімен білім алуын қамтамасыз ету, математикалық білімін дамытуда негізгі фактор болып табылады. Бұл қажеттіліктерді жалпы мектептерде толық күйде қанағаттандыра алмайды. Алайда қызығушылықтары басқа облыста жататын оқушылардың күшті, әлсіз және барлығын ескеруге мүмкіншілік беретін сабақтан тыс қосымша математикалық білім алуды әртараптандыру қажетті. Сонымен қатар, абстрактылы математикалық түсініктің объективті шындықпен байланысы қосымша математикалық ғылымды үйренудің негізгі себебі болады.
Кілтті сөздер: факультатив курсы, факультатив сабақтар, дифференциалдық теңдеунің реті, дифференциалдық теңдеудің шешімі, изоклина
Математическое развитие является важным фактором, обеспечивающим готовность человека к непрерывному образованию и самообразованию в самых различных областях человеческой деятельности. Общеобразовательная школа не в состоянии в полной мере удовлетворить такие потребности. Однако дополнительное математическое образование учащихся в форме внеклассных занятий является необходимым условием диверсификации образования, дает возможность учитывать всех школьников, сильных, слабых и тех, чьи интересы лежат в другой области. Также важной причиной дополнительного изучения математических наук в школе является связь абстрактных математических понятий с объективной действительностью.
Ключевые слова: факультативный курс, факультативный урок, порядок дифференциального уравнения, решение дифференциального уравнения, изоклина
Қазақстан Республикасының президенті Н.Ә.Назарбаевтың Қазақстан халқына Жолдауында: «Ұлттық бәсекелестік қабілеті бірінші кезекте оның білімділік деңгейімен айқындалады. Әлемдік білім кеңістігіне толығымен кірігу білім беру жүйесін халықаралық деңгейге көтеруді талап ететіні сөзсіз» — деп көрсетілген [1].
Сондықтан, елімізді дамытудың қазіргі әлеуметтік-экономикалық, саяси жағдайлары және жоғары дамыған елдердің тәжірибесі білім берудің мазмұнын, әдістерін жаңарту және жетілдіру қажеттілігін тудыруда.
Кез келген елдегі білім беру жүйесі қоғамның экономикалық, әлеуметтік және мәдени дамуына ықпал етуге бағытталған, себебі мектеп, жоғары оқу орны болашақта қоғамның экономика, мәдениет, саяси өмірі салаларында белсенді қызмет ететін адамдарды дайындайды. Сондықтан білім берудегі негізгі буын — мектептің рөлі өте жоғары.
Қазақстан Республикасының «Білім туралы» заңында (2007 ж.) білім беру жүйесінің жеке адамды қалыптастыруға, дамытуға және кәсіби шыңдауға бағытталған рөлі атап көрсетілсе, осы заңның 41-бабында: «Педагог қызметкерлер оқушылардың мемлекеттік білім беру стандартында көзделген деңгейден төмен емес білім, білік, дағды алуын қамтамасыз етуге, жеке шығармашылық қабілеттерінің көрініп дамуы үшін жағдай жасауға міндетті» делінген [2].
Сондықтан, орта мектептің алдында тұрған негізгі міндеттердің бірі — оқушылардың шығармашылық қабілетін барынша ашып, қоғамды құрып дамытуға бар мүмкіндігін жұмсайтын қабілетті жеке тұлғаны қалыптастыру. Әрбір оқушының тұлға ретінде қалыптасып дамуына математикалық білімнің үлкен үлесі бар.
Себебі, біріншіден, математика басқа ғылымдар саласының дамуының тірегі, қызметшісі, екіншіден, математика қоршаған ортаны білудің басты көзі, үшіншіден, математика дедуктивтік құрылған ғылым болғандықтан, оқушының заңға сүйеніп, ой қорытындылауын, заңды сыйлау психологиясын қалыптастырады, төртіншіден, математика адамның рухани дамуына, ғылыми көзқарастарының қалыптасуына, логикалық ойлау қабілетінің дамуына көмектеседі.
Мектеп математикасын өмірмен байланыстыру, бұл пәнді адамдардың практикалық және техникалық іс-әрекетіне қолдану үшін мектеп математикасы мен математика ғылымын жақындастыру қажет. Бірақта мектеп математика курсының мазмұны қазіргі заманның талаптарына сай емес. Сондықтан, бұл мәселені шешу мүмкіншілігі бірі — мектепте қолданбалы математика бойынша таңдау курстарын енгізу.
Жұмыстың мақсаты: «Дифференциалдық теңдеулер пайдалуымен математикалық модельдеу» таңдау курсын құрастыру. Қазіргі кезде ғылымның барлық дерлік салаларында математикалық әдістерді қолдану қажетті шартқа айналды. Ол өмір талабынан, ғылыми-техникалық прогрестік дамуынан туындайды. Кез келген ғылымдағы обьектіні зерттеу үшін математикалық модельдеу әдісін қолданады. Математикалық модельдеу әдісі қазіргі кезде математикалық экономика, математикалық биология, математикалық лингвистика, технология, бионика, тағы да басқа ғылымдардың көптеген салаларында терең қолданылып, ғылымның дамуына зор үлесін тигізуде.
Жоғарғы кластарға математиканы оқытуда дифференциялдық теңдеулердің алатын орны және рөлі көрсетілген. Таңдау курстар — бұл кәсіптік мазмұнын толықтыратын, оқушылардың танымдық қызығушылығын қанағаттандыратын оқу жоспарының жаңа элементі болып табылады [3]. Таңдау курстардың мақсаты — оқушыларды болашақтағы кәсіптік қызметінің саласын жауапкершілікпен таңдауға дайындау және оларды жекелей оқуға бағыттау болып табылады. Таңдау курстар негізгі үш типке бөлінеді: пәндік курстар, пәнаралық элективті курстар, негізгі оқу жоспарына кірмейтін пәндер бойынша таңдау курстар.Пәндік курстардың мақсаты мектептің оқу жоспарына кіретін пәндер бойынша білімдерді тереңдету және кеңейту болып табылады. Мұндай курстарға келесі курстарды жатқызуға болады: «Математикалық анализге кіріспе», «Экономикадағы математикалық әдістер», «Математикалық жаңалықтар», «Туынды және оның қосымшалары», «Параметрлер бар есептерді шешу» және т. б. Пәнаралық элективті курстардың мақсаты — оқушылардың табиғат және қоғам туралы білімдерін интеграциялау. Мысалы: «Математика лингвистикаға көмектеседі», «Циклоида және оның практикалық қосымшалары», «Фибоначчи сандары және табиғат», «Зерттеу жұмысының негіздері» және т. б. Негізгі оқу жоспарына кірмейтін пәндер бойынша элективтік курстар психологиялық, әлеуметтік, психологиялық мәдениеттанулық, өнертану мәселелерге арналған. Мысалы: «Қазіргі әлеуметтік мәселелерге кіріспе», «Адам және адамдар қоғамының психологиясы», «Экологиядағы мәселелер», «Менеджмент және маркетингтің сұрақтары» және т. б.
Құрастырылған таңдау курсты пәндік және пәнаралық курстарға жатқызуға болады, себебі мұнда алгебра және анализ бастамаларына кіретін дифференциалдық теңдеулер бөлімі тереңдетіліп оқытылады, сонымен қатар механикада, физикада, биологияда, экономикадағы кейбір процестерді белгілі бір заңдар бойынша дифференциалдық теңдеулерге келтіріп математикалық модельдерін шешу әдістері көрсетіледі.
Сонымен, «Дифференциалдық теңдеулер пайдалуымен математикалық модельдеу» атты таңдау курстың тақырыптық жоспары 1-кестеде көрсетілген.
1 кесте
Курстың тақырыптық жоспары
|
№ |
Тақырып атауы |
Оқытуды ұйымдастырудың формалары мен сағаттар саны |
|
|
Дәріс |
Практикалық сабақтар |
||
|
І бөлімі |
|||
|
1 |
Дифференциалдық теңдеулер теориясының негізгі ұғымдар мен анықтамалар |
1 |
1 |
|
2 |
Айнымалылары бөлектенетін дифференциалдық теңдеулер |
1 |
1 |
|
3 |
Бірінші ретті сызықтық дифференциалдық теңдеулер |
1 |
2 |
|
4 |
Бернулли теңдеуі |
1 |
2 |
|
5 |
Тұрақты коэффициентті екінші ретті сызықтық біртекті дифференциалдық теңдеулер |
2 |
2 |
|
6 |
Коши есебі |
1 |
1 |
|
Бақылау жұмыс № 1 |
1 |
||
|
ІІ бөлімі |
|||
|
7 |
Математикалық модельдеудің этаптары мен принциптері |
2 |
|
|
8 |
Механикалық тербелістер |
2 |
2 |
|
9 |
Электрлік тербелістер |
2 |
2 |
|
10 |
Биологияда математикалық модельдері |
2 |
2 |
|
11 |
Экономикадағы математикалық модельдері |
2 |
2 |
|
Бақылау жұмыс № 2 |
1 |
||
|
Барлығы |
17 |
19 |
|
2.1.2 Тақырыптар бойынша теориялық материалдары мен практикалық тапсырмалары
Тақырып 1: Дифференциалдық теңдеулер теориясының негізгі ұғымдар мен анықтамалар.
Жоспар
- Негізгі ұғымдар мен анықтамалар.
- Бағыттар өрісі.
- Бірінші ретті дифференциалдық теңдеулердің геометриялық мағынасы.
- Практикалық тапсырмалары
Теориялық мәліметтер
1. Негізгі ұғымдар мен анықтамалар.
Анықтама.Тәуелсіз айнымалы
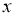
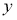
Дифференциалдық теңдеунің реті деп сол теңдеуге кіретін туындының ең үлкенін атайды.
Мысалы:
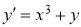
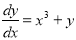
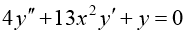
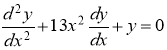
Бірінші ретті туындысы арқылы айқындалған дифференциалдық теңдеу былай беріледі
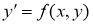
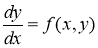
мұнда
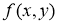
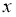
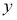
(2.1) теңдеуін алып, түрлендірулер жасайық
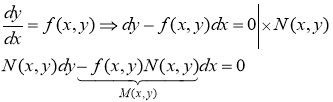
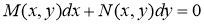
симметриялық түрде берілген бірінші ретті жай дифференциалдық теңдеу болады.
Анықтама.Кейбір
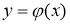
Мысалы:
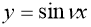
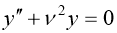
Шешімі:
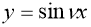
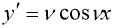
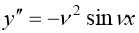
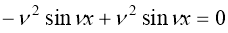
тепе-теңдік алдық, яғни, расында да,
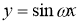
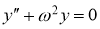
- Бағыттар өрісі.
Егер
Сур.1. Бағыттар өрісі
Мысалы, егер
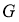
Бағыттар өрісін көрсету үшін
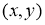
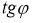
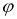
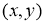
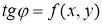
теңдеуі арқылы анықталады. Егер
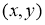
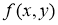
3. Бірінші ретті дифференциалдық теңдеулердің геометриялық мағынасы.
Жалпы (2.1) теңдеуді шешімін табу процесін оны интегралдау деп атайды, ал шешімінің
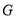
Айталық,
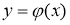
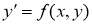
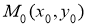
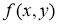
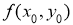

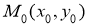
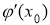
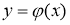
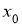
Анықтама. Егер интегралдық қисықтың әрбір нүктесінде (2.1) теңдеумен анықталатын өрістің көлбеу бағыты әрқашанда бірдей болса, онда оны изоклинадеп атайды.
Изоклинаның теңдеуі
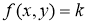
мұнда
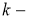
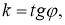
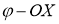
Изоклина (2.1) теңдеудің шешімін аналитикалық түрде таппай-ақ, оның интегралдық қисығының бейнесін алуға мүмкіндік береді (2-суретте изоклиналар көрсетілген).
Мысалы: Изоклина арқылы
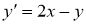
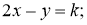
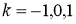
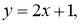
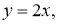
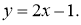
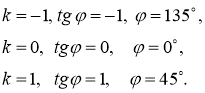
Осы зерттеулер берілген теңдеуді интегралдық қисықтарын жуықтап салуға мүмкіндік береді және бұл қисық 2 сурете бейнеленген
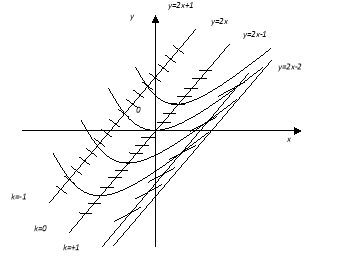
Сур. 2. Изоклиналар
4.Практикалық тапсырмалары
Тапсырма 1.
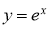
Тапсырма 2. Изоклина арқылы келесі теңдеулердің интегралдық қисықтарын жуықтап салу керек [1]
Таңдау курстың жалпы көлемі 36 сағаттан тұрады, оның ішінде 17 дәріс сабақтары, 17 практикалық сабақтары және 2 сағат бақылау жұмыстары. Әр тақырып бойынша дәріс тезистері жазылып, практикалық сабақтардың тапсырмалары құрастырылған. Бақылау жұмыстары жеке-жеке тесттен және бір тапсырмадан тұрады [4–9]. Таңдау курсты құру барысында оқушының деңгейі есепке алынды. Құрастырылған «Дифференциалдық теңдеулер пайдалуымен математикалық модельдеу» атты таңдау курсты мұғалімдерге 11 сыныптың 3 тоқсанда өткізуіне ұсынылады.
Әдебиет:
- ҚР-сының Президенті Н.Назарбаевтың Қазақстан халқына Жолдауы: «Қазакстан экономикалық, әлеуметтік және саяси жедел жаңару жолында». — Астана, 18 ақпан, 2005.
- Қазақстан Республикасның 2007 жылғы 27 шілдедегі № 319 Заңы. 41-бап. Білім беру ұйымының жарғысы.
- Колягин Ю. М. Профильная дифференциация обучения математике // Математика в школе. — 1990. — № 4. — С. 26–28.
- Сүлейменов Ж. Дифференциалдық теңдеулер курсы: оқулық. — Алматы: Қазақ университеті, 2009. — 440 б.
- Сматов Т. С. Жай дифференциалдық теңдеулер курсы (интегралдау әдістері). — Қарағанды: ҚарМУ, 2006. — 231 с.
- Әбдіманапов С., Сматов Т. С. Дифференциалдық теңдеулер курсы. — Астана: «Нұржол», 2004. — 246 с.
- Краснов М. Л., Киселев А. И., Макаренко Г. И. Обыкновенные дифференциальные уравнения: задачи и примеры с подробными решениями. — М.: Едиториал УССР, 2002. — 256 с.
- Серовайский С. Я. Математическое моделирование. — Алматы: Қазақ университеті, 2000. — 345 с.
- Филиппов А. Ф. Сборник задач по дифференциальным уравнениям. — М.: Интеграл-Пресс, 1998. — 208 с.
- Краснов М. Л., Киселев А. И., Макаренко Г. И. Обыкновенные дифференциальные уравнения: задачи и примеры с подробными решениями. –
- Сматов Т. С. Жай дифференциалдық теңдеулер курсы (интегралдау әдістері). — Қарағанды: ҚарМУ, 2006.-231 с.
- Лефшец С. Геометрическая теория дифференциялных уравнений. — М.:ИЛ.,1961. — 175 с.
- Арнольд В. И. Обыкновенные дифференциальные уравнение. –М.: Наука, 1975. — 196 с.
- Михлин С. Г. Ленейные уравнения в частных производных.–М.:ВШ,1977. — 95 с.