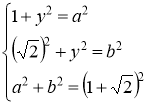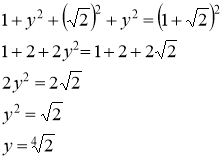Салу есептері бұл тек қана сызғыш және циркуль көмегімен геометриялық объекттерді тұрғызу. Адамның үздіксіз білім алуға дайындығы мен оның әр түрлі ортада өз бетімен білім алуын қамтамасыз ету, математикалық білімін дамытуда негізгі фактор болып табылады. Бұл қажеттіліктерді жалпы мектептерде толық күйде қанағаттандыра алмайды. Алайда қызығушылықтары басқа облыста жататын оқушылардың күшті, әлсіз және барлығын ескеруге мүмкіншілік беретін сабақтан тыс қосымша математикалық білім алуды әртараптандыру қажетті. Сонымен қатар, абстрактылы математикалық түсініктің объективті шындықпен байланысы қосымша математикалық ғылымды үйренудің негізгі себебі болады.
Кілтті сөздер: мектеп геометриясындағы салу есептері, рационал коэффициент, көпмүшелер теориясы
Задача на построение — это задача, в которой требуется построить геометрический объект, пользуясь только двумя инстрментами: циркулем и линейкой. Математическое развитие является важным фактором, обеспечивающим готовность человека к непрерывному образованию и самообразованию в самых различных областях человеческой деятельности. Общеобразовательная школа не в состоянии в полной мере удовлетворить такие потребности. Однако дополнительное математическое образование учащихся в форме внеклассных занятий является необходимым условием диверсификации образования, дает возможность учитывать всех школьников, сильных, слабых и тех, чьи интересы лежат в другой области. Также важной причиной дополнительного изучения математических наук в школе является связь абстрактных математических понятий с объективной действительностью.
Ключевые слова: задача на построение, многочленов с рациональными коэффициентами, построения задач школьной геометрии.
Геометриялық салу есептері — геометрияның міндетті тарауларының бірі болып саналады. Мектеп геометрия курсында теориялық материалдарды баяндауда салу есептері үлкен мәнге ие. Өйткені олар геометрия курсында оқытылған геометриялық образдардың арасындағы шынайы қатынастарды аңғаруға мүмкіндік береді. Бұл мақаланың мақсаты жоғарғы мектеп оқулықтарында берілген геометриялық салу есептерін беру әдістемелерін зерттеу және рационал көпмүшелер теориясы тұрғысынан геометриялық салу есептерін шығару әдістемесін ұсыну.
Біздің э.д VII ғасырдан VIII ғасырға дейінгі уақыт аралығында грек ғалымдары геометрия саласында, нақтырақ айтқанда салу есептері жөнінде аса көп мәліметтер қорын жинап, оларды өңдеді. Салу есептерінде ескеретін жағдай: салу жұмысын орындағанда тек сызғыш пен циркуль пайдаланып, басқа аспаптар қолданылмағанда ғана мұндай салуды ежелгі грек ғалымдары геометриялық салу деп есептеген. Ал егер салу жұмысын орындағанда басқа құралдар, мысалы сызбалық үшбұрыш, бөліктері бар сызғыш қолданылса, онда мұндай шешуді геометрилық салу есептері деп есептемеген.
Кесіндіні қақ бөлудің біздің оқулықтарда көрсетілген тәсілі Прокл (410–485ж.) жазбаларында баяндалған, Евклидтің атақты «Бастамаларында» салу есептерін қарастыруға үлкен орын берілген. Оның 13 кітабында көптеген салу есептері қарастырылған, олардың бірсыпырасы орта мектепте қазірде де қарастырылады. Евклид «Бастамаларының» бірінші кітабында үшбұрыштарды салу тақырыбы енгізілген. Оның төртінші кітабында басқа мәселелермен бірге, дұрыс төртбұрышты, бесбұрышты, алтыбұрышты және онбесбұрышты салу мәселелері қарастырылған. Әсіресе бұрышты тең үш бөлікке бөлу (бұрыш трисекциясы) туралы есепке көп еңбек еткен. Алайда бұл есепті шешуге арналған барлық еңбек зая кетті. Бұл есепті тек сызғыш пен циркульді қолданып шешуге болмайтындығы қазіргі уақытта дәлелденді.
Циркуль мен сызғышты пайдаланып салуға болмайтын есептерді шешуге геометриялық алгебра жарамсыз болды. Көп ұзамай осындай есептердің көп екендігі анықталды. Солардың ішінен математиканың ұзақ тарихи жолында сарапқа салынып, математиканың дамуына үлкен ықпал жасаған үш есепке тоқталайық.
- Кубты екі еселеу есебі- көлемі берілген кубтың көлемінен екі есе үлкен куб салу керек.
- Бұрышты трисекциялау есебі -берілген бұрышты тең үшке бөлу.
- Дөңгелекті квадраттау есебі -берілген дөңгелекке тең аудандас квадрат салу.
Енді осы үш салынбайтын есепке аздап тоқталсақ. Ол үшін бізге алдымен теорема беруіміз керек.
Теорема.
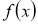
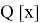
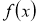
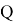
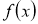
Бұл теореманың негізгі мақсаты, Мысалыға
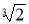
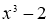
Кубтың көлемін екі еселеп салу
.
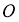
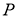
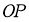
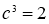
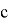
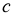
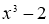
Кез келген бұрышты үшке бөлу.
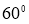
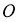
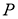
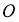
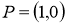
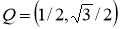
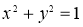
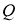
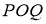
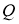
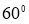
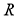
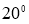
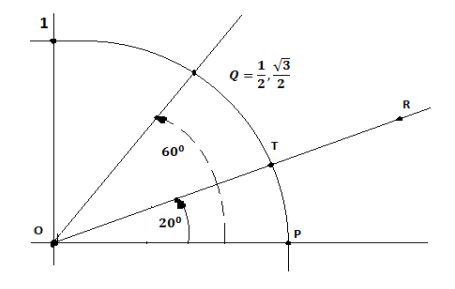
1-сурет
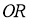
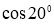
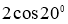
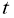
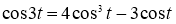
Егер
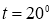
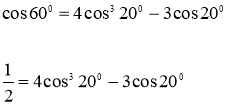
Теңдіктің екі жағында 2 көбейтеміз, сонда бізде келесі түрдегі теңдік шығады:

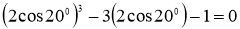
Сонымен
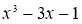

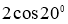
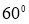
Теорема.
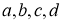
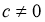
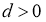
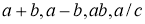
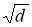
Дәлелдеуі.
Біз бірінші
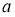
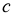
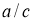
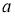
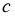
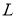
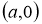
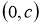
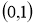
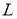
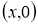
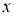
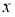
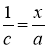
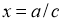
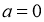
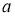
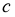
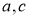
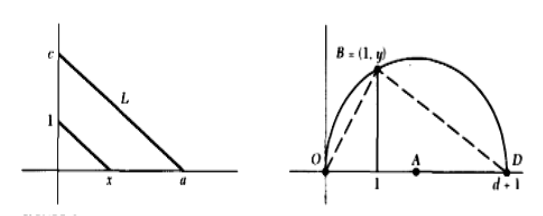
2-сурет
Егер
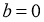
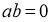
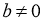
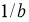
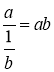
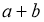
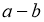
1-жаттығу бойынша
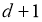
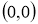
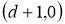
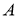
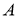
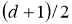
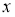
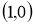
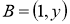
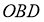
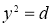
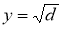
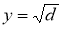
Салдар 2.2. Әрбір рационал сан конструктивті болады.
Дәлелдеуі. Әрбір бүтін сан конструктивті болады (Жаттығу 3). Сондықтан әрбір екі бүтін санның бөлшегі (рационал сандар) бойынша конструктивті болады.
Геометриялық салуларға әртүрлі мысалдар мен жаттығулар.
1.
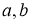
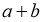
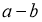
Дәлелдеудің әдісін көрсету үшін біз
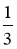
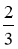
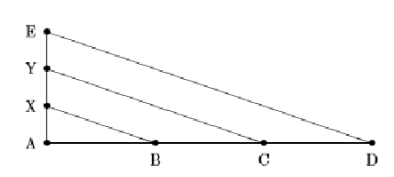
3-сурет
1
қадам.
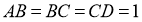
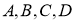
2 қадам.
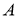
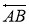
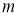
3 қадам.
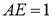
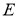
4 қадам.
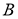
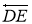
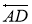
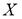
5 қадам.
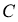
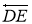
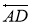
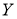
6 қадам.
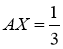
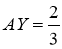
3. Кез келген бүтін сан конструктивті болатынын дәлелде.
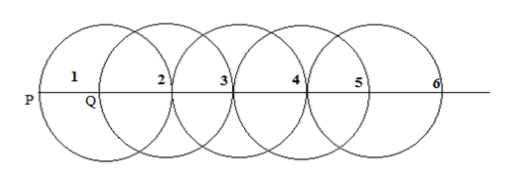
4-сурет
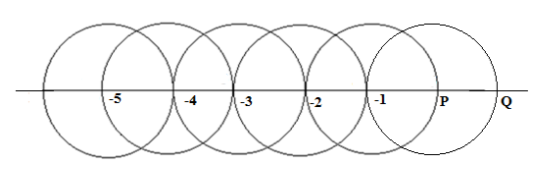
5-сурет
Біз өлшемі 1-ге тең кесінді салып, яғни
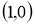
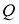
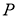
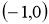
4. Егер
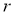
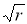
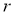
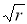
1-қадам.
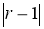
2-қадам.
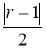
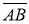
3-қадам.
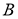
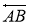
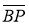
4-қадам.
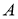
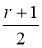
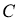
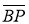
5-қадам.
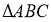
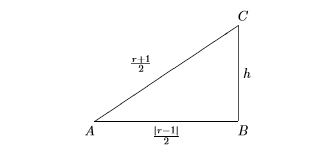
6-cурет
6-қадам. Пифагор теоремасы бойынша.
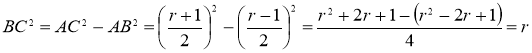
7-
қадам.
Осылайша
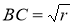
5.
Бірлік кесіндіден бастап циркуль мен сызғыш көмегімен
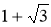
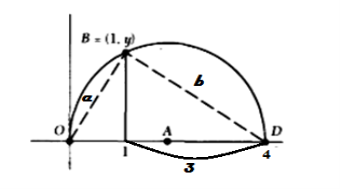
7-сурет
Біз бұл ұзындықты салу үшін
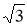
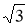
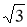
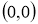
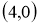
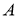
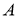
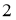
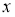
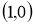
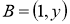
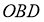

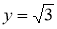
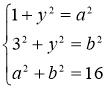
Енді жүйеге қосу амалын орындап, теңестірсек келесі теңдеуге келеміз,
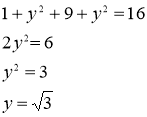
Осыдан
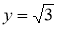
6.
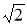
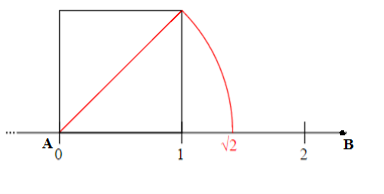
8-сурет
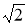
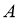
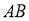
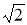
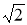
Енді жоғарыдағы есептен екінің кез келген түбір дәрежесі конструктивті ме? -деген сұрақ туады.
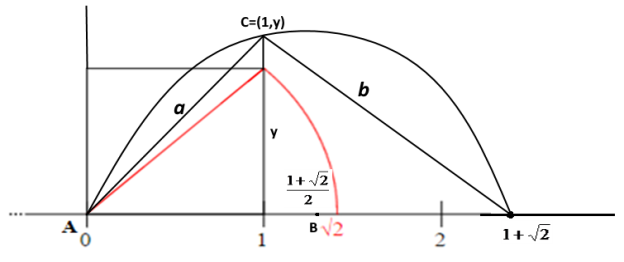
9-сурет