Комбинаторлық есептерді шешуді оқытудың ерекшеліктері негізгі мектептегі графикалық әдіс және олимпиадалық тапсырмаларды таңдау зерттеу тақырыбы. Ғылым мен практикада жиі кездесетін міндеттер бар, оларды шешу біреуіне немесе екіншісіне бағынатын әртүрлі комбинацияларды жасау керек берілген объектілерден және комбинациялардың санын санау. Мұндай тапсырмалар комбинаторлық есептер деп аталды. Комбинаторлық шешім міндеттер үлкен даму мүмкіндіктерін қамтиды: олардың негізінде ақыл-ой іс-әрекетінің әдістері жетілдірілуде, маңыздысы қалыптасуда адам үшін біріктіру қабілеті.
Кілтті сөздер: факультатив курсы, факультатив сабақтар, комбинаторлық есептердің түрлері, комбинаторлық есептерді шешімі, графтар теориясы.
Эта работа является выявлением методических особенностей обучения решению комбинаторных задач с применением графического способа в основной школе с подбором олимпиадных задач по теме исследования. В науке и практике часто встречаются задачи, решая которые, приходится составлять различные комбинации, подчиненные тем или другим условиям из заданных объектов и подсчитывать число комбинаций. Такие задачи получили название комбинаторных задач. Решение комбинаторных задач таит в себе большие развивающие возможности: на их основе совершенствуются приемы умственной деятельности, формируется важная для человека способность комбинировать.
Ключевые слова: факультативный курс, факультативный урок, виды комбинаторных задач, решение комбинаторных задач, теория графов.
Белгілі бір шарттарды қанағаттандыратын неше түрлі конфигурациялар берілген объектілерден тұруы мүмкін деген сұрақты зерттейтін математика саласы комбинаторика деп аталады.
Күнделікті өмірде бір емес, бірнеше шешімі бар мәселелер жиі туындайды. Дұрыс таңдау жасау үшін олардың ешқайсысын жіберіп алмау өте маңызды. Мұны істеу үшін біз барлық мүмкін нұсқаларды санай білуіміз керек, немесе кем дегенде олардың осы санын санауымыз керек. Мұндай есептер комбинаторлық есептер деп аталады.
Комбинаторлық есептер дегеніміз — объектілердің белгілі комбинацияларымен айналысатын тапсырмалар.
Комбинаторика- дискретті объектілерді, жиындарды және олардың арасындағы қатынастарды зерттейтін математиканың бір бөлімі. Комбинаторика математиканың көп салаларымен –алгебрамен, геометриямен, ықтималдықтар теориясымен тығыз байланысты және генетика, информатика, статистикалық физика облыстарында кеңінен қолданылады. «Комбинаторика» терминін 1666 жылы Лейбниц енгізген.
Теориялық зерттеу тұрғысынан алғанда комбинаторика алғаш рет ХVII ғасырдағы Паскаль, Ферма, Лейбниц және ХVIIІ ғасырдағы Я.Бернулли, Эйлер еңбектерінде қарастырылған. Ұлы математиктердің бұл шығармаларында комбинаторкалардың кездесуі бір жағынан алғанда тұрмыстың сан алуан мұқтаждықтарына байланысты болса, ал екінші жағынан алғанда, математиканың өз ішіндегі дамуларымен ұштасып жатыр.
Қазіргі кезде комбинаторика математика салаларының ішінде өте жедел дамып отырған бөлігіне айналды. Бұған себеп болып отырған бұл теорияның электрондық есептегіш машиналарға, информация мен ықтималдықтар теорияларына кеңінен қолданылуы. Дискреттік деп аталып жүрген математиканың өзінде де көп ықпалын тигізген, міне, осы қосылыстар теориясы. Шешуі: «нешеу», «неше тәсілмен» деген сұрақтарға жауап беруді қажет ететін есептер комбинаторлық есептер делінеді. Мұндай есептерді шешумен айналысатын математика саласы комбинаторика деп аталады.
Кейінгі жылдары комбинаториканың практикада кең қолданыс табуына электрондық есептегіш техниканың дамуы шектеулі математика рөлінің артуы, ыктималдықтар теориясы мен математикалық статистиканың практикалық маңызының күннен-күнге артуы негізгі себеп болып отыр.
Кейбір комбинаторикалық есептермен ежелгі грек математиктері де айналысқан. Дегенмен бұл саладағы маңызды нәтижелерді алгебра мен ықтималдықтар теориясының дамуына байланысты XVII және XVIII ғасыр математиктері ала бастаған. Алғашында ықтималдықтар теориясы, негізінен, құмар ойындардың (ойын сүйегін тастау, карта ойындары және т. с.с) мұқтаждығынан туындаған.
Графтар теориясы арқылы комбинаторлық есептерді шешудің әдісі.
Комбинаторика, ықтималдық теориясы, статистика элементтерін математиканы оқыту практикасына енгізу үшін нақты жағдайлар жасалынуда. Жалпы білім беретін метептерде комбинаторика, статистика және ықтималдық теориясының элементтерін оқу процесіне енгізуге мүмкіндік беретін оқу- әдістемелік қамтамасыз ету бар.
Оқу құралдарын талдай келе, мектеп оқушыларына комбинаторлық есептерді шешудің, графтар теориясы арқылы шешудің әдісі қолдану ұсынылады деген қорытындыға келуге болады. Осы комбинаторлық есептерді шешудің әдістерін толығырақ атап өтейік. Ең бірінші графтар теориясына анықтама беріп алайық.
Графтар теориясы туралы алғашқы еңбекті Л.Эйлер 1773 жылы жазған. Бірақ 1936 жылы «граф» ұғымын тұңғыш рет венгр математигі Денеш Кенинг енгізген.
Графтар теориясы-графтардың қасиетін оқыттатын дискретті математиканың бір бөліміне жатады.
Графтар ғылымда да практикада да түрлі салаларда математикалық модельдердің маңызды элементтері болып табылады. Графтар көмегімен автоматика, электроника, физика, химия сияқты білім аймақтарында жинақталған мәселелерді шешуді жеңілдетеді. Графтың көмегімен жол, газ құбырлары, жылу және электр желілерінің сұлбалары кескінделеді. Сонымен қатар математикалық экономикалық есептерді шешуде үлкен маңызға ие. Геоақпараттық жүйелерде де қолданылады. Жаңадан жоспарланған немесе белгілі бір үйді қайта жоспарлаужа,құрылыстарда,нысандарда ол төбелері ретінде қарастырылса, олардың жолдарының бірігуін, инженерлік желілер және басқалары-оның қабырғасы ретінде қарастырылады. Сонымен қатар,ең қысқа айналу жолын немесе белгілі бір көзделген жерге ең жақын яғни ең қысқа жолды табу сияқты графтардан шығатын түрлі есептеулерді қолдану тиімді жоспарлауға мүмкіндік береді.
Граф анықтамасын қарапайым сөзбен түсіндірсек-нүктелер жиынынан (графтың төбелері) тұратын және осы нүктелер жиынын қосатын түзу не қисық кесінділерден (граф қабырғалары) тұратын сұлбаны айтамыз. Граф G=(V,E) екі жиыннан, яғни шекті жиындар элементтерінен тұрады.
Бұл жерде G-граф, ал V-графтың төбелері, E-графтың қабырғалары деп аламыз.
Графтың төбелерінің қандай сызықтарымен қосылатындығы (түзу әлде қисық), сызықтардың ұзындығы туралы ақпараттар маңызды емес.Төбелердің арасында байланыс бар екендігі және ол байланыс туралы ақпарат R доғалар жиынында екендігі болса болды.Төбелерді қосатын сызықтардың бағыты көрсетілген болуы мүмкін (мысалдағы сияқты). Мұндай граф бағытталған граф деп аталады (орграф).
Көбінесе өмірде және тәжірибеде мәселенің бір емес, бірнеше шешімдері бар кездер туындайды. Олар салыстыруды қажет етеді, содан кейін белгілі бір жағдайға ең қолайлысын таңдау керек. Комбинаторлық есептерді шешу үшін элементтердің кез-келген комбинациясын жоғалту мүмкіндігін жоққа шығаратын әртүрлі құралдар бар:
- Ықтимал шешімдер ағашын тұрғызу әдісі.
- Кестелеу әдісі.
- Граф схеманы құру әдісі.
Есептерді шешу кезінде әртүрлі комбинацияларды таңдай отырып, шатасуымыз мүмкін. Бұл жағдайда ықтимал шешімдер ағашын құру әдісі көмекке келеді. Сыртқы жағынан мұндай схема ағашқа ұқсайды, демек, аты- ықтимал нұсқалардың ағашы. Ағаштың дұрыс құрылысымен ықтимал шешімдердің ешқайсысы жоғалмайды.
Графтардың қарапайым және маңызды типтері бар. Бірақ оған барлық авторлар бірдей- ағаш деген атау берген. Ағаштар ғылымның көп саласында қолданылады. Сонымен қатар, графтар теориясында да ерекше орын алады. Қандай да болмасын графтар туралы есептерді шешу барысында, ол есептерді ең алдымен ағаштарда зерттейді.
Ағаш түсінігінің бірнеше анықтамасы бар. Мысалы ағаш дегеніміз- бір ғана қисынды компоненттен тұратын орман немесе бұл циклдары жоқ графтар.
Төбенің әрбір жұбын байланыстыратын бір ғана тізбегі бар байланысқан графтар ағаштар деп аталады. Сонымен қатар циклдері жоқ байланысқан графтар да ағаштарға жатады.
Тізімдеу үшін жиі белгілерді енгізу қажет. Мысалы мәселе қызыл және жасыл шарлар туралы болса, онда бұл шарларды салу немесе олардың түстерін толық жазу қажет емес. Сіз тек бірінші әріптермен шектеле аласыз — Қ және Ж».
Объектілерді таңбаларымен ауыстыру кодтау деп аталады.
Есеп 1.7
1, 4 және 7 сандарын пайдаланып неше екі таңбалы сан жасауға болады?.
Шешуі. Сандардан құрастыруға болатын барлық екі таңбалы сандарды жазуымыз керек: 1,4 және 7. Сандардың ешқайсысын жіберіп алмау немесе қайталамау үшін сандарды өсу ретімен жазамыз. Екі таңбалы сандарды 1 санынан, содан кейін 4 санынан, содан кейін 7 санынан жаза бастаймыз. Нәтижесінде екі таңбалы сандар шығады: 11,14,17,41,44,47,71,74,77.
Осылайша, осы үш саннан тек 9 түрлі екі таңбалы сандарды жасауға болады.
1, 4 және 7 сандарынан екі таңбалы сандарды құрастыру мәселесіне қайта оралайық.Оны шешу үшін арнайы схема құрастыруға болады.
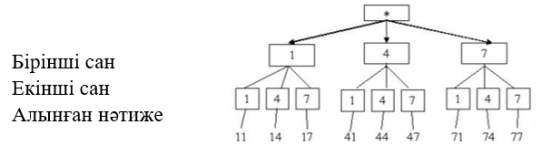
6 сур. 1.7-есептің мүмкін болатын шешімдер ағашы
Бұл схема шын мәнінде ағашқа ұқсас, тек «төңкерілген» және діңі жоқ. «*» белгісі ағаштың түбірін білдіреді, ал әртүрлі шешімдер ағаштың бұтақтары болып табылады. Екі таңбалы санды алу үшін алдымен оның бірінші цифрын анықтау керек. Бірінші сан болуы мүмкін: 1,4 немесе 7, яғни бізде үш нұсқа бар. Сондықтан «*» нүктесінен үш кесінді сызып, ұштарына 1,4 және 7 сандарын орналастырамыз.
Содан кейін біз екіншісін таңдауымыз керек, тағы да үш таңдауымыз бар: 1,4 немесе 7. Бұл опцияларды ағашта көрсету үшін бірінші саннан тағы үш кесінді сызып, 1,4 және 7 сандарын жазамыз. әрқайсысының соңында.Нәтижесінде алынған екі таңбалы сандарды кесінділер бойынша жинаймыз, біз 9 екі таңбалы сандарды жасай алдық. Айта кету керек, бұл сандардан басқа екі таңбалы сандарды құрастыру мүмкін емес.
Жауабы: 9
Есеп 1.8
Сыныпта жақсы пианино тартатын үш адам бар, қалған екеуі гитарада ойнайды, тағы біреуі фортепианода ойнай алады. 24 пианист, гитарист және фортепианошы тұратын концерттік топты неше тәсілмен құра алады?.
Шешуі.
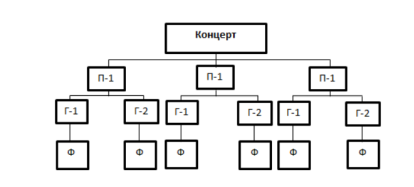
2 сур. Мүмкін нұсқалары ағашы
Сонымен, концертті құрастырудың 6 нұсқасы бар.
Жауабы: 6
Кестелерді құрастыру.
Комбинациялық есептерді кестелер арқылы шешуге болады. Кестелер берілген есепті шешудің барлық нұсқаларын, сондай-ақ ықтимал нұсқалар ағашын анық көрсетеді.
Есеп 1.9
1,3,4,6,7,8,9 сандарынан неше тақ екі таңбалы сан жасауға болады?. [15].
Шешуі . Кесте құрайық: сол жақта бірінші бағанда іздеген сандардың бірінші цифрлары, жоғарғы жағында бірінші қатарда екінші цифрлар.
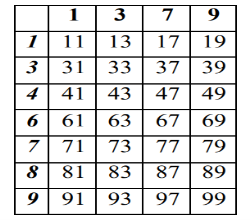
Жауабы: 28
3 сур. 1.9-есептің мүмкін нұсқаларын санау
Граф-схеманы құру
Барлығы метро станцияларының, трамвай жолдарының схемасын немесе теміржол қатынастарының картасын көрді. Нүктелер — оларды байланыстыратын қалалар, сегменттер немесе доғалар-теміржолдар. Мұндай схемалар графтар деп аталады.
Бұл элементтердің барлық комбинацияларын олардың саны аз болған кезде сұрыптау және есептеу қиын емес. Үш немесе одан да көп элементтердің комбинацияларын құру және есептеу қажет болған жағдайда олар көбінесе графтық сызбаларды қолданады.
Сонымен, егер кеңістіктің еркін нүктелері сегменттермен немесе доғалармен өзара байланысты болса (бәрі бірдей емес), онда мұндай байланыс (схема) граф деп аталады.
Граф-бұл нүктелерден (графтың жоғарғы жағы) және оларды байланыстыратын сызықтардан (графтың шеттері) тұратын геометриялық фигура.
Сонымен қатар, шыңдардың көмегімен белгілі бір жиынтықтың элементтері (заттар, адамдар және т. б.), ал жиектердің көмегімен элементтер арасындағы белгілі бір байланыстар бейнеленген. Мәселенің шарттарын суреттеуге ыңғайлы болу үшін графтың шыңдарын шеңберлермен немесе тіктөртбұрыштармен ауыстыруға болады.
Есеп 1.1 0
Саябақта 4 тоған бар. Бір тоғаннан екіншісіне ең қысқа жолмен бару үшін олардың арасындағы жолдарды құммен толтыру туралы шешім қабылданды, яғни. айналып өтудің қажеті жоқ еді. Тапсырма: қандай жолдарды орындау керектігін көрсетіңіз?

4 сур. Тапсырма шарты бойынша төрт тоған
Жауабы: 6
Есеп 1.11
Жансерік, Ғалымжан, Оралбек, Данияр және Мұхит спортзалға жиналды. Жігіттердің әрқайсысы басқа екеуін ғана таниды. Кім-кімді таниды?
Шешуі.
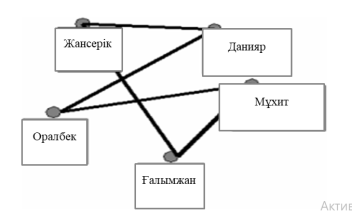
5 сур. 1.11 есептің толық графы
Жауабы : Жансерік Ғалымжан мен Даниярды, Данияр Жансерік пен Оралбекті, Оралбек Данияр мен Мұхитті, Мұхит Оралбек пен Ғалымжанды, Ғалымжан Оралбек пен Мұхитты таниды.
Сонымен, әртүрлі авторлардың математика және алгебра бойынша әртүрлі оқулықтарын талдай келе, бұл тақырыпқа бағдарламада аз ғана сағат берілгенін байқаймыз. Әр түрлі сыныптардан «Комбинаторлық есептерді графтар теориясы арқылы шешу» тақырыбымен танысу. Шешудің графтар теориясына мыналар жатады: мүмкін болатын нұсқалар ағашын құрастыру, кестелерді құрастыру, граф диаграммасын құру. Негізінен, оқулықтардың авторлары оны қолдану мысалдарымен ықтимал нұсқалар ағашын құрастыру әдісін зерттеуді тоқтатады.
Әдебиет:
- Қ.Жетпісов, Математикалық логика және дискретті математика.-Алматы:ЖШС РПБК «Дәуір»,2011ж.
- Зыков А. А. Основы теорий графов.М.:Наука,1987ж.
- Салғараева Г. И. Графтар теориясы:Алматы:ЖШС «Дәуір»,2013.







