Метод парных интегральных уравнений



Решение задач дифракции волн в упругом теле на различных включениях имеет существенное значение для ряда технических проблем. На нем, в частности, основаны методы неразрушающего контроля, позволяющие по характеристикам волнового поля делать заключения о наличии в теле дефектов [1]. Существуют различные математические методы решения задач дифракции.

Рассмотрим плоскую динамическую задачу теории упругости в области, представляющей собой плоскость с разрезом –a≤x≤a, y=0 (рис. 1).

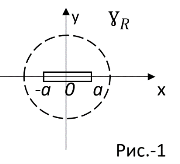
Этот разрез является математической идеализаций трещины, которая, как предполагается, имеет бесконечные размеры в направлении, перпендикулярном плоскости XY. Тело будем предполагать однородным и изотропным. Вектор смещения u=u(x,y,t) удовлетворяет системе уравнений Ляме

(λ+µ) grad div + µ ∆ = ρ , (1)

а также соответствующим начальным и граничным условиям. Граничные условия состоят в равенстве нулю напряжений

на краях трещины и условий на бесконечности. Вместо неизвестных функций удобно ввести потенциалы (x,y,t) и ψ(x,y,t), полагая

= grad + rot ψ ,

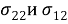
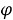
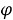
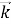
где k— орт оси, перпендикулярной k плоскости XY. В силу (1) они будут удовлетворять волновым уравнениям

∆ = 0,

,

∆ = 0, .

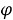
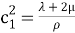
Здесь — скорости распространения волн расширения — сжатия и сдвига.

В дальнейшем мы будем рассматривать только установившиеся колебания тела с частотой ω, совпадающей с несущей частотой падающей монохроматической волны, которая вызывает эти движения. Тогда искомые потенциалы и могут быть представлены:

= Re , = Re ,

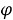
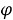
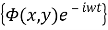
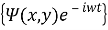
где , — комплекснозначные неизвестные функции. Они удовлетворяют уравнениям Гельмгольца

∆ + , ∆ +

.(2)

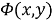
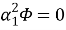
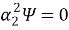
Здесь представляют собой волновые числа:

, .

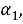
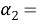
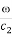
Падающую волну мы будем предполагать плоской и распространяющейся под углом θ к оси OX. Если эта волна является волной расширения — сжатия, то ее потенциалы могут быть представлены в виде

,

где i=1,2 и в случае падающей волны расширения — сжатия (j=1):

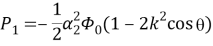
волны сдвига (j=1):

Следовательно

= Re ,

где . В случае падающей волны сдвига аналогично имеем

,

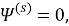
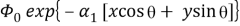
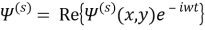
где

.

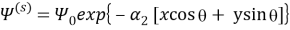
Функции ,

являются решением уравнением (2).

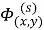
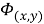
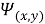
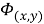
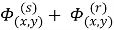
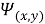
Представим искомые функции , в виде суммы:

= , = ,

где функции ,

– аналоги функций , для отраженных волн.

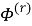
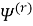
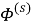
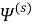
Введем некоторые комплексные функции , которые связаны с напряжениями соотношением:

= Re , (i,j = 1,2)

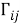
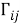
В нашем случае связаны с функциями

и :

, , .

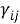
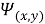
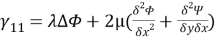
Пользуясь этими формулами, можно найти величины , соответствующие напряжениям, возникающим при распространения падающей волны. В случае волны расширения- сжатия:

;

;

.

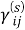
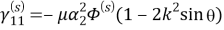
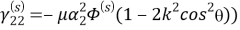
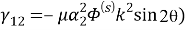
Для волны сдвига:

;

;

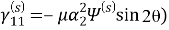
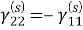
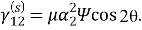
Равенство нулю нормального напряжения на краях трещины запишем в виде:

, .

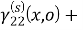
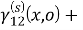
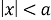
В итоге для неизвестных функций и получим краевую задачу:

;

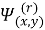
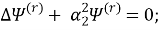
(x;y) ϵ \ ;

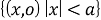
λ – = — ,

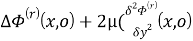
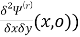
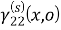
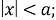
µ

= — ,

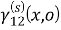
Кроме того должны выполняться условия излучения для ,

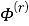
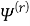
при что обеспечивают единственность решения краевой задачи.

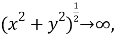
Литература:

1. Викторов И. А. Физические основы применения ультразвуковых волн Рэлея и Лэмба в технике. — М.: Наука, 1966г.
2. Ворович И. И., Бабашко В. А. Динамические смешанные задачи теории упругости для неклассических областей. — М.:Наука, 1979г.
3. Тихонов А. Н., Арсенин В. Я. Методы решения некорректных задач. — М.:Наук,1986г.