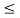Расходимость излучения передатчика космического аппарата



Современные космические системы зондирования Земли и околоземного космического пространства формируют большой объем информации о состоянии космического пространства, обработка которого в реальном масштабе времени на борту космических аппаратов (КА) затруднена и должна производиться с помощью наземных вычислительных средств. Но присутствуют ограничения на пропускную способность радиоканалов связи «борт — земля». Использование лазерной связи является одним из активно развиваемых направлений космической системы связи. Оптические каналы позволяют обеспечить большую пропускную способность при уменьшении габаритов антенных систем, снижения помех между каналами, а скорость передачи данных достигает 10 Гбит/с и выше. При этом бортовое оборудование связи характеризуется небольшими массогабаритными и энергетическими характеристиками. Важным элементом, обеспечивающим успешное решение задач функционирования космических систем зондирования Земли, являются высокоскоростные помехозащищенные линии связи, поэтому лазерные системы связи выступают важной составляющей перспективных средств дистанционного зондирования Земли и связи.

Беспроводная лазерная связь основывается на передаче данных модулированным излучением в инфракрасной части спектра. Данные в передатчике кодируются помехоустойчивыми кодами, модулируются лазерным излучателем, фокусируются оптической системой в узкий компилированный луч и передаются в направлении приемника [1].

В настоящий момент существует ряд факторов, ограничивающих применение лазеров для связи между космическими аппаратами и наземными станциями. Это расхождение лазерного луча, и сложность точного наведения на больших расстояниях. В связи с этим усложняется оборудование и принципы приема-передачи сигнала.

Оценим один из основных параметров лазерных систем — угла расходимости излучения.

Ошибки наведения оси излучателя энергии на приемник при некоторых упрощающих предположениях могут быть описаны законом распределения Релея.

Закон распределения Релея определяется по формуле (1):

, (1)

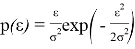
где — плотность распределения случайной величины

;

— угловая ошибка наведения;

– среднеквадратическое отклонение ошибок наведения.

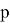
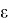
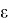
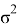
Вероятность появления ошибок, превосходящих некоторое заданное значение определяется по формуле (2):

, (2)

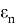
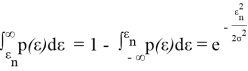
Если эту вероятность положить равной некоторой достаточно малой величине , то получаем уравнение (3):

(3)

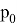
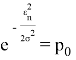
Уравнение (3) позволит определить значение ошибки, удовлетворяющей условию (4):

, (4)

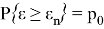
Найденную из (3) величину целесообразно рассматривать как «предельную» ошибку наведения и в проектных оценках параметров лазерных систем связи ориентироваться именно на это «гарантированное» значение точности наведения. Подобный подход позволяет получить простую формулу для оценки угла расходимости лазерного луча [3].

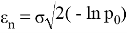
Обычно энергетическую освещенность в центре кружка приравнивают к единице, тогда форма луча в сечении в дальней зоне описывается функцией Эйри: , (5)

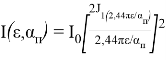
где  полная расходимость лазерного луча;

 длина волны;  функция Бесселя первого рода (рис. 1);  энергетическая освещенность на оси луча; — диаметр главного зеркала передатчика.

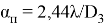
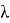
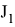
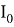
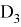
Интенсивность рисунка Эйри соответствует выражению (4), которое определяется функцией Бесселя 1-го рода.

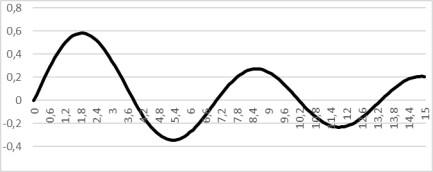
Рис. 1. Функция Бесселя 1-го рода

Нули J ₁ ( x ) находятся в точках, где x = 3.8317; 7,0156; 10,1735 и т. д. Из этого следует, что первое темное кольцо в дифракционной картине возникает там, где x = 3.8317.

Обозначим .

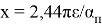
Тогда формула (5) примет вид:

, (5)

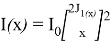
где — энергетическая освещенность на оси луча, ( ) =1;

— энергетическая освещенность на расстоянии от центра диска Эйри.

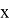
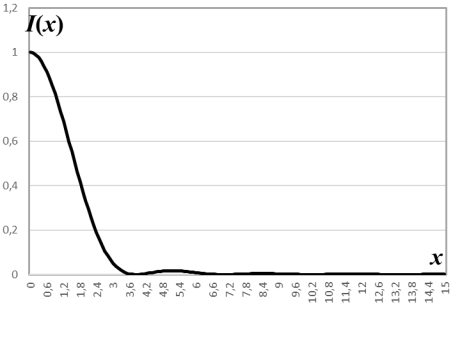
Рис. 2. Энергетическая освещенность 𝐼(𝑥) на расстоянии x от центра диска Эйри

Следовательно, мощность, принимаемая удаленным КА-приемником, будет определяться мощностью передатчика , потерями в оптических трактах, площадью приемника , расстоянием между передатчиком и приемником L , углом расходимости и поведением во времени ошибки

наведения . Пытаясь максимизировать принимаемую КА-приемником мощность, можно сделать это для самого неблагоприятного случая, когда ошибка наведения «предельная». Тогда выражение для (6) может быть записано в виде:

(6)

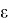
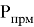
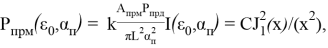
где k — коэффициент, учитывающий потери мощности в приемнике и передатчике;

С — константа, а

.

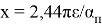
Принимаемая мощность прямо пропорционально зависит от .

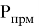
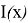
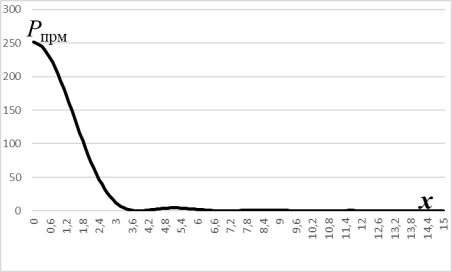
Рис. 3. Принимаемая мощность 𝑃прм на расстоянии x от центра диска Эйри

Из графика видно, что при освещенность в центре изображения максимальна. Найдем значение , определяющее размер кружка рассеяния мощности

. По мере удаления от центра освещенность быстро падает и достигает нулевого значения при (функция имеет минимум), следовательно, искомое значение может быть определено из условия

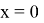
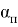
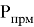
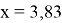
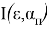
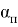
2,44

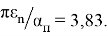
Подставляя сюда выражение для из (4), получаем уравнение (7):

, (7)

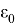
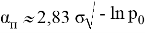
Пример:

Возьмем и . Угол расхождения в таком случае равен (рад). Предельная угловая ошибка будет равна . В таком случае . Что означает, что освещенность в этой точке будет равна 0. В расчетах мы использовали предельную угловую ошибку наведения, на практике же эта ошибка будет меньше предельной. Следовательно, и освещенность будет попадать в промежуток где будет максимум принимаемой энергии.

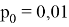
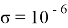
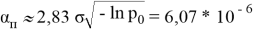
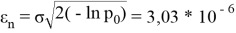
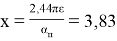
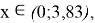
В таблице 1. показано, как меняется принимаемая мощность в зависимости от угловой ошибки наведения при оптимальном угле расходимости.

Таблица 1

№ п/п	ε ε п	x	P прм , Вт
1	3,03E-06	3,822546923	0,0009335
2	1,50E-06	1,892349962	94,37159547
3	9,00E-07	1,135409977	179,4719523
4	8,00E-07	1,009253313	192,7063144
5	5,00E-07	0,630783321	226,1391495

Возможность оптимизации величины расходимости в данном случае появилась из-за неоднозначного влияния угла расходимости на мощность (

) при конечном отличном от нуля значении. Действительно, если мало, то принимаемая мощность уменьшается в результате того, что направление на приемник часто оказывается вне конуса излучения; если велико, то принимаемая мощность также уменьшается, вследствие низкого уровня энергии в луче, обусловленного его шириной. Максимум принимаемой мощности будет между этими двумя значениями, а оптимальное значение определяется выражением (7).

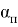
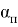
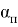
Литература:

1. Карцан, И. Н. Генетический алгоритм многокритериальной условной оптимизации бортового комплекса управления / И. Н. Карцан // Решетневские чтения. — 2016. — Т. 1. — С. 269–271. — EDN XEAEUD. — Текст: непосредственный.
2. Перунов, Ю. М. Зарубежные радиоэлектронные средства. В 4 кн. Кн. 2. Системы радиоэлектронной борьбы / Ю. М. Перунов, В. В. Мацукевич, А. А. Васильев // под. ред. Ю. М. Перунова. — Москва: Радиотехника, 2010. — 352 с. — ISBN 978–5–88070–272–5. — Текст: непосредственный.
3. Efremova, S. V. An ordered ranking multi-attributive model for decision-making systems with attributes of control systems software / S. V. Efremova, I. N. Kartsan, A. O. Zhukov // IOP Conference Series: Materials Science and Engineering, Krasnoyarsk, 20–21 ноября 2020 года / Krasnoyarsk Science and Technology City Hall. — Krasnoyarsk, Russian Federation: IOP Publishing Ltd, 2021. — P. 12068. — DOI 10.1088/1757–899X/1047/1/012068. — EDN SAXMGY. — Text (visual).