Бұл мақалада оптикалық диапазондағы жартылай өткізгіш нанобөлшектердегі оптикалық инверсия эффектісі теориялық зерттелді.
Кілтті сөздер: оптикалық инверсия, дисперсті орта, нанобөлшектер, көлемдік үлес.
В данной статье теоретически исследуются эффекты оптической инверсии в полупроводниковых наночастицах в оптическом диапазоне.
Ключевые слова : оптическая инверсия, дисперсная среда, наночастицы, обьемная доля.
Зерттеу нысаны ретінде титан диоксидінің тығыз орналастырылған полидисперсті сфералы нанобөлшектері алынған. Зерттеулер нәтижесі бойынша қабат қалыңдығы кішірейгенде қабаттағы бөлшектердің көлемдік үлесі артады, ал ол өз кезегінде екі зерттелетін жүйенің өткізгіштік қасиетіне әсер етеді. Өлшемдері 25 нм төмен бөлшектердің қабатының өткізгіштік қабілеті төмендейді, ал өлшемдері 100 нм бөлшектер қабатының өткізгіштік қабаты артатыны белгілі болды. Бұл ерекшеліктің интерпретациясы «тікелей» және «инверсті» шашыратқыш жүйелер туралы ұғымды қолдану арқылы берілуі мүмкін. 1 суретте үлгілердің диффузиялық өткізу спектрлерінің қысылуға дейінгі (1,3) және (2,4) кейінгі мысалдары көрсетілген. Барлық спектрлер үшін қзын толқынды облыстарда
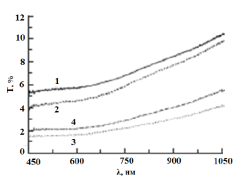
Сурет 1. Титан диоксидінің тығыз орналасқан бөлшектерінің диффузиялық өткізу спектрлері: 1 — қабатының қалыңдығы
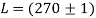
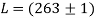
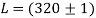
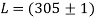
Алынған мәліметтерді интерпретациялау үшін жүйедегі шашыратқыш орталықтардың
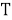
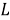
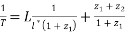
бұл жердегі
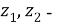
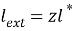
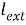
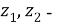
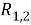
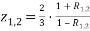
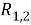
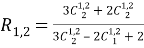
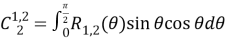
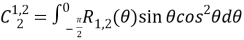
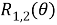
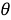
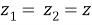
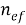
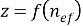
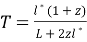
Айта кететін жағдай,
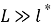
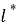
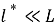
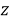
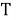
Кешенді сыну көрсеткіші бар кеңістікті біртекті ортаның тиімді модельдерінің әртүрлі нұсқасын Буш және Соукоулис өз еңбектерінде қарастырды [1]. Біздің жағдайда шашыратқыш орталардың тығыз орналасуының
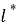
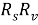
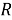
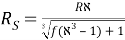
бұл жердегі א–шамамен 1,65 тең болатын келтіру параметрі.
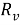
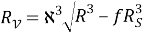
Жалпы жағдайда оптикалық тасымалдау параметрлерін табу үшін қолданылатын итеративті процедура минимумға келтіріледі. Бұл процедура мына теңдікпен өрнектелген:
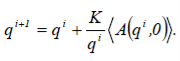
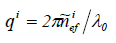
Абсолют шаманың минимал мәніне жеткенде процедура тоқтайды, ал модельденетін ортаның шашырау ұзындығының шамасы мен сыну көрсеткішінің тиімділік шамасын анықтап аламыз. Осылайша, тиімді ортаның табылған сыну көрсеткішінің нақты бөлігі нақты ортаның
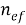
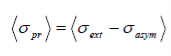
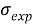
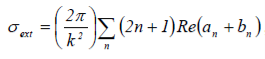
асимметрия қимасының шамасы:
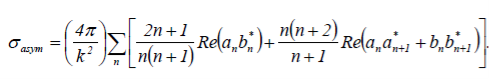
бұл жердегі
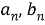
Жоғарыда көрсетілген модель субмикронды және наноөлшемдегі бөлшектерден тұратын дисперсті наножүйелердің оптикалық тасымалдау параметрлерін есептеуге мүмкіндік береді [3].
Әдебиет:
- Громаков Н. С. Дисперсные системы и их свойства. — Казань: Изд-во Казанск. гос. архитект.-строит. ун-та, 2015. — 91 с.
- Беляев А. П. Физическая и коллоидная химия / Беляев А. П., Кучук В. И., Евстратова К. И. и др. /Под ред. А. П. Беляева. — Москва: ГЭОТАР-Медиа, 2010. — 704 с.
- Кругляков П. М., Хаскова Т. Н. Физическая и коллоидная химия. — М., 2005. — 320 с.







