В статье описывается теория и методика обучения математике. Для более эффективного освоения курса геометрии учениками была представлена методика обучения математическими моделями. В данной работе представлена классификация моделей объектов и требования к моделям. Показана взаимосвязь между наглядными пособиями и моделями объектов. Приводится подробный план использования моделей в классе в соответствии с классификацией. Также представлены методические аспекты создания моделей. Для наглядной работы моделей был приведен пример, который призван помочь педагогам эффективно применять данную методику обучения. Основной целью данного исследования было изучение теоретических аспектов и разработка практических рекомендаций по применению данной модели на уроках планиметрии в средних школах. Для эффективного обучения и освоения всех разделов геометрии можно применять наглядные модели. Для достижения результатов исследования проводился анализ работ известных математиков, таких как Я. А. Коменский, К. Д. Ушинский и др.
Ключевые слова: математика, геометрия, планиметрия, стереометрия, модель.
Введение. Одной из самых важных тем в математике является геометрия. В процессе обучения учащиеся должны приобрести глубокие и прочные знания по этому предмету и умение осмысленно применять их на практике. Однако опыт учителей математики показывает, что качество знаний и умений по геометрии у учащихся с базовыми академическими способностями невысокое. Это объясняется тем, что геометрия является относительно сложным предметом по сравнению с другими предметами математического цикла и на ее изучение традиционно отводится меньше времени. Поэтому в данном контексте возникает проблема, как дать учащимся знания более высокого порядка. Одним из решений этой проблемы является эффективное использование объектных моделей на уроках планиметрии. Однако согласно наблюдениям за работой учителей математики и анализу литературы и журналов по математической методике, использование объектных моделей на уроках геометрии является недостаточным и в основном используется для демонстрации пространственных моделей объектов на уроках стереоскопического зрения. Способность мысленно представлять положение объектов в пространстве должна была быть развита задолго до периода обучения стереометрии. Однако при изучении планиметрии использованию моделей уделяется меньше внимания [1].
Это может быть связано с недостаточно развитым использованием объективной модели и с тем, что, хотя объективная модель может значительно улучшить обучение и помочь повысить и поддержать интерес к предмету, ее потенциал часто недооценивается учителями математики. Основной целью данного исследования было изучение теоретических аспектов и разработка практических рекомендаций по применению данной модели на уроках планиметрии в средних школах. Для эффективного обучения и освоения всех разделов геометрии можно применять наглядные модели.
Что касается роли визуализации в математике, то великий математик Д. Гильберт сказал: «В математике существуют две тенденции. Тенденция к абстракции заключается в развитии логического представления на основе различных материалов и приведении этих материалов в систематическую взаимосвязь; другая тенденция — это визуализация».
Визуализация используется для приобретения знаний о внешних свойствах математических объектов, отношениях между объектами и их сходствах и различиях. Роль визуализации заключается в том, чтобы предоставить учащимся возможность показать глубинные взаимосвязи между свойствами математических объектов. Психологи считают, что для правильного подбора и использования визуализаций в классе важно определить поведение учащихся по отношению к средствам визуализации и действия, которые им необходимо предпринять для сознательного усвоения материала [2].
Методы. Для написания данной работы проводился анализ работ известных математиков как: Я. А. Коменский, К. Д. Ушинский, а также психолог А. Н. Леонтьев и др.
Результаты. Изучение формы геометрических тел, обучение рисованию, анализу, рассуждениям и доказательствам на плоскости, столе или бумаге и развитие пространственного мышления являются основными задачами преподавания математики в школах. Для развития пространственного мышления и его представления используются наглядные пособия, такие как предметы окружающей среды, технические устройства и созданные модели.
Особую роль в развитии пространственного представления играет планиметрия. Это связано с тем, что планетарные образы легко представить. Работа с моделями не только помогает учащимся представить себе формы, но и развивает пространственное мышление. После работы с моделями учащиеся будут более способны составлять композиции и конструировать на плоских поверхностях. Методолог В. В. Давыдов понимает «модель» как образ (в том числе условный или мысленный) или прообраз (образец) объекта или системы объектов («прототип» этой модели), который при определенных условиях будет использоваться как «заменитель» или «представитель». Под моделью понимается представление фактов, вещей и отношений в определенной области знаний в виде простой и более легко различимой материальной структуры [3]. Используемые модели для изучения курса геометрии можно увидеть на рисунке 1.
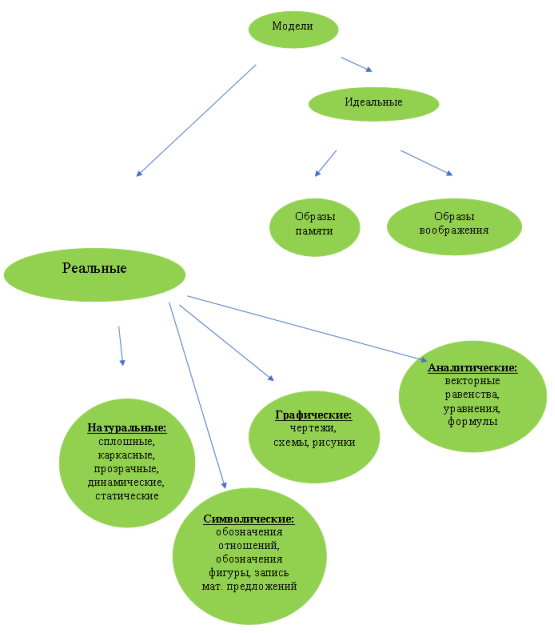
Рис. 1. Геометрические модели преподавания
Данные модели возможно применять в абсолютно всех этапах процесса преподавания. Стадия осознания познаний, стадия пояснения новейшего использованного материала педагогом, стадия закрепления выученного материала, стадия развития навыков, а также умений, стадия выполнения домашнего задания, стадия контролирования освоения выученного материала. Разберем применение наглядных пособий при освоении планиметрии на главных стадиях преподавания: осмысление знаний, исследование новейшего материала, фиксирование выученного материала, а также контроль усвоения выученного материала.
Практическое применение этапа знаний направлено на усвоение учащимися текущего материала, использование имеющихся знаний в типичных и актуальных ситуациях, приобретение определенных навыков, стимулирование познавательной деятельности учащихся и контроль преподавателем уровня усвоения знаний. Для достижения этих целей в начале выполнения задания проводятся стереометрическая, кинематическая и планетарная модификации. В непосредственном действии необходимо выяснить связь между ранее изученным, а также между неизвестным и общим материалом. Это помогает систематизировать используемый материал, углубить понимание и выработать прочные знания [4].
На этапе актуализации знаний более целесообразно применять последующие модификации.
При исследовании темы «Взаимное расположение двух окружностей» возможно применять модели двух окружностей.
С целью данного исследования, пред учениками устанавливается задача: «Как могут находится две окружности относительно друг друга?» В руках педагога две модели. Один из обучающихся свидетельствует то, что окружности имеют все шансы пересекаться. Преподаватель четко демонстрирует им данное на моделях, а также задает последующий вопрос (тут же преподаватель анализирует случай, если окружности совпадают): какое количество общих точек имеют окружности?
Следующий случай, когда окружности не пересекаются. Учитель снова задает тот же вопрос. Затем делаются выводы о том, как должны располагаться окружности. Затем учащиеся приступают к изучению нового материала.
Этап изучения нового материала. Это важный этап в структуре урока. На этом этапе или в связи с ним в курсе рассматриваются вопросы закрепления нового материала и управления усвоением ранее изученного материала.
Цель курса на этом этапе — освоение учащимися нового материала. Новый материал объясняется самим учителем, в процессе работы с учениками или отрабатывается самими учениками. При изучении нового материала решаются вопросы, связанные с усвоением, такие как понимание, запоминание и применение. При изучении нового материала также важно обеспечить «знакомство» учащихся с материалом. Этого можно достичь, определив ключевое содержание, которое необходимо усвоить. Справочные термины должны быть представлены таким образом, чтобы учащиеся могли использовать их правильно с первого раза. Этого можно достичь с помощью кратких конспектов, подходящих примеров применения нового материала для решения задач и т. д. [5].
Заключение. Таким образом, применяя перечисленные выше модели можно применять для эффективного обучения планиметрии. В процессе изучения новых планиметрических материалов можно использовать модели, сделанные из сложенной бумаги. Например, сложив лист бумаги, можно получить изображение отрезка. Если сложить дважды правильным образом, то можно получить изображения углов, смежных углов, перпендикулярных углов, параллельных прямых и т. д. Складные модели (треугольник, трапеция и т. д.) также можно использовать для мотивации решения той или иной задачи.
Литература:
- Болтянский В. Г. Формула наглядности — изоморфизм плюс простота / В. Г. Болтянский // Педагогика. — 2015. — № 15. — с. 46–60;
- Бурмистрова Н. В. Наглядная геометрия: учебник для учащихся 9-го класса / Н. В. Бурмистрова, Н. Г. Старостенкова. — Саратов, 2021. — 48 с;
- Волович М. Б. Наука обучать, Технология преподавания математики / М. Б. Волович. — М. LINKA-PRESS, 2017. — 280 с;
- Геометрия: учеб. для 7–9 кл. сред. шк. / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев [и др.]. — М. Просвещение, 2018. — 335 с;
- Дорф П. Я., Наглядные пособия по математике. — М.2020, 160 с.







