Ключевые слова: многочлен, остаток, следствие, целый коэффициент, необходимое и достаточное условие, найти корень, наибольший общий делитель (НОД), алгоритм Евклида, делитель целого числа.
Keywords: polynom, residual, conslusion, integer,necessary and enough, search a root, greatest common divisor or highest common factor(GCD or HCF), factor of an integer, degree.
При изучении математики многочлены играют важную роль, а также в теореме Вейерштрасса, которая является одной из основных теорем математического анализа. Теорема Безу посвящена многочленам.
Пусть
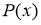
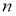
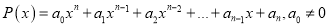
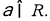
Теорема Безу.
Остаток от деления многочлена
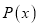
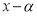
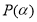
Доказательство:
Необходимость.
Если многочлен
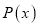
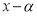
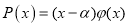
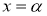
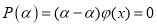
Достаточность.
Пусть
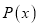
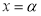
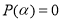
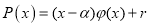
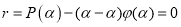
Следствия теоремы Безу (деление двучлена
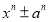
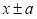
-
Разность одинаковых степеней двух чисел делится на разность этих чисел без остатка. Потому, что по теореме Безу остаток от деления двучлена
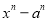
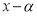
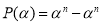
-
Сумма одинаковых степеней двух чисел не делится на разность этих чисел без остатка. Потому, что по теореме Безу остаток от деления двучлена
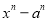
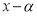
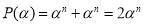
-
Разность одинаковых четных степеней двух чисел делится на сумму этих чисел без остатка, а нечетных степеней не делится. Потому, что по теореме Безу остаток от деления двучлена
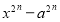
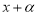
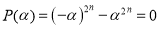
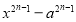
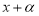
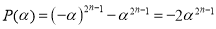
-
Сумма одинаковых нечетных степеней двух чисел делится на сумму этих чисел без остатка, а четных степеней не делится. Потому, что по теореме Безу остаток от деления двучлена
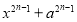
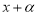
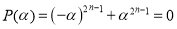
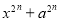
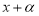
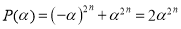
Следствие 1.
Если многочлен
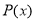
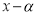

В общем случае верно и обратное.
Следствие 2.
Если
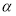
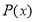
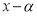
Таким образом, эти два условия являются необходимыми и достаточными условиями друг для друга.
Следствие 3.
Если
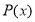
Следствие 4.
Остаток от деления многочлена
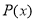
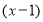
Некоторые применения теоремы Безу:
1. Нахождение корней многочлена

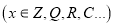
Обычно, если отношение свободного члена
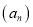
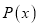
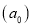
1. Сначала найдем целые делители главного коэффициента
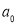
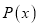
2. Числа, которые могут иметь рациональные корни:
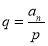
3. Проверяются всевозможные числа, т. е. должно выполняться условие
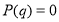
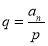
Пример 1.
Найдите корни многочлена
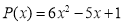
Решение.
Вданном примере главный коэффициент отличен от 1. Поэтому сначала проверяем:
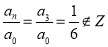
1. Найдем целые делители главного коэффициента
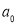
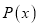
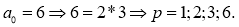
2.
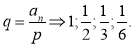
3.
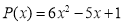
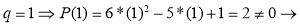
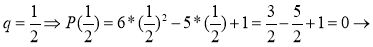
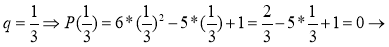
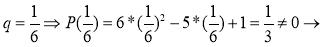
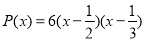
Ответ:
Данный многочлен
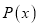
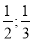
2
. Напомним, что остаток от деления многочлена
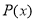
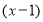
Сумму коэффициентов
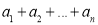
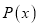
Пример 2.
Найти сумму коэффициентов многочлена
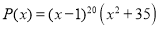
Решение.
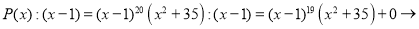
Данный многочлен делится на
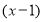
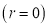
3. Нахождение корней многочлена
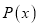
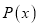
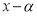
4.
Теорема Безу может быть применена к определению, является ли число
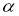
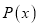
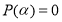
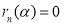
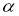
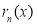
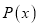
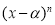
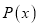
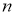
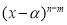
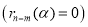
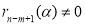
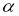
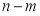
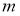
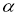
5. Применяется для выполнения алгоритм Евклида. При этом, если заданы два многочлена
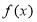
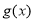
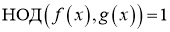
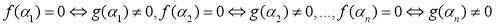
6. Теорема Безу использовалась для решения как стандартных, так и некоторых нестандартных задач.
Пример 3.
Доказать, что число
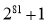
Решение. Вследствии теоремы Безу мы показали, что сумма одинаковых нечетных степеней двух чисел делится на сумму этих чисел без остатка.
Отсюда следует, что двучлен
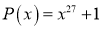
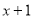
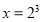
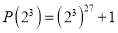
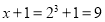
Следовательно,
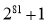
Пример 4.
При каком значении параметра
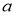
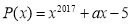
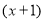
Решение.
По теореме Безу для того, чтобы многочлен
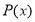
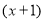
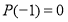
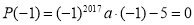
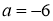
Ответ:

Пример 5.
При каком значении параметра
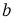
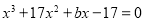
Решение.
Если ввести обозначение
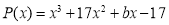
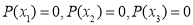
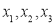
Для данной задачи решения должны быть целые числа. Поэтому мы находим целые делители свободного члена данного многочлена и проверяем используя теорему Безу.
Здесь свободный член
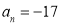
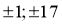
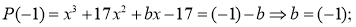
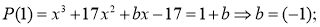
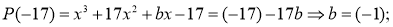
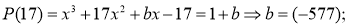
Здесь число 17 не является корнем. Потому, что значение параметра
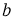
Замечание.
Уравнение не имело бы трех целочисленных решений, если бы количество значений, отличных друг от друга, было больше единицы, когда проверили возможные целые значения
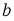
В нашем случае значения параметра
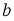
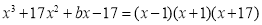
Уравнение имеет целые
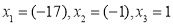
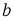
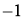
Ответ:
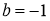
Пример 6:
При каком значении
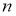
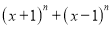
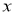
Решение. Согласно теореме Безу, чтобы многочлен
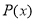
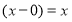
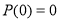
Если многочлен
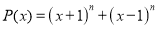
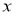
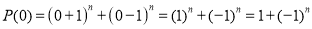
Следовательно,
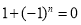
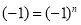
Ответ: n — произвольное нечетное натуральное число.
Пример 7.
Найти остаток отделения многочлена
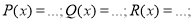
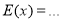
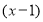
Решение.
Согласно теореме Безу этот остаток равен значению заданного многочлена при
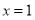
Ответ:
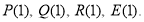
Пример 8.
Остаток от деления многочлена
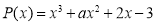
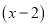
Остаток от деления многочлена
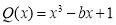
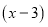
Остаток от деления многочлена
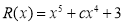
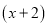
Найти остаток от деления многочлена
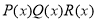
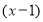
Решение.
Используя теорему Безу, запишем параметры
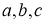
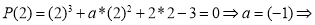
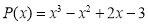
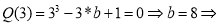
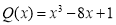
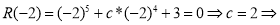
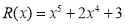
Согласно теореме Безу остаток от деления многочлена
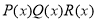
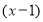
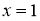
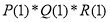
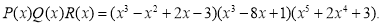
Следовательно,
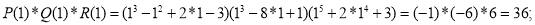
Ответ: 36.
Пример 9.
Делится ли многочлен
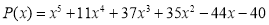
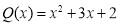
Решение. Согласно теореме Безу, если корни многочлена
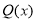
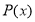
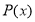
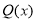
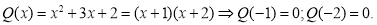
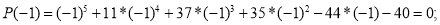
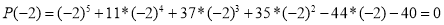
Ответ: Многочлен
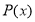
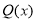
Пример 10.
Существует ли многочлен
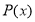
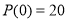
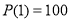
Решение.
Согласно теореме Безу остаток от деления многочлена
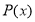
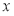
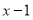
Пусть
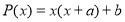
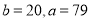
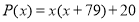
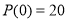
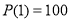
Ответ:
Да, существует. Например
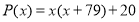
Литература:
- Винберг Э. Б. Курс алгебры, — М.: Издательство «Факториал Пресс», 2002, ISBN 5–88688–060–7.
- Piotr Rudnicki (2004). «Little Bézout Theorem (Factor Theorem)" Formalized Mathematics. 12 (1): 49–58.
- Andrzej Trybulec. On the sets inhabited by numbers. Formalized Mathematics, 11(4):341–347, 2003.







