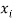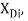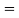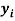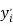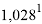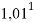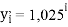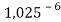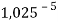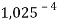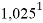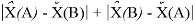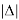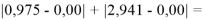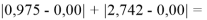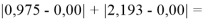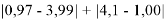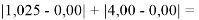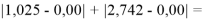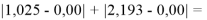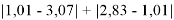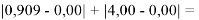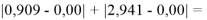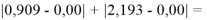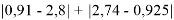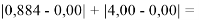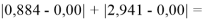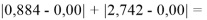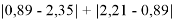Алгоритм расчета электроотрицательностей атомов в таблице Д. И. Менделеева на основе энергий диссоциации



Настоящее исследование посвящено разработке алгоритма для расчета электроотрицательности (ЭО) атомов. Основное внимание автора было сосредоточено на изучении табличных данных и применении различных методов для их обработки с целью расчета ЭО атомов с повышенной точностью. Актуальность исследования заключается в том, что экспериментальные последовательности ЭО еще недостаточно изучены. Определяющим фактором использования в вычислениях значений энергии диссоциации простых молекул явилась возможность рассчитать более точные значения ЭО за счет отсутствия в самих вычислениях неточных значений радиусов атомов . Цель исследования — это определение максимально точных значений ЭО в первой и седьмой группах таблицы Д. И. Менделеева; выявление физической природы самого понятия ЭО; раскрытие свойств энергии диссоциации простых молекул. В качестве гипотезы исследования было принято положение о том, что максимальное значение ЭО химического элемента, находящегося в первой группе таблицы Д. И. Менделеева, близко к единице и принадлежит интервалу 1,023–1,032. Теоретическая значимость настоящей работы заключается в том, что сформулированные положения позволят отказаться от ряда постулатов и дать предложения по дальнейшему использованию таблиц энергий диссоциации.

Ключевые слова : электроотрицательность (ЭО), шкала Оллреда-Рохова, регрессионный анализ, метод последовательных приближений, метод наименьших квадратов, энергия диссоциации.

1. Особенности методов расчета электроотрицательности атомов

1.1 Об учении электроотрицательности атомов

Учение об электроотрицательности (ЭО) является одним из давних разделов общей химии, основу которому положил Берцелиус. Изначально учение носило только качественный характер. Первая количественная шкала ЭО была разработана Лайнусом Полингом в 1932 году. При этом, под ЭО понималась способность атомов притягивать к себе чужие электроны [1;2]. В настоящее время существует более двадцати шкал ЭО, в основу которых положены различные свойства веществ и элементов. Однако само понятие ЭО и методы ее определения еще не имеют общего понимания среди научного мира. Это обстоятельство не позволяет однозначно объяснить как физическую сущность ЭО, так и ее роль в происходящих химических процессах. Тем не менее, понятием ЭО широко пользуются в общей химии. Оно может быть выражено в численном виде и отнесено к какой-либо определенной шкале [3]. Необходимо отметить что, одни шкалы ЭО имеют размерность физических величин, а другие нет [2].

Полинг постулировал ЭО значение фтора F = 4,0; H = 2,1, также им было принято значение ЭО элементов от углерода до фтора в диапазоне от 2,5 до 4,0 [1]. Сам Полинг характеризовал точность рассчитанных им значений ЭО атомов как очень низкую (до одного знака после запятой) [4].

Определенную часть ЭО атомов Полинг вычислил самостоятельно [4]. Рассчитать оставшиеся ЭО ему помог другой выдающийся ученый Альберт Л. Оллред [5]. Однако, в своей работе Оллред не только обновил исходные данные Полинга, но и использовал термодинамические данные для расчета значений ЭО атомов. Именно эти «пересмотренные значения» ЭО Полинга используются в научной литературе [1; 5].

Предложенное Полингом выражение для расчета разности в ЭО между химическими элементами A и B имеет вид:

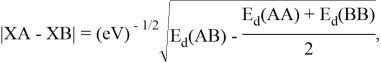
в котором энергии диссоциации

связей A — B, A — A и B — B имеют размерность в эВ. Для выбора произвольной точки отсчета производилось взаимное согласование ЭО с использованием большого числа термохимических данных по энергиям связи. Оно осуществлялось таким образом, чтобы наиболее электроотрицательным элементам от C до F приписать значения от 2.5 до 4.0 [3]. Энергия связи и энергия диссоциации связи — это эквивалент величин энергий химической связи между атомами. По существу энергия диссоциации это именно та энергия, которая необходима для разложения молекулы на атомы [2].

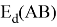
Известно [2], что два атома образуют химическую связь за счет своих электронов. В одном случае какой-либо из двух атомов отдает валентные электроны другому и образуется ионная связь. В другом — оба атома в равной мере вкладывают свои валентные электроны. При этом формируется общая группа электронов, образующая ковалентную связь. Чисто ковалентные связи в химии — это исключительные случаи. Чаще встречаются ситуации, когда образуются ковалентные полярные и ионные связи. Именно это обстоятельство и учитывал Полинг при создании своей шкалы ЭО.

Сравнивая энергию связи c полусуммой энергий чисто ковалентных связей E(A и , Полинг пришел к выводу, что разница энергий E(A ] по своей сути является проявлением полярного характера связи атомов A и B [2]. Он также определил, что можно разложить на термы, соответствующие атомам A и B ( ), а пересчитав размерность из килокалорий в электрон-вольты получить еще и формулу для расчета ЭО:

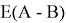
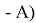
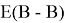
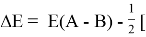
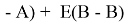
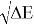
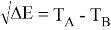
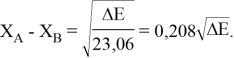
Из данной формулы следует, что энергия диссоциации двухатомных молекул содержит достаточно необходимой информации о ЭО атома. Поэтому она представима в виде алгебраической функции от ЭО атомов: . Преимуществом энергии диссоциации является возможность вычислять ЭО химических элементов в эВ без использования значений их атомных радиусов.

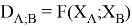
Известный российский ученый Артем Оганов скептически относится к расчетам ЭО на основе энергии диссоциации (энергии связи). Он считает: «что из энергий связей невозможно получить электроотрицательности, приведенные в каждом учебнике. Мы обратились к экспериментальным данным и тоже не нашли совпадений. Вообще непонятно, откуда взялась таблица значений электроотрицательности. Это загадка. Если порыться в литературе, то оказывается, что этот эффект был известен. Но мы были потрясены тем, что он упоминается вскользь, шепотом, у него даже есть смешные называния, например «размерный эффект» [6; 7; 8].

Таким образом, работа Полинга «ЭО как функция от энергии диссоциации» превратилась в гипотезу.

Одна из наиболее известных и востребованных шкал ЭО, основанная на эффективном заряде ядра атома и ковалентном радиусе атома, принадлежит Альберту Л. Оллреду и Юджину Г. Рохову. Считается, что в данном случае ЭО определяется как кулоновская сила притяжения электрона к одному из двух ядер:

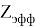
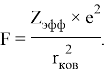
Найденное ими эмпирическое соотношение [9] дало хорошие совпадения величин ЭО со шкалой Полинга:

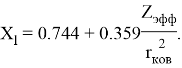
В 2022 году на основе энергии ионизации была создана новая шкала ЭО. Рассчитанные по этой шкале значения ЭО отличаются не более чем на от значений ЭО шкалы Оллреда и Рохова. Особенностью новой шкалы является тот факт, что она действует только в пределах какого-либо одного периода таблицы Д. И. Менделеева и использует в качестве основных орбитальные радиусы [10].

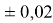
Опорными ЭО для данной шкалы являются: ЭО углерода C, кремния Si, германия Ge, олова Sn и свинца Pb. Однако, в качестве опорных элементов ЭО могут быть выбраны и другие вещества. Например: литий Li, натрий Na, калий K, рубидий Rb, цезий Cs. Расчет ЭО химических элементов осуществлялся по выражению:

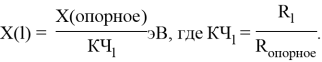
1.2. Выбор математического аппарата для обработки эмпирических данных и установления зависимостей

Применение метода регрессионного анализа (или иначе метода наименьших квадратов) для обработки изучаемых эмпирических последовательностей известно давно. Наилучшей полученной аналитической зависимостью считается та, которая изначально основывается на особенностях изучаемого процесса. Самой главной особенностью регрессионного метода является его способность учитывать взаимосвязь экспериментальных значений и тем самым осуществлять их сглаживание или «исправление» (выявлять зависимость) [11; 12].

Используемый в работе математический аппарат подбора аппроксимирующих функций и расчет их точности заимствованы из [11].

Применялся также метод последовательных приближений и другие аналитические методы.

2. Особенности расчета электроотрицательности на основе энергии диссоциации

2.1. Алгоритм расчета ЭО атомов первой группы таблицы Д. И. Менделеева

Известный российский ученый профессор Сколтеха Артем Оганов, давая интервью журналисту РИА Новости [7], высказал свое отношение к шкале ЭО Полинга. «Мы использовали определение Полинга для расчета электроотрицательности в нормальных условиях и были поражены, обнаружив, что ее масштаб не соответствует ни теоретическим, ни экспериментальным энергиям связи. Более того, многие публикации в химической литературе упоминают об этом несоответствии, но ни одна не предлагает последовательного решения».

Тем не менее, в наших исследованиях использовались разности молекулярных энергий диссоциации. Так, например, при определении разности ЭО атомов X(Na) и X(K) была использована разность энергии диссоциаций молекул D(HNa) и D(HK) [13].

эВ

эВ

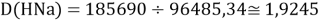
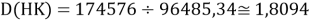
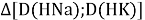
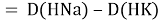
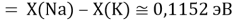
При определении ЭО X(K), X(Rb) и X(Cs) использовали разности:

эВ

эВ

0205 эВ

эВ;

эВ

эВ

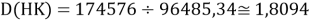
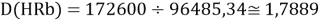
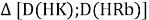
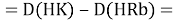
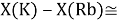
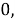
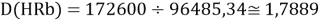
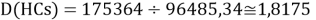
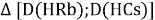
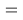
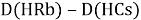
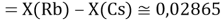
Сначала предположили, что значение ЭО X(Na) 1,01 [15] (метод последовательных приближений) . Тогда, так как

, то:

1,01 0,8948 эВ.

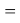
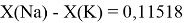
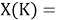
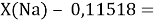
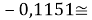
При X(Na) 1,02 эВ

1,02

0,9048 эВ.

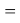
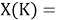
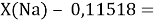
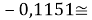
При X(Na) 1,03 эВ

1,03 0,9148 эВ.

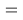
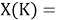
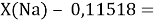
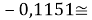
При X(Na) 1,025 эВ

1,025

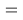
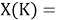
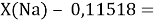
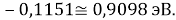
Из четырех рассчитанных значений наиболее близкое к рассчитанному в [14] является четвертое. Именно от него были рассмотрены остальные ЭО соответствующие для них разности:

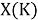
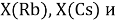
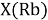
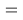
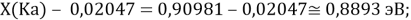
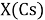
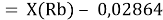
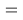
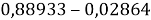
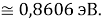
Сопоставляя полученные данные с данными из таблицы Оллреда и Рохова [15] отметили, что они практически совпадают кроме ЭО для , которое увеличилось на 0,015.

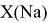
Иным подтверждением правильности расчета ЭО первой группы атомов стали вычисления их ЭО на основе других энергий диссоциаций молекул: D(NaNa), D(NaK), D(NaRb), и D(NaCs).

D(NaNa)

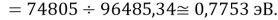
D(NaK)

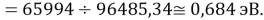
D(NaRb)

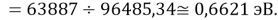
D(NaCs)

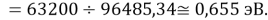
Нашли их соотношения и получили:

X(K) D(NaK) D(NaNa)

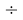
X(Rb) D(NaRb)

D(NaNa)

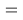
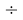
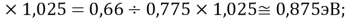
X(Cs) D(NaCs) D(NaNa)

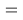
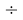
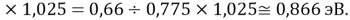
Данные результаты расчетов отличаются от представленных выше не более чем на 0,01.

При сравнении с табличными данными Оллреда и Рохова [15] суммарная погрешность аппроксимации при X(Na) равна:

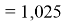
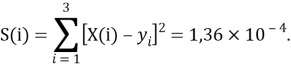
Предварительно вычисленные и обработанные значения ЭО атомов из первой группы таблицы Д. И. Менделеева приведены в таблице 1.

Таблица 1

Расчет значений аппроксимирующей функции для первой группы таблицы Д. И. Менделеева

Элемент	Cs	Rb	K	-	-	Li	Na
Номер	1	2	3	4	5	6	7
	0,8607	0,8893	0,9098	-	-	-	1,025
Y ln	0,1501	0,1173	0,0945	-	-	-
Рассчитанная ЭО	0,8620	0,8863	0,9113	-	-	-

Расчет значений аппроксимирующей функции для первой группы осуществляли с использованием метода наименьших квадратов [11;12] :

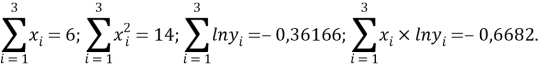
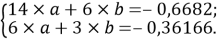
a

.

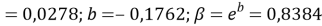
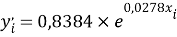
где знаменатель прогрессии равен:

q ,

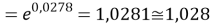
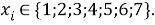
Суммарная погрешность аппроксимации при данном значении ЭО X(Na) равна

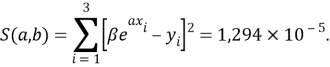
Сравнение приведенных выше результатов расчетов погрешностей показало, что значение ЭО лежит около

. Вместе с тем, расчет по методу наименьших квадратов с использованием показательной аппроксимирующей функции позволил считать, что значения ЭО атомов в первой группе расположены в порядке возрастающей геометрической прогрессии со значением знаменателя около 1,025. Действительно:

; ;

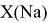
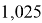
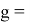
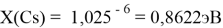
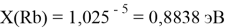
X(K) ;

; ;

;

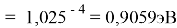
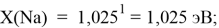
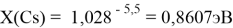
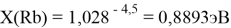
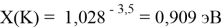
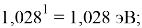
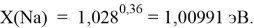
Однако последовательность со знаменателем 1,025 оказалась предпочтительнее тем, что целому значению показателя степени соответствует вполне определенный период. И, наконец, так как значение ЭО каждого химического элемента равно значению соответствующего члена геометрической прогрессии, то их можно представить в виде выражений:

и для X(K) и X(Rb), где X значение ЭО X(Na).

и

для X(Rb) и X(Cs), где X значение ЭО X(Na).

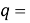
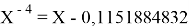
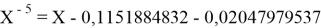
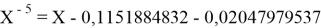
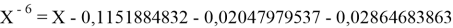
Решив ( аналитически ) отдельно две пары уравнений определили области значений ЭО X(Na).

, 1 ,

,

,

и

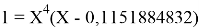
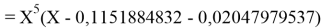
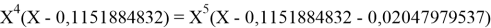
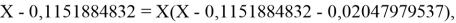
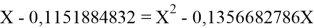
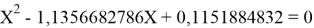
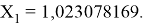
Вторая пара уравнений решается аналогично.

и 1

и

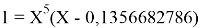
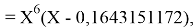
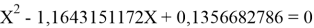
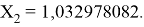
q ,

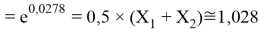
Решения данных уравнений достаточно достоверно определяют вариабельность значения ЭО X(Na), и тем самым подтверждают правильность выдвинутой нами гипотезы о том, что значение величины ЭО X(Na) практически близко к единице.

В таблице № 2 представлено сопоставление значений ЭО, рассчитанных из энергий диссоциаций, по методу наименьших квадратов и заимствованных из таблицы Оллреда и Рохова.

Таблица 2

Расчет значений аппроксимирующей функции для первой группы таблицы Д. И. Менделеева

Элемент	Cs	Rb	K	-	-	Li	Na
Номер	1	2	3	4	5	6	7
расчет из энергий диссоциаций	0,8600	0,8900	0,9100	-	-	0,97
ЭО Табличные данные	0,8622	0,8838	0,9059	-	-	0,97
Расчет ЭО						0,975

Точность расчетов сопоставлялась с помощью приведенных ниже выражений:

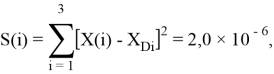
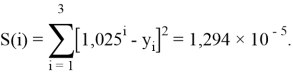
Пользуясь данными приведенных расчетов, определили ЭО атомов в первой группе таблицы Д. И. Менделеева:

X(Li ) X(Na) ; X(K) ; X(Rb) ;

X(Cs) .

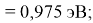
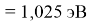
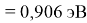
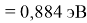
(Li) (Na) ; (K) ; (Rb) ; (Cs) .

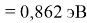
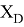
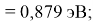
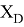
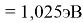
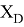
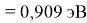
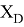
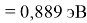
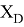
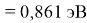
Данные расчеты отличаются от представленных выше не более чем на 0,01 (кроме Li).

При сравнении с табличными данными Оллреда и Рохова [15] суммарная погрешность аппроксимации при X(Na) равна

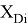
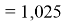
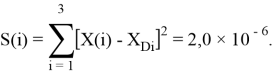
2.2 Алгоритм расчета ЭО атомов в седьмой группе таблицы Д. И. Менделеева

При расчете ЭО атомов в седьмой группе использовались энергии диссоциации следующих простых молекул: D(FF); D(FCl); D(FBr); D(FI). Здесь:

D(FF) 158670 96485,34

1,6445эВ;

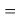
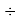
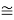
D(FCl) 260830 96485,34 2,7033 эВ;

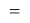
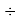
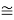
D(FBr) 280000 96485,34 2,902 эВ;

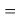
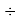
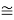
D(FI) 271500

96485,34 2,8139 эВ (надо полагать, что эти данные без учета энергии разрушения решетки). С учетом разрушения решетки

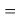
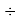
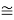
D(FI) 333500 96485,34 3,4513 эВ.

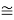
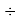
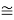
Для проведения дальнейших вычислений приняли гипотезу о том, что ЭО X(F) Тогда:

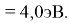
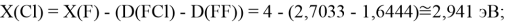
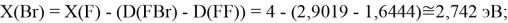
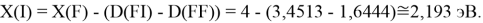
(Вычисленное значение для X(I) сомнительное). В данных расчетах использовались разности между энергиями диссоциаций соответствующих молекул [13].

Использовали и иной способ определения ЭО в седьмой группе — это отношения энергий диссоциаций.

D(HF) 569658 96485,34 5,9041 эВ;

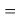
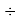
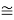
D(HCl) 431361

96485,34 4,4707 эВ;

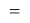
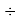
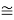
D(HBr) 366160 96485,34 3,7949 эВ;

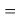
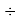
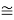
D(HI) 298260 96485,34 3,0912 эВ.

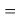
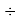
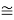
X(Cl)

X(F) D(HCl) D(HF) 4 5,90408 3,0289 эВ;

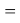
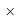
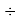
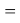
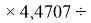
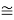
X(Br) X(F) D(HBr) D(HF) 4

5,90408 2,571 эВ;

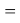
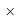
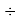
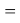
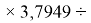
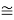
X(I) X(F) D(HI) D(HF) 4 5,90408 2,0943 эВ.

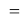
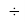
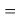
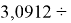
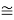
Для оценки достоверности вычислений ЭО атомов на основе энергий диссоциаций были проведены вычисления и с использованием энтальпий

нейтральных молекул [16]. Расчет осуществлялся посредством деления соответствующих энтальпий:

(KF) 587500; 419200; (KBr) 373500;

308900.

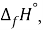
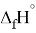
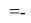
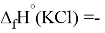
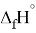
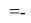
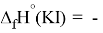
X(Cl) X(F)

(KF) 4 587,5) ;

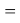
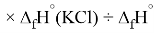
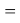
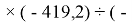
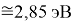
X(Br) X(F) (KF) 4 587,5) ;

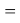
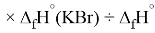
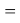
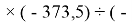
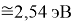
X(I)

X(F) (KF) (KF) 4 587,5) .

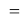
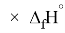
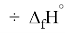
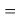
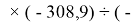
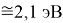
Анализ результатов расчетов показал удовлетворительное совпадение значений ЭО для одних и тех же атомов, рассчитанных различными способами. Наиболее близкими к табличным значениям ЭО были те, которые вычислялись с использованием разности между энергиями диссоциаций соответствующих молекул.

2.3 Алгоритм расчета ЭО по энергиям простых молекул в одном периоде

В настоящей работе также рассматривалась возможность расчета ЭО по энергиям диссоциации простых молекул, состоящих из щелочных металлов и галогенов. Результаты расчета приведены ниже:

D(LiF) 577000

96485,34 5,9802 эВ;

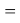
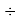
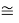
D(NaCl) 412100 96485,34 4,2711 эВ;

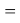
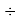
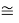
D(KBr) 379100 96485,34 3,9291 эВ;

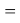
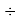
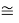
D(RbI)

318800 96485,34 3,3041 эВ.

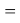
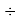
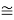
Совершенно очевидно, что энергия диссоциации молекул в два раза больше чем ожидалось. В научной литературе отсутствует рассмотрение этого феномена.

Если X(F) 4,0 эВ а X(Li) 0,975 эВ, то естественно ожидать, что их разница должна быть равной 3,0 эВ.

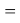
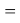
Данный феномен нами был объяснен следующим образом. Должны существовать две ЭО, основанные на разных принципах. Например, ЭО, предложенная Оллредом и Роховым [9] и базирующаяся на энергии ядра атома , и ЭО, предложенная в [10], базирующаяся на энергии электронного облака валентных электронов. В [10] показано, что эти два вида ЭО различаются не более чем на 0,02. Для данного случая энергию диссоциации в первом приближении можно записать в виде уравнения:

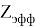
D(A,B) , где

(B) ЭО по Оллреду Рохову, а (B) по [10].

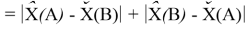
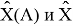
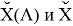
В пределах одного периода энергии диссоциации молекул, содержащих щелочные металлы и галогены, равны удвоенной разности ЭО щелочных металлов и галогенов, входящих в данную молекулу. Если же молекула содержит щелочные металлы и галогены из разных периодов, то значение энергии диссоциации будет равно сумме значений ЭО этих щелочных металлов и галогенов.

Это означает, что суммируются либо вычитаются ЭО (энергии), определяющие кулоновские силы, а следовательно суммируются либо вычитаются два вида ЭО атомов. Таким образом, ЭО это энергия, сложным образом проявляющаяся при организации связей в молекулах.

Таблица 3

Расчет энергии диссоциации простых молекул, состоящих из щелочного металла и галогена

M(A,B)	D(A,B)
M(Li,Cl)	4,861	3,916	0,945
M(Li,Br)	4,341	3,717	0,624
M(Li,I)	3,578	3,168	0,410
M(Li,F)	5,982		0,14
M(Na,F)	4,947	5,025	0,078
M(Na,Br)	3,763	3,767	0,004
M(Na,I)	3,153	3,218	0,065
M(Na,Cl)	4,271		0,39
M(K,F)	5,070	4,909	0,161
M(K,Cl)	4,488	3,850	0,638
M(K,I)	3,342	3,102	0,240
M(K,Br)	3,929		0,225
M(Rb,F)	5,120	4,884	0,236
M(Rb,Cl)	4,432	3,825	0,607
M(Rb,Br)	3,946	3,626	0,320
M(Rb,I)	3,304		0,52

Среднее арифметическое 0,3502.

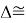
ЭО галогенов в простых молекулах, при атомах одного и того же периода, рассчитывается следующим образом [13]:

X(F)

X(Li) 0,5 D(LiF) 0,975 0,5 5,9801 4,0 эВ;

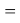
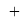
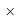
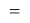
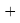
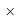
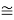
X(Cl) X(Na) 0,5 D(NaCl)

3,16 эВ;

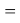
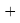
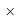
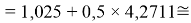
X(Br) X(K) 0,5 D(KBr) 2,87 эВ;

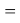
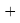
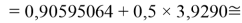
X(I) X(Rb) 0,5 D(RbI) 0,8838542876

0,5 2,54 эВ.

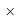
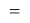
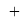
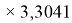
В пределах одного периода энергии ядер и валентных электронов простых молекул суммируются, что равносильно суммированию их ЭО. Это возможно только в том случае, если в молекуле существуют две ЭО, основанные на разных принципах. Если молекула образована атомом щелочного металла из другого периода, то атом щелочного металла потерял электрон и уже не способен отдавать энергию на электронном уровне, а значит отсутствует и ЭО на электронном уровне.

2.4 Дальнейшие направления развития исследования

Основное внимание в настоящей работе было сосредоточено на изучении табличных данных и применении различных методов для их обработки с целью расчета ЭО атомов с повышенной точностью. В справочнике [15] данные более точные, но в нем не в полной мере представлены энергии диссоциации гидридов. В справочнике [17] энергии представлены в большем объеме, однако точность их значений мала. Поэтому требуется создание иных методов обработки «не достаточно точных справочных данных» с целью достижения возможности их достоверного использования.

Расчет более точных значений ЭО атомов несомненно представляет большой интерес, но еще больший интерес имеет физический смысл ЭО атомов. В данной работе показано, что ЭО — энергия, сложным образом проявляющаяся при организации связей в молекулах и имеет размерность в эВ. Однако имеется и неразрешенная по настоящее время проблема. Оллред и Рохов когда постулировали для расчета ЭО атомов свое знаменитое уравнение, то объявили ЭО как «электростатическую силу» (со всеми вытекающими последствиями) [9]. Эта проблема требует разрешения в виде теоретического доказательства.

Определяющим фактором использования в вычислениях значений энергии диссоциации простых молекул — это возможность рассчитать более точные значения ЭО за счет отсутствия в самих вычислениях неточных значений радиусов атомов . Использование этих уточненных значений ЭО, позволит более точно рассчитывать как орбитальные, металлические так и ковалентные радиусы атомов.

Заключение

Материалом для проведенного нами исследования послужили труды выдающихся ученых. К их числу относятся Л. Полинг, А. Оллред, Ю. Рохов, А. Оганов и другие. Всесторонний анализ их трудов позволил сделать следующие выводы:

В связи с отсутствием достаточного количества данных в таблицах энергии диссоциации ни Л. Полинг, ни А. Оллред, ни А. Оганов, ни автор настоящей работы не смогли рассчитать ЭО всех химических элементов таблицы Д. И. Менделеева. В связи с этим, можно считать, что теория Л. Полинга на сегодняшний день — только гипотеза, хотя научные методы, подходы и приемы, которыми пользовался в своей деятельности Л. Полинг, значимы и в настоящее время.

Регрессионный метод обработки эмпирических данных является самым давним. Однако, он очень плодотворен, так как позволяет не только выявлять математические зависимости, но и осуществлять «исправление» эмпирических данных с приемлемой точностью.

По результатам проведенного исследования можно сделать следующие выводы:

Цель исследования достигнута. Гипотеза подтверждена. Впервые достоверно определена область вариабельности значения ЭО X(Na), и тем самым подтверждена гипотеза о значении величины ЭО X(Na) близкой к единице (1,025 эВ).

Расчет ЭО атомов осуществлялся с помощью специально подобранных энергий диссоциаций молекул.

В состав алгоритма расчета ЭО химических элементов первой группы вошли: метод наименьших квадратов, метод последовательных приближений и особенности геометрической прогрессии.

Получены более точные значения ЭО атомов первой группы. Оценить полученную в данной работе точность расчета ЭО не представляется возможным в связи с отсутствием эталона. Однако можно утверждать, что отклонение рассчитанных значений ЭО от приводимых в таблице Оллреда и Рохова составило примерно 0,015.

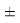
Установлено, что в пределах одного периода энергии диссоциации молекул, содержащих щелочные металлы и галогены, равны удвоенной разности ЭО щелочных металлов и галогенов, входящих в конкретную молекулу. Это означает, что должны существовать две ЭО, основанные на разных принципах. При этом значение энергии диссоциации в первом приближении можно записать в виде уравнения D(A,B) , где (B) ЭО по Оллреду Рохову [9], а (B) ЭО по уравнению из [11]. Если же молекула содержит щелочные металлы и галогены из разных периодов, то значение энергии диссоциации будет равно сумме значений ЭО этих щелочных металлов и галогенов.

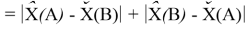
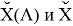
Литература:

1. Электроотрицательность [Электронный ресурс] URL: https://translated.turbopages.org/proxy_u/en-ru.ru.1b5d790b-63e4b987–92f9ce0b-74722d776562/https/en.wikipedia.org/wiki/Mulliken_Scale Загл. с экрана.
2. Бацанов С. С. Электроотрицательность элементов и химическая свяэь. Сибирское отделение АН СССР,1962. 196 с.
3. Еремин В. В., Борщевский А. Я. Основы общей и физической химии: Учебное пособие. Долгопрудный: Издательский Дом «Интеллект», 2018. — 848 с.
4. Полинг Л. Природа химической связи. Москва, Ленинград Государственное научнотехническое издательство химической литературы, 1947. — 438 с.
5. A. L. Allred, J. Inorg. Chem., 17, pp 215 to 221 (1961)
6. Электроотрицательность химических элементов теперь можно считать по-новому [Электронный ресурс] URL: https://www.nkj.ru/news/41317/ Загл. с экрана.
7. Российские химики нашли несоответствие в формуле нобелевского лауреата [Электронный ресурс] URL: https://ria.ru/20210407/elektrootritsatelnost-1727163698.html Загл. с экрана.
8. Tantardini, C., Oganov, A. R. Thermochemical electronegativinies of the elements. Nat Commun 12, 2087 (2021). https:// doi.org/10.1038/ s41467–021–22429–0.
9. A. L. Allred, J. and E. G. Rochow Inorg. Chem., 5, pp 254 to 268 (1958)
10. Рогов Р. Ю. Расчет электроотрицательности химических элементов в таблице Д. И. Менделеева //Международный научный журнал «Юный ученый» № 6 (58), июнь 2022 г. (стр. 92–101) — URL: http://yun/moluch.ru/archive/58/3113/ (ISSN 2409–564X, свидетельство о регистрации СМИ ПИ № ФС77–61102 от 19 марта 2015 г.).
11. Коломиец Л. В., Поникарова Н. Ю. Метод наименьших квадратов: методические указания — Самара., Издательство Самарского университета, 2017. — 32 с.
12. Румшиский Л. З. Математическая обработка результатов эксперимента. М., Наука, 1971, 192 с..
13. Разработка метода расчета эффективного ядра атома / Р. Ю. Рогов // Сборник материалов XIII Международной олимпиады-конкурса научных работ учащихся школ, гимназий, лицеев и колледжей «Химия: наука и искусство» имени В. Я. Курбатова. 22- 23 марта 2023 года. — Санкт-Петербург: Дуит, 2023. — 245 с. — ISBN 978_5_905240_90_4. — С. 108–110.
14. Рогов Р. Ю. Количественная оценка химических элементов в периодах и первой группе таблицы Д. И. Менделеева //Международный научный журнал «Молодой ученый» № 4 (451), январь 2023 г. (стр. 92–101) — URL: http://yun/moluch.ru/archive/58/3113/ (ISSN 2409–564X, свидетельство о регистрации СМИ ПИ № ФС77–61102 от 19 марта 2015 г.).
15. Волков А. И., Жарский И. М. Справочник по общей и неорганической химии. — Минск: Букмастер, 2013. — 224 с.
16. Волков А. И., Жарский И. М. Справочник по физической химии. — Минск: «Литера Гранд» «Книжный дом», 2016. — 400 с.
17. Молекулярные постоянные неорганических соединений: Справочник /К. С. Краснов, Н. В. Филиппенко, В. А. Бобкова и др. Под ред. докт. хим. наук К. С. Краснова — Л.: Химия, 1979. — 448 с.